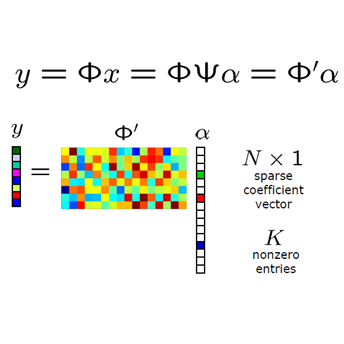
The reconstruction of quantum states from experimental measurements, often achieved using quantum state tomography (QST), is crucial for the verification and benchmarking of quantum devices. However, performing QST for a generic unstructured quantum state requires an enormous number of state copies that grows \emph{exponentially} with the number of individual quanta in the system, even for the most optimal measurement settings. Fortunately, many physical quantum states, such as states generated by noisy, intermediate-scale quantum computers, are usually structured. In one dimension, such states are expected to be well approximated by matrix product operators (MPOs) with a finite matrix/bond dimension independent of the number of qubits, therefore enabling efficient state representation. Nevertheless, it is still unclear whether efficient QST can be performed for these states in general. In this paper, we attempt to bridge this gap and establish theoretical guarantees for the stable recovery of MPOs using tools from compressive sensing and the theory of empirical processes. We begin by studying two types of random measurement settings: Gaussian measurements and Haar random rank-one Positive Operator Valued Measures (POVMs). We show that the information contained in an MPO with a finite bond dimension can be preserved using a number of random measurements that depends only \emph{linearly} on the number of qubits, assuming no statistical error of the measurements. We then study MPO-based QST with physical quantum measurements through Haar random rank-one POVMs that can be implemented on quantum computers. We prove that only a \emph{polynomial} number of state copies in the number of qubits is required to guarantee bounded recovery error of an MPO state.
相關內容
Discrete state spaces represent a major computational challenge to statistical inference, since the computation of normalisation constants requires summation over large or possibly infinite sets, which can be impractical. This paper addresses this computational challenge through the development of a novel generalised Bayesian inference procedure suitable for discrete intractable likelihood. Inspired by recent methodological advances for continuous data, the main idea is to update beliefs about model parameters using a discrete Fisher divergence, in lieu of the problematic intractable likelihood. The result is a generalised posterior that can be sampled from using standard computational tools, such as Markov chain Monte Carlo, circumventing the intractable normalising constant. The statistical properties of the generalised posterior are analysed, with sufficient conditions for posterior consistency and asymptotic normality established. In addition, a novel and general approach to calibration of generalised posteriors is proposed. Applications are presented on lattice models for discrete spatial data and on multivariate models for count data, where in each case the methodology facilitates generalised Bayesian inference at low computational cost.
We present a variational Monte Carlo algorithm for estimating the lowest excited states of a quantum system which is a natural generalization of the estimation of ground states. The method has no free parameters and requires no explicit orthogonalization of the different states, instead transforming the problem of finding excited states of a given system into that of finding the ground state of an expanded system. Expected values of arbitrary observables can be calculated, including off-diagonal expectations between different states such as the transition dipole moment. Although the method is entirely general, it works particularly well in conjunction with recent work on using neural networks as variational Ansatze for many-electron systems, and we show that by combining this method with the FermiNet and Psiformer Ansatze we can accurately recover vertical excitation energies and oscillator strengths on molecules as large as benzene. Beyond the examples on molecules presented here, we expect this technique will be of great interest for applications of variational quantum Monte Carlo to atomic, nuclear and condensed matter physics.
Estimating the state preparation fidelity of highly entangled states on noisy intermediate-scale quantum (NISQ) devices is an important task for benchmarking and application considerations. Unfortunately, exact fidelity measurements quickly become prohibitively expensive, as they scale exponentially as $O(3^N)$ for $N$-qubit states, using full state tomography with measurements in all Pauli bases combinations. However, Somma and others [PhysRevA.74.052302] established that the complexity could be drastically reduced when looking at fidelity lower bounds for states that exhibit symmetries, such as Dicke States and GHZ States. For larger states, these bounds still need to be tight enough to provide reasonable estimations on NISQ devices. For the first time and more than 15 years after the theoretical introduction, we report meaningful lower bounds for the state preparation fidelity of all Dicke States up to $N=10$, and all GHZ states up to $N=20$ on Quantinuum H1 ion-trap systems using efficient implementations of recently proposed scalable circuits for these states. Our achieved lower bounds match or exceed previously reported exact fidelities on superconducting systems for much smaller states. This work provides a path forward to benchmarking entanglement as NISQ devices improve in size and quality.
Knowledge graphs play a vital role in numerous artificial intelligence tasks, yet they frequently face the issue of incompleteness. In this study, we explore utilizing Large Language Models (LLM) for knowledge graph completion. We consider triples in knowledge graphs as text sequences and introduce an innovative framework called Knowledge Graph LLM (KG-LLM) to model these triples. Our technique employs entity and relation descriptions of a triple as prompts and utilizes the response for predictions. Experiments on various benchmark knowledge graphs demonstrate that our method attains state-of-the-art performance in tasks such as triple classification and relation prediction. We also find that fine-tuning relatively smaller models (e.g., LLaMA-7B, ChatGLM-6B) outperforms recent ChatGPT and GPT-4.
Invariant risk minimization (IRM) has recently emerged as a promising alternative for domain generalization. Nevertheless, the loss function is difficult to optimize for nonlinear classifiers and the original optimization objective could fail when pseudo-invariant features and geometric skews exist. Inspired by IRM, in this paper we propose a novel formulation for domain generalization, dubbed invariant information bottleneck (IIB). IIB aims at minimizing invariant risks for nonlinear classifiers and simultaneously mitigating the impact of pseudo-invariant features and geometric skews. Specifically, we first present a novel formulation for invariant causal prediction via mutual information. Then we adopt the variational formulation of the mutual information to develop a tractable loss function for nonlinear classifiers. To overcome the failure modes of IRM, we propose to minimize the mutual information between the inputs and the corresponding representations. IIB significantly outperforms IRM on synthetic datasets, where the pseudo-invariant features and geometric skews occur, showing the effectiveness of proposed formulation in overcoming failure modes of IRM. Furthermore, experiments on DomainBed show that IIB outperforms $13$ baselines by $0.9\%$ on average across $7$ real datasets.
Data in Knowledge Graphs often represents part of the current state of the real world. Thus, to stay up-to-date the graph data needs to be updated frequently. To utilize information from Knowledge Graphs, many state-of-the-art machine learning approaches use embedding techniques. These techniques typically compute an embedding, i.e., vector representations of the nodes as input for the main machine learning algorithm. If a graph update occurs later on -- specifically when nodes are added or removed -- the training has to be done all over again. This is undesirable, because of the time it takes and also because downstream models which were trained with these embeddings have to be retrained if they change significantly. In this paper, we investigate embedding updates that do not require full retraining and evaluate them in combination with various embedding models on real dynamic Knowledge Graphs covering multiple use cases. We study approaches that place newly appearing nodes optimally according to local information, but notice that this does not work well. However, we find that if we continue the training of the old embedding, interleaved with epochs during which we only optimize for the added and removed parts, we obtain good results in terms of typical metrics used in link prediction. This performance is obtained much faster than with a complete retraining and hence makes it possible to maintain embeddings for dynamic Knowledge Graphs.
Text to speech (TTS), or speech synthesis, which aims to synthesize intelligible and natural speech given text, is a hot research topic in speech, language, and machine learning communities and has broad applications in the industry. As the development of deep learning and artificial intelligence, neural network-based TTS has significantly improved the quality of synthesized speech in recent years. In this paper, we conduct a comprehensive survey on neural TTS, aiming to provide a good understanding of current research and future trends. We focus on the key components in neural TTS, including text analysis, acoustic models and vocoders, and several advanced topics, including fast TTS, low-resource TTS, robust TTS, expressive TTS, and adaptive TTS, etc. We further summarize resources related to TTS (e.g., datasets, opensource implementations) and discuss future research directions. This survey can serve both academic researchers and industry practitioners working on TTS.
Causal inference is a critical research topic across many domains, such as statistics, computer science, education, public policy and economics, for decades. Nowadays, estimating causal effect from observational data has become an appealing research direction owing to the large amount of available data and low budget requirement, compared with randomized controlled trials. Embraced with the rapidly developed machine learning area, various causal effect estimation methods for observational data have sprung up. In this survey, we provide a comprehensive review of causal inference methods under the potential outcome framework, one of the well known causal inference framework. The methods are divided into two categories depending on whether they require all three assumptions of the potential outcome framework or not. For each category, both the traditional statistical methods and the recent machine learning enhanced methods are discussed and compared. The plausible applications of these methods are also presented, including the applications in advertising, recommendation, medicine and so on. Moreover, the commonly used benchmark datasets as well as the open-source codes are also summarized, which facilitate researchers and practitioners to explore, evaluate and apply the causal inference methods.
Knowledge graph embedding, which aims to represent entities and relations as low dimensional vectors (or matrices, tensors, etc.), has been shown to be a powerful technique for predicting missing links in knowledge graphs. Existing knowledge graph embedding models mainly focus on modeling relation patterns such as symmetry/antisymmetry, inversion, and composition. However, many existing approaches fail to model semantic hierarchies, which are common in real-world applications. To address this challenge, we propose a novel knowledge graph embedding model---namely, Hierarchy-Aware Knowledge Graph Embedding (HAKE)---which maps entities into the polar coordinate system. HAKE is inspired by the fact that concentric circles in the polar coordinate system can naturally reflect the hierarchy. Specifically, the radial coordinate aims to model entities at different levels of the hierarchy, and entities with smaller radii are expected to be at higher levels; the angular coordinate aims to distinguish entities at the same level of the hierarchy, and these entities are expected to have roughly the same radii but different angles. Experiments demonstrate that HAKE can effectively model the semantic hierarchies in knowledge graphs, and significantly outperforms existing state-of-the-art methods on benchmark datasets for the link prediction task.
Graphs, which describe pairwise relations between objects, are essential representations of many real-world data such as social networks. In recent years, graph neural networks, which extend the neural network models to graph data, have attracted increasing attention. Graph neural networks have been applied to advance many different graph related tasks such as reasoning dynamics of the physical system, graph classification, and node classification. Most of the existing graph neural network models have been designed for static graphs, while many real-world graphs are inherently dynamic. For example, social networks are naturally evolving as new users joining and new relations being created. Current graph neural network models cannot utilize the dynamic information in dynamic graphs. However, the dynamic information has been proven to enhance the performance of many graph analytical tasks such as community detection and link prediction. Hence, it is necessary to design dedicated graph neural networks for dynamic graphs. In this paper, we propose DGNN, a new {\bf D}ynamic {\bf G}raph {\bf N}eural {\bf N}etwork model, which can model the dynamic information as the graph evolving. In particular, the proposed framework can keep updating node information by capturing the sequential information of edges, the time intervals between edges and information propagation coherently. Experimental results on various dynamic graphs demonstrate the effectiveness of the proposed framework.