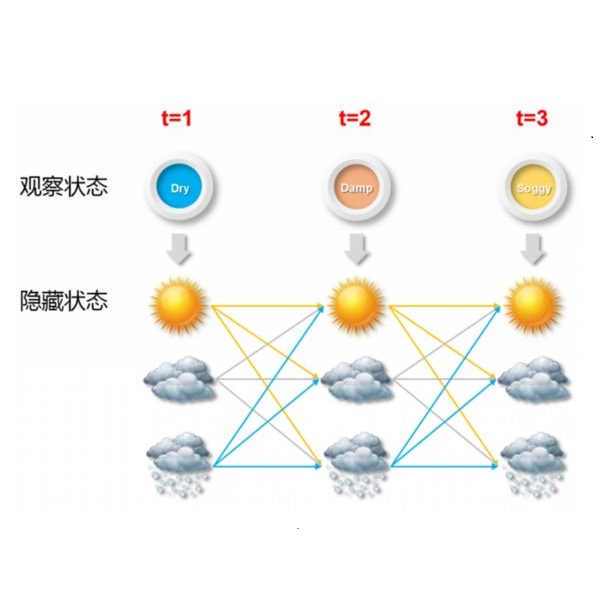
The Continuous-Time Hidden Markov Model (CT-HMM) is an attractive approach to modeling disease progression due to its ability to describe noisy observations arriving irregularly in time. However, the lack of an efficient parameter learning algorithm for CT-HMM restricts its use to very small models or requires unrealistic constraints on the state transitions. In this paper, we present the first complete characterization of efficient EM-based learning methods for CT-HMM models, as well as the first solution to decoding the optimal state transition sequence and the corresponding state dwelling time. We show that EM-based learning consists of two challenges: the estimation of posterior state probabilities and the computation of end-state conditioned statistics. We solve the first challenge by reformulating the estimation problem as an equivalent discrete time-inhomogeneous hidden Markov model. The second challenge is addressed by adapting three distinct approaches from the continuous time Markov chain (CTMC) literature to the CT-HMM domain. Additionally, we further improve the efficiency of the most efficient method by a factor of the number of states. Then, for decoding, we incorporate a state-of-the-art method from the (CTMC) literature, and extend the end-state conditioned optimal state sequence decoding to the CT-HMM case with the computation of the expected state dwelling time. We demonstrate the use of CT-HMMs with more than 100 states to visualize and predict disease progression using a glaucoma dataset and an Alzheimer's disease dataset, and to decode and visualize the most probable state transition trajectory for individuals on the glaucoma dataset, which helps to identify progressing phenotypes in a comprehensive way. Finally, we apply the CT-HMM modeling and decoding strategy to investigate the progression of language acquisition and development.
相關內容
I present a deep reinforcement learning (RL) solution to the mathematical problem known as the Newsvendor model, which seeks to optimize profit given a probabilistic demand distribution. To reflect a more realistic and complex situation, the demand distribution can change for different days of the week, thus changing the optimum behavior. I used a Twin-Delayed Deep Deterministic Policy Gradient agent (written as completely original code) with both an actor and critic network to solve this problem. The agent was able to learn optimal behavior consistent with the analytical solution of the problem, and could identify separate probability distributions for different days of the week and behave accordingly.
Disentanglement is a useful property in representation learning which increases the interpretability of generative models such as Variational Auto-Encoders (VAE), Generative Adversarial Models, and their many variants. Typically in such models, an increase in disentanglement performance is traded-off with generation quality. In the context of latent space models, this work presents a representation learning framework that explicitly promotes disentanglement by encouraging orthogonal directions of variations. The proposed objective is the sum of an auto-encoder error term along with a Principal Component Analysis reconstruction error in the feature space. This has an interpretation of a Restricted Kernel Machine with the eigenvector matrix valued on the Stiefel manifold. Our analysis shows that such a construction promotes disentanglement by matching the principal directions in the latent space with the directions of orthogonal variation in data space. In an alternating minimization scheme, we use Cayley ADAM algorithm -- a stochastic optimization method on the Stiefel manifold along with the ADAM optimizer. Our theoretical discussion and various experiments show that the proposed model improves over many VAE variants in terms of both generation quality and disentangled representation learning.
We study the problem of policy evaluation with linear function approximation and present efficient and practical algorithms that come with strong optimality guarantees. We begin by proving lower bounds that establish baselines on both the deterministic error and stochastic error in this problem. In particular, we prove an oracle complexity lower bound on the deterministic error in an instance-dependent norm associated with the stationary distribution of the transition kernel, and use the local asymptotic minimax machinery to prove an instance-dependent lower bound on the stochastic error in the i.i.d. observation model. Existing algorithms fail to match at least one of these lower bounds: To illustrate, we analyze a variance-reduced variant of temporal difference learning, showing in particular that it fails to achieve the oracle complexity lower bound. To remedy this issue, we develop an accelerated, variance-reduced fast temporal difference algorithm (VRFTD) that simultaneously matches both lower bounds and attains a strong notion of instance-optimality. Finally, we extend the VRFTD algorithm to the setting with Markovian observations, and provide instance-dependent convergence results that match those in the i.i.d. setting up to a multiplicative factor that is proportional to the mixing time of the chain. Our theoretical guarantees of optimality are corroborated by numerical experiments.
In this paper, we propose a multiphysics finite element method for a nonlinear poroelasticity model. To better describe the processes of deformation and diffusion, we firstly reformulate the nonlinear fluid-solid coupling problem into a fluid-fluid coupling problem by a multiphysics approach. Then we design a fully discrete time-stepping scheme to use multiphysics finite element method with $P_2-P_1-P_1$ element pairs for the space variables and backward Euler method for the time variable, and we adopt the Newton iterative method to deal with the nonlinear term. Also, we derive the discrete energy laws and the optimal convergence order error estimates without any assumption on the nonlinear stress-strain relation. Finally, we show some numerical examples to verify the rationality of theoretical analysis and there is no "locking phenomenon".
This dissertation studies a fundamental open challenge in deep learning theory: why do deep networks generalize well even while being overparameterized, unregularized and fitting the training data to zero error? In the first part of the thesis, we will empirically study how training deep networks via stochastic gradient descent implicitly controls the networks' capacity. Subsequently, to show how this leads to better generalization, we will derive {\em data-dependent} {\em uniform-convergence-based} generalization bounds with improved dependencies on the parameter count. Uniform convergence has in fact been the most widely used tool in deep learning literature, thanks to its simplicity and generality. Given its popularity, in this thesis, we will also take a step back to identify the fundamental limits of uniform convergence as a tool to explain generalization. In particular, we will show that in some example overparameterized settings, {\em any} uniform convergence bound will provide only a vacuous generalization bound. With this realization in mind, in the last part of the thesis, we will change course and introduce an {\em empirical} technique to estimate generalization using unlabeled data. Our technique does not rely on any notion of uniform-convergece-based complexity and is remarkably precise. We will theoretically show why our technique enjoys such precision. We will conclude by discussing how future work could explore novel ways to incorporate distributional assumptions in generalization bounds (such as in the form of unlabeled data) and explore other tools to derive bounds, perhaps by modifying uniform convergence or by developing completely new tools altogether.
The Bayesian paradigm has the potential to solve core issues of deep neural networks such as poor calibration and data inefficiency. Alas, scaling Bayesian inference to large weight spaces often requires restrictive approximations. In this work, we show that it suffices to perform inference over a small subset of model weights in order to obtain accurate predictive posteriors. The other weights are kept as point estimates. This subnetwork inference framework enables us to use expressive, otherwise intractable, posterior approximations over such subsets. In particular, we implement subnetwork linearized Laplace: We first obtain a MAP estimate of all weights and then infer a full-covariance Gaussian posterior over a subnetwork. We propose a subnetwork selection strategy that aims to maximally preserve the model's predictive uncertainty. Empirically, our approach is effective compared to ensembles and less expressive posterior approximations over full networks.
Training the generative models with minimal corpus is one of the critical challenges for building open-domain dialogue systems. Existing methods tend to use the meta-learning framework which pre-trains the parameters on all non-target tasks then fine-tunes on the target task. However, fine-tuning distinguishes tasks from the parameter perspective but ignores the model-structure perspective, resulting in similar dialogue models for different tasks. In this paper, we propose an algorithm that can customize a unique dialogue model for each task in the few-shot setting. In our approach, each dialogue model consists of a shared module, a gating module, and a private module. The first two modules are shared among all the tasks, while the third one will differentiate into different network structures to better capture the characteristics of the corresponding task. The extensive experiments on two datasets show that our method outperforms all the baselines in terms of task consistency, response quality, and diversity.
We consider the exploration-exploitation trade-off in reinforcement learning and we show that an agent imbued with a risk-seeking utility function is able to explore efficiently, as measured by regret. The parameter that controls how risk-seeking the agent is can be optimized exactly, or annealed according to a schedule. We call the resulting algorithm K-learning and show that the corresponding K-values are optimistic for the expected Q-values at each state-action pair. The K-values induce a natural Boltzmann exploration policy for which the `temperature' parameter is equal to the risk-seeking parameter. This policy achieves an expected regret bound of $\tilde O(L^{3/2} \sqrt{S A T})$, where $L$ is the time horizon, $S$ is the number of states, $A$ is the number of actions, and $T$ is the total number of elapsed time-steps. This bound is only a factor of $L$ larger than the established lower bound. K-learning can be interpreted as mirror descent in the policy space, and it is similar to other well-known methods in the literature, including Q-learning, soft-Q-learning, and maximum entropy policy gradient, and is closely related to optimism and count based exploration methods. K-learning is simple to implement, as it only requires adding a bonus to the reward at each state-action and then solving a Bellman equation. We conclude with a numerical example demonstrating that K-learning is competitive with other state-of-the-art algorithms in practice.
Deep reinforcement learning has recently shown many impressive successes. However, one major obstacle towards applying such methods to real-world problems is their lack of data-efficiency. To this end, we propose the Bottleneck Simulator: a model-based reinforcement learning method which combines a learned, factorized transition model of the environment with rollout simulations to learn an effective policy from few examples. The learned transition model employs an abstract, discrete (bottleneck) state, which increases sample efficiency by reducing the number of model parameters and by exploiting structural properties of the environment. We provide a mathematical analysis of the Bottleneck Simulator in terms of fixed points of the learned policy, which reveals how performance is affected by four distinct sources of error: an error related to the abstract space structure, an error related to the transition model estimation variance, an error related to the transition model estimation bias, and an error related to the transition model class bias. Finally, we evaluate the Bottleneck Simulator on two natural language processing tasks: a text adventure game and a real-world, complex dialogue response selection task. On both tasks, the Bottleneck Simulator yields excellent performance beating competing approaches.
Stochastic gradient Markov chain Monte Carlo (SGMCMC) has become a popular method for scalable Bayesian inference. These methods are based on sampling a discrete-time approximation to a continuous time process, such as the Langevin diffusion. When applied to distributions defined on a constrained space, such as the simplex, the time-discretisation error can dominate when we are near the boundary of the space. We demonstrate that while current SGMCMC methods for the simplex perform well in certain cases, they struggle with sparse simplex spaces; when many of the components are close to zero. However, most popular large-scale applications of Bayesian inference on simplex spaces, such as network or topic models, are sparse. We argue that this poor performance is due to the biases of SGMCMC caused by the discretization error. To get around this, we propose the stochastic CIR process, which removes all discretization error and we prove that samples from the stochastic CIR process are asymptotically unbiased. Use of the stochastic CIR process within a SGMCMC algorithm is shown to give substantially better performance for a topic model and a Dirichlet process mixture model than existing SGMCMC approaches.