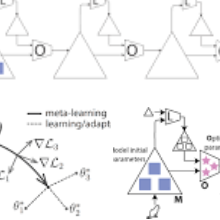
The emerging data-driven methods based on artificial intelligence (AI) have paved the way for intelligent, flexible, and adaptive network management in vehicular applications. To enhance network management towards network automation, this article presents a digital twin (DT) assisted two-tier learning framework, which facilitates the automated life-cycle management of machine learning based intelligent network management functions (INMFs). Specifically, at a high tier, meta learning is employed to capture different levels of general features for the INMFs under nonstationary network conditions. At a low tier, individual learning models are customized for local networks based on fast model adaptation. Hierarchical DTs are deployed at the edge and cloud servers to assist the two-tier learning process, through closed-loop interactions with the physical network domain. Finally, a case study demonstrates the fast and accurate model adaptation ability of meta learning in comparison with benchmark schemes.
相關內容
Gaussian processes (GPs) are commonly used for prediction and inference for spatial data analyses. However, since estimation and prediction tasks have cubic time and quadratic memory complexity in number of locations, GPs are difficult to scale to large spatial datasets. The Vecchia approximation induces sparsity in the dependence structure and is one of several methods proposed to scale GP inference. Our work adds to the substantial research in this area by developing a stochastic gradient Markov chain Monte Carlo (SGMCMC) framework for efficient computation in GPs. At each step, the algorithm subsamples a minibatch of locations and subsequently updates process parameters through a Vecchia-approximated GP likelihood. Since the Vecchia-approximated GP has a time complexity that is linear in the number of locations, this results in scalable estimation in GPs. Through simulation studies, we demonstrate that SGMCMC is competitive with state-of-the-art scalable GP algorithms in terms of computational time and parameter estimation. An application of our method is also provided using the Argo dataset of ocean temperature measurements.
When deploying deep neural networks on robots or other physical systems, the learned model should reliably quantify predictive uncertainty. A reliable uncertainty allows downstream modules to reason about the safety of its actions. In this work, we address metrics for evaluating such an uncertainty. Specifically, we focus on regression tasks, and investigate Area Under Sparsification Error (AUSE), Calibration Error, Spearman's Rank Correlation, and Negative Log-Likelihood (NLL). Using synthetic regression datasets, we look into how those metrics behave under four typical types of uncertainty, their stability regarding the size of the test set, and reveal their strengths and weaknesses. Our results indicate that Calibration Error is the most stable and interpretable metric, but AUSE and NLL also have their respective use cases. We discourage the usage of Spearman's Rank Correlation for evaluating uncertainties and recommend replacing it with AUSE.
Autonomous driving perception models are typically composed of multiple functional modules that interact through complex relationships to accomplish environment understanding. However, perception models are predominantly optimized as a black box through end-to-end training, lacking independent evaluation of functional modules, which poses difficulties for interpretability and optimization. Pioneering in the issue, we propose an evaluation method based on feature map analysis to gauge the convergence of model, thereby assessing functional modules' training maturity. We construct a quantitative metric named as the Feature Map Convergence Score (FMCS) and develop Feature Map Convergence Evaluation Network (FMCE-Net) to measure and predict the convergence degree of models respectively. FMCE-Net achieves remarkable predictive accuracy for FMCS across multiple image classification experiments, validating the efficacy and robustness of the introduced approach. To the best of our knowledge, this is the first independent evaluation method for functional modules, offering a new paradigm for the training assessment towards perception models.
In temporal extensions of Answer Set Programming (ASP) based on linear-time, the behavior of dynamic systems is captured by sequences of states. While this representation reflects their relative order, it abstracts away the specific times associated with each state. However, timing constraints are important in many applications like, for instance, when planning and scheduling go hand in hand. We address this by developing a metric extension of linear-time temporal equilibrium logic, in which temporal operators are constrained by intervals over natural numbers. The resulting Metric Equilibrium Logic provides the foundation of an ASP-based approach for specifying qualitative and quantitative dynamic constraints. To this end, we define a translation of metric formulas into monadic first-order formulas and give a correspondence between their models in Metric Equilibrium Logic and Monadic Quantified Equilibrium Logic, respectively. Interestingly, our translation provides a blue print for implementation in terms of ASP modulo difference constraints.
The adaptive processing of structured data is a long-standing research topic in machine learning that investigates how to automatically learn a mapping from a structured input to outputs of various nature. Recently, there has been an increasing interest in the adaptive processing of graphs, which led to the development of different neural network-based methodologies. In this thesis, we take a different route and develop a Bayesian Deep Learning framework for graph learning. The dissertation begins with a review of the principles over which most of the methods in the field are built, followed by a study on graph classification reproducibility issues. We then proceed to bridge the basic ideas of deep learning for graphs with the Bayesian world, by building our deep architectures in an incremental fashion. This framework allows us to consider graphs with discrete and continuous edge features, producing unsupervised embeddings rich enough to reach the state of the art on several classification tasks. Our approach is also amenable to a Bayesian nonparametric extension that automatizes the choice of almost all model's hyper-parameters. Two real-world applications demonstrate the efficacy of deep learning for graphs. The first concerns the prediction of information-theoretic quantities for molecular simulations with supervised neural models. After that, we exploit our Bayesian models to solve a malware-classification task while being robust to intra-procedural code obfuscation techniques. We conclude the dissertation with an attempt to blend the best of the neural and Bayesian worlds together. The resulting hybrid model is able to predict multimodal distributions conditioned on input graphs, with the consequent ability to model stochasticity and uncertainty better than most works. Overall, we aim to provide a Bayesian perspective into the articulated research field of deep learning for graphs.
Contrastive learning models have achieved great success in unsupervised visual representation learning, which maximize the similarities between feature representations of different views of the same image, while minimize the similarities between feature representations of views of different images. In text summarization, the output summary is a shorter form of the input document and they have similar meanings. In this paper, we propose a contrastive learning model for supervised abstractive text summarization, where we view a document, its gold summary and its model generated summaries as different views of the same mean representation and maximize the similarities between them during training. We improve over a strong sequence-to-sequence text generation model (i.e., BART) on three different summarization datasets. Human evaluation also shows that our model achieves better faithfulness ratings compared to its counterpart without contrastive objectives.
Recent contrastive representation learning methods rely on estimating mutual information (MI) between multiple views of an underlying context. E.g., we can derive multiple views of a given image by applying data augmentation, or we can split a sequence into views comprising the past and future of some step in the sequence. Contrastive lower bounds on MI are easy to optimize, but have a strong underestimation bias when estimating large amounts of MI. We propose decomposing the full MI estimation problem into a sum of smaller estimation problems by splitting one of the views into progressively more informed subviews and by applying the chain rule on MI between the decomposed views. This expression contains a sum of unconditional and conditional MI terms, each measuring modest chunks of the total MI, which facilitates approximation via contrastive bounds. To maximize the sum, we formulate a contrastive lower bound on the conditional MI which can be approximated efficiently. We refer to our general approach as Decomposed Estimation of Mutual Information (DEMI). We show that DEMI can capture a larger amount of MI than standard non-decomposed contrastive bounds in a synthetic setting, and learns better representations in a vision domain and for dialogue generation.
Edge intelligence refers to a set of connected systems and devices for data collection, caching, processing, and analysis in locations close to where data is captured based on artificial intelligence. The aim of edge intelligence is to enhance the quality and speed of data processing and protect the privacy and security of the data. Although recently emerged, spanning the period from 2011 to now, this field of research has shown explosive growth over the past five years. In this paper, we present a thorough and comprehensive survey on the literature surrounding edge intelligence. We first identify four fundamental components of edge intelligence, namely edge caching, edge training, edge inference, and edge offloading, based on theoretical and practical results pertaining to proposed and deployed systems. We then aim for a systematic classification of the state of the solutions by examining research results and observations for each of the four components and present a taxonomy that includes practical problems, adopted techniques, and application goals. For each category, we elaborate, compare and analyse the literature from the perspectives of adopted techniques, objectives, performance, advantages and drawbacks, etc. This survey article provides a comprehensive introduction to edge intelligence and its application areas. In addition, we summarise the development of the emerging research field and the current state-of-the-art and discuss the important open issues and possible theoretical and technical solutions.
Embedding entities and relations into a continuous multi-dimensional vector space have become the dominant method for knowledge graph embedding in representation learning. However, most existing models ignore to represent hierarchical knowledge, such as the similarities and dissimilarities of entities in one domain. We proposed to learn a Domain Representations over existing knowledge graph embedding models, such that entities that have similar attributes are organized into the same domain. Such hierarchical knowledge of domains can give further evidence in link prediction. Experimental results show that domain embeddings give a significant improvement over the most recent state-of-art baseline knowledge graph embedding models.
Graph neural networks (GNNs) are a popular class of machine learning models whose major advantage is their ability to incorporate a sparse and discrete dependency structure between data points. Unfortunately, GNNs can only be used when such a graph-structure is available. In practice, however, real-world graphs are often noisy and incomplete or might not be available at all. With this work, we propose to jointly learn the graph structure and the parameters of graph convolutional networks (GCNs) by approximately solving a bilevel program that learns a discrete probability distribution on the edges of the graph. This allows one to apply GCNs not only in scenarios where the given graph is incomplete or corrupted but also in those where a graph is not available. We conduct a series of experiments that analyze the behavior of the proposed method and demonstrate that it outperforms related methods by a significant margin.