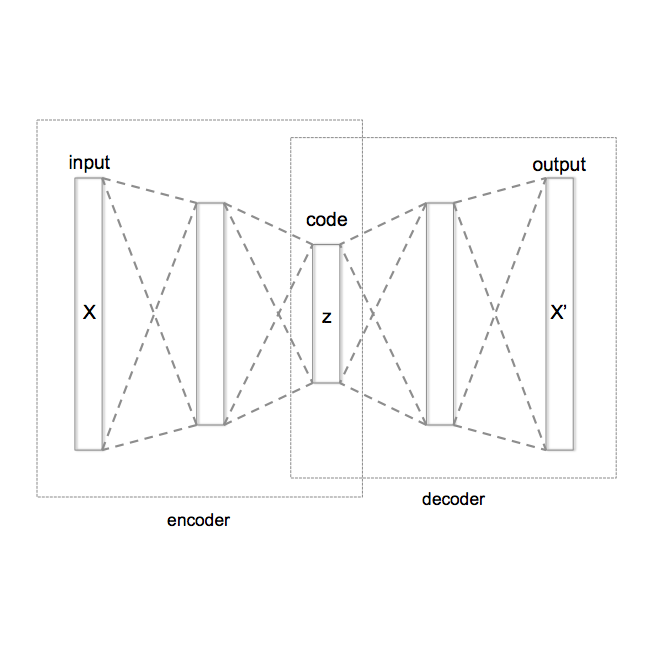
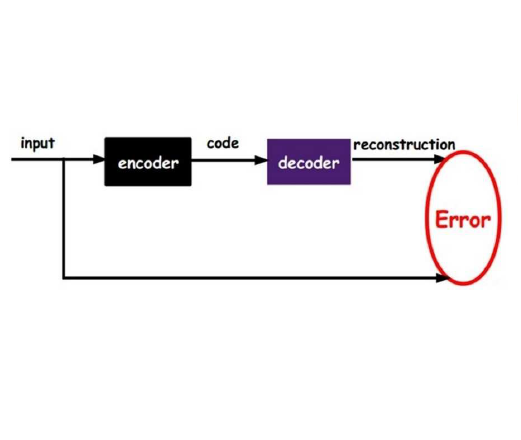
We introduce a method combining variational autoencoders (VAEs) and deep metric learning to perform Bayesian optimisation (BO) over high-dimensional and structured input spaces. By adapting ideas from deep metric learning, we use label guidance from the blackbox function to structure the VAE latent space, facilitating the Gaussian process fit and yielding improved BO performance. Importantly for BO problem settings, our method operates in semi-supervised regimes where only few labelled data points are available. We run experiments on three real-world tasks, achieving state-of-the-art results on the penalised logP molecule generation benchmark using just 3% of the labelled data required by previous approaches. As a theoretical contribution, we present a proof of vanishing regret for VAE BO.
相關內容
The last decade has witnessed an experimental revolution in data science and machine learning, epitomised by deep learning methods. Indeed, many high-dimensional learning tasks previously thought to be beyond reach -- such as computer vision, playing Go, or protein folding -- are in fact feasible with appropriate computational scale. Remarkably, the essence of deep learning is built from two simple algorithmic principles: first, the notion of representation or feature learning, whereby adapted, often hierarchical, features capture the appropriate notion of regularity for each task, and second, learning by local gradient-descent type methods, typically implemented as backpropagation. While learning generic functions in high dimensions is a cursed estimation problem, most tasks of interest are not generic, and come with essential pre-defined regularities arising from the underlying low-dimensionality and structure of the physical world. This text is concerned with exposing these regularities through unified geometric principles that can be applied throughout a wide spectrum of applications. Such a 'geometric unification' endeavour, in the spirit of Felix Klein's Erlangen Program, serves a dual purpose: on one hand, it provides a common mathematical framework to study the most successful neural network architectures, such as CNNs, RNNs, GNNs, and Transformers. On the other hand, it gives a constructive procedure to incorporate prior physical knowledge into neural architectures and provide principled way to build future architectures yet to be invented.
Approaches based on deep neural networks have achieved striking performance when testing data and training data share similar distribution, but can significantly fail otherwise. Therefore, eliminating the impact of distribution shifts between training and testing data is crucial for building performance-promising deep models. Conventional methods assume either the known heterogeneity of training data (e.g. domain labels) or the approximately equal capacities of different domains. In this paper, we consider a more challenging case where neither of the above assumptions holds. We propose to address this problem by removing the dependencies between features via learning weights for training samples, which helps deep models get rid of spurious correlations and, in turn, concentrate more on the true connection between discriminative features and labels. Extensive experiments clearly demonstrate the effectiveness of our method on multiple distribution generalization benchmarks compared with state-of-the-art counterparts. Through extensive experiments on distribution generalization benchmarks including PACS, VLCS, MNIST-M, and NICO, we show the effectiveness of our method compared with state-of-the-art counterparts.
This paper presents a hardness-aware deep metric learning (HDML) framework. Most previous deep metric learning methods employ the hard negative mining strategy to alleviate the lack of informative samples for training. However, this mining strategy only utilizes a subset of training data, which may not be enough to characterize the global geometry of the embedding space comprehensively. To address this problem, we perform linear interpolation on embeddings to adaptively manipulate their hard levels and generate corresponding label-preserving synthetics for recycled training, so that information buried in all samples can be fully exploited and the metric is always challenged with proper difficulty. Our method achieves very competitive performance on the widely used CUB-200-2011, Cars196, and Stanford Online Products datasets.
Deep learning is the mainstream technique for many machine learning tasks, including image recognition, machine translation, speech recognition, and so on. It has outperformed conventional methods in various fields and achieved great successes. Unfortunately, the understanding on how it works remains unclear. It has the central importance to lay down the theoretic foundation for deep learning. In this work, we give a geometric view to understand deep learning: we show that the fundamental principle attributing to the success is the manifold structure in data, namely natural high dimensional data concentrates close to a low-dimensional manifold, deep learning learns the manifold and the probability distribution on it. We further introduce the concepts of rectified linear complexity for deep neural network measuring its learning capability, rectified linear complexity of an embedding manifold describing the difficulty to be learned. Then we show for any deep neural network with fixed architecture, there exists a manifold that cannot be learned by the network. Finally, we propose to apply optimal mass transportation theory to control the probability distribution in the latent space.
Large margin nearest neighbor (LMNN) is a metric learner which optimizes the performance of the popular $k$NN classifier. However, its resulting metric relies on pre-selected target neighbors. In this paper, we address the feasibility of LMNN's optimization constraints regarding these target points, and introduce a mathematical measure to evaluate the size of the feasible region of the optimization problem. We enhance the optimization framework of LMNN by a weighting scheme which prefers data triplets which yield a larger feasible region. This increases the chances to obtain a good metric as the solution of LMNN's problem. We evaluate the performance of the resulting feasibility-based LMNN algorithm using synthetic and real datasets. The empirical results show an improved accuracy for different types of datasets in comparison to regular LMNN.

Deep metric learning has been demonstrated to be highly effective in learning semantic representation and encoding information that can be used to measure data similarity, by relying on the embedding learned from metric learning. At the same time, variational autoencoder (VAE) has widely been used to approximate inference and proved to have a good performance for directed probabilistic models. However, for traditional VAE, the data label or feature information are intractable. Similarly, traditional representation learning approaches fail to represent many salient aspects of the data. In this project, we propose a novel integrated framework to learn latent embedding in VAE by incorporating deep metric learning. The features are learned by optimizing a triplet loss on the mean vectors of VAE in conjunction with standard evidence lower bound (ELBO) of VAE. This approach, which we call Triplet based Variational Autoencoder (TVAE), allows us to capture more fine-grained information in the latent embedding. Our model is tested on MNIST data set and achieves a high triplet accuracy of 95.60% while the traditional VAE (Kingma & Welling, 2013) achieves triplet accuracy of 75.08%.
Clustering and classification critically rely on distance metrics that provide meaningful comparisons between data points. We present mixed-integer optimization approaches to find optimal distance metrics that generalize the Mahalanobis metric extensively studied in the literature. Additionally, we generalize and improve upon leading methods by removing reliance on pre-designated "target neighbors," "triplets," and "similarity pairs." Another salient feature of our method is its ability to enable active learning by recommending precise regions to sample after an optimal metric is computed to improve classification performance. This targeted acquisition can significantly reduce computational burden by ensuring training data completeness, representativeness, and economy. We demonstrate classification and computational performance of the algorithms through several simple and intuitive examples, followed by results on real image and medical datasets.
Zero shot learning in Image Classification refers to the setting where images from some novel classes are absent in the training data but other information such as natural language descriptions or attribute vectors of the classes are available. This setting is important in the real world since one may not be able to obtain images of all the possible classes at training. While previous approaches have tried to model the relationship between the class attribute space and the image space via some kind of a transfer function in order to model the image space correspondingly to an unseen class, we take a different approach and try to generate the samples from the given attributes, using a conditional variational autoencoder, and use the generated samples for classification of the unseen classes. By extensive testing on four benchmark datasets, we show that our model outperforms the state of the art, particularly in the more realistic generalized setting, where the training classes can also appear at the test time along with the novel classes.
We propose an Active Learning approach to image segmentation that exploits geometric priors to streamline the annotation process. We demonstrate this for both background-foreground and multi-class segmentation tasks in 2D images and 3D image volumes. Our approach combines geometric smoothness priors in the image space with more traditional uncertainty measures to estimate which pixels or voxels are most in need of annotation. For multi-class settings, we additionally introduce two novel criteria for uncertainty. In the 3D case, we use the resulting uncertainty measure to show the annotator voxels lying on the same planar patch, which makes batch annotation much easier than if they were randomly distributed in the volume. The planar patch is found using a branch-and-bound algorithm that finds a patch with the most informative instances. We evaluate our approach on Electron Microscopy and Magnetic Resonance image volumes, as well as on regular images of horses and faces. We demonstrate a substantial performance increase over state-of-the-art approaches.
Learning similarity functions between image pairs with deep neural networks yields highly correlated activations of embeddings. In this work, we show how to improve the robustness of such embeddings by exploiting the independence within ensembles. To this end, we divide the last embedding layer of a deep network into an embedding ensemble and formulate training this ensemble as an online gradient boosting problem. Each learner receives a reweighted training sample from the previous learners. Further, we propose two loss functions which increase the diversity in our ensemble. These loss functions can be applied either for weight initialization or during training. Together, our contributions leverage large embedding sizes more effectively by significantly reducing correlation of the embedding and consequently increase retrieval accuracy of the embedding. Our method works with any differentiable loss function and does not introduce any additional parameters during test time. We evaluate our metric learning method on image retrieval tasks and show that it improves over state-of-the-art methods on the CUB 200-2011, Cars-196, Stanford Online Products, In-Shop Clothes Retrieval and VehicleID datasets.