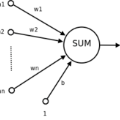
Weather is one of the main problems in implementing forecasts for photovoltaic panel systems. Since it is the main generator of disturbances and interruptions in electrical energy. It is necessary to choose a reliable forecasting model for better energy use. A measurement prototype was constructed in this work, which collects in-situ voltage and current measurements and the environmental factors of radiation, temperature, and humidity. Subsequently, a correlation analysis of the variables and the implementation of artificial neural networks were performed to perform the system forecast. The best estimate was the one made with three variables (lighting, temperature, and humidity), obtaining an error of 0.255. These results show that it is possible to make a good estimate for a photovoltaic panel system.
相關內容
We describe a family of iterative algorithms that involve the repeated execution of discrete and inverse discrete Fourier transforms. One interesting member of this family is motivated by the discrete Fourier transform uncertainty principle and involves the application of a sparsification operation to both the time domain and frequency domain data with convergence obtained when time domain sparsity hits a stable pattern. This sparsification variant has practical utility for signal denoising, in particular the recovery of a periodic spike signal in the presence of Gaussian noise. General convergence properties and denoising performance are demonstrated using simulation studies. We are not aware of prior work on such iterative Fourier transformation algorithms and have written this paper in part to solicit feedback from others in the field who may be familiar with similar techniques.
The problem Power Dominating Set (PDS) is motivated by the placement of phasor measurement units to monitor electrical networks. It asks for a minimum set of vertices in a graph that observes all remaining vertices by exhaustively applying two observation rules. Our contribution is twofold. First, we determine the parameterized complexity of PDS by proving it is $W[P]$-complete when parameterized with respect to the solution size. We note that it was only known to be $W[2]$-hard before. Our second and main contribution is a new algorithm for PDS that efficiently solves practical instances. Our algorithm consists of two complementary parts. The first is a set of reduction rules for PDS that can also be used in conjunction with previously existing algorithms. The second is an algorithm for solving the remaining kernel based on the implicit hitting set approach. Our evaluation on a set of power grid instances from the literature shows that our solver outperforms previous state-of-the-art solvers for PDS by more than one order of magnitude on average. Furthermore, our algorithm can solve previously unsolved instances of continental scale within a few minutes.
The One-versus-One (OvO) strategy is an approach of multi-classification models which focuses on training binary classifiers between each pair of classes. While the OvO strategy takes advantage of balanced training data, the classification accuracy is usually hindered by the voting mechanism to combine all binary classifiers. In this paper, a novel OvO multi-classification model incorporating a joint probability measure is proposed under the deep learning framework. In the proposed model, a two-stage algorithm is developed to estimate the class probability from the pairwise binary classifiers. Given the binary classifiers, the pairwise probability estimate is calibrated by a distance measure on the separating feature hyperplane. From that, the class probability of the subject is estimated by solving a joint probability-based distance minimization problem. Numerical experiments in different applications show that the proposed model achieves generally higher classification accuracy than other state-of-the-art models.
Learning to control unknown nonlinear dynamical systems is a fundamental problem in reinforcement learning and control theory. A commonly applied approach is to first explore the environment (exploration), learn an accurate model of it (system identification), and then compute an optimal controller with the minimum cost on this estimated system (policy optimization). While existing work has shown that it is possible to learn a uniformly good model of the system~\citep{mania2020active}, in practice, if we aim to learn a good controller with a low cost on the actual system, certain system parameters may be significantly more critical than others, and we therefore ought to focus our exploration on learning such parameters. In this work, we consider the setting of nonlinear dynamical systems and seek to formally quantify, in such settings, (a) which parameters are most relevant to learning a good controller, and (b) how we can best explore so as to minimize uncertainty in such parameters. Inspired by recent work in linear systems~\citep{wagenmaker2021task}, we show that minimizing the controller loss in nonlinear systems translates to estimating the system parameters in a particular, task-dependent metric. Motivated by this, we develop an algorithm able to efficiently explore the system to reduce uncertainty in this metric, and prove a lower bound showing that our approach learns a controller at a near-instance-optimal rate. Our algorithm relies on a general reduction from policy optimization to optimal experiment design in arbitrary systems, and may be of independent interest. We conclude with experiments demonstrating the effectiveness of our method in realistic nonlinear robotic systems.
The combinatorial pure exploration (CPE) in the stochastic multi-armed bandit setting (MAB) is a well-studied online decision-making problem: A player wants to find the optimal \emph{action} $\boldsymbol{\pi}^*$ from \emph{action class} $\mathcal{A}$, which is a collection of subsets of arms with certain combinatorial structures. Though CPE can represent many combinatorial structures such as paths, matching, and spanning trees, most existing works focus only on binary action class $\mathcal{A}\subseteq\{0, 1\}^d$ for some positive integer $d$. This binary formulation excludes important problems such as the optimal transport, knapsack, and production planning problems. To overcome this limitation, we extend the binary formulation to real, $\mathcal{A}\subseteq\mathbb{R}^d$, and propose a new algorithm. The only assumption we make is that the number of actions in $\mathcal{A}$ is polynomial in $d$. We show an upper bound of the sample complexity for our algorithm and the action class-dependent lower bound for R-CPE-MAB, by introducing a quantity that characterizes the problem's difficulty, which is a generalization of the notion \emph{width} introduced in Chen et al.[2014].
Real-world software applications must constantly evolve to remain relevant. This evolution occurs when developing new applications or adapting existing ones to meet new requirements, make corrections, or incorporate future functionality. Traditional methods of software quality control involve software quality models and continuous code inspection tools. These measures focus on directly assessing the quality of the software. However, there is a strong correlation and causation between the quality of the development process and the resulting software product. Therefore, improving the development process indirectly improves the software product, too. To achieve this, effective learning from past processes is necessary, often embraced through post mortem organizational learning. While qualitative evaluation of large artifacts is common, smaller quantitative changes captured by application lifecycle management are often overlooked. In addition to software metrics, these smaller changes can reveal complex phenomena related to project culture and management. Leveraging these changes can help detect and address such complex issues. Software evolution was previously measured by the size of changes, but the lack of consensus on a reliable and versatile quantification method prevents its use as a dependable metric. Different size classifications fail to reliably describe the nature of evolution. While application lifecycle management data is rich, identifying which artifacts can model detrimental managerial practices remains uncertain. Approaches such as simulation modeling, discrete events simulation, or Bayesian networks have only limited ability to exploit continuous-time process models of such phenomena. Even worse, the accessibility and mechanistic insight into such gray- or black-box models are typically very low. To address these challenges, we suggest leveraging objectively [...]
Associative memories are devices storing information that can be fully retrieved given partial disclosure of it. We examine a toy model of associative memory and the ultimate limitations it is subjected to within the framework of general probabilistic theories (GPTs), which represent the most general class of physical theories satisfying some basic operational axioms. We ask ourselves how large the dimension of a GPT should be so that it can accommodate $2^m$ states with the property that any $N$ of them are perfectly distinguishable. Call $d(N,m)$ the minimal such dimension. Invoking an old result by Danzer and Gr\"unbaum, we prove that $d(2,m)=m+1$, to be compared with $O(2^m)$ when the GPT is required to be either classical or quantum. This yields an example of a task where GPTs outperform both classical and quantum theory exponentially. More generally, we resolve the case of fixed $N$ and asymptotically large $m$, proving that $d(N,m) \leq m^{1+o_N(1)}$ (as $m\to\infty$) for every $N\geq 2$, which yields again an exponential improvement over classical and quantum theories. Finally, we develop a numerical approach to the general problem of finding the largest $N$-wise mutually distinguishable set for a given GPT, which can be seen as an instance of the maximum clique problem on $N$-regular hypergraphs.
We study the Electrical Impedance Tomography Bayesian inverse problem for recovering the conductivity given noisy measurements of the voltage on some boundary surface electrodes. The uncertain conductivity depends linearly on a countable number of uniformly distributed random parameters in a compact interval, with the coefficient functions in the linear expansion decaying at an algebraic rate. We analyze the surrogate Markov Chain Monte Carlo (MCMC) approach for sampling the posterior probability measure, where the multivariate sparse adaptive interpolation, with interpolating points chosen according to a lower index set, is used for approximating the forward map. The forward equation is approximated once before running the MCMC for all the realizations, using interpolation on the finite element (FE) approximation at the parametric interpolating points. When evaluation of the solution is needed for a realization, we only need to compute a polynomial, thus cutting drastically the computation time. We contribute a rigorous error estimate for the MCMC convergence. In particular, we show that there is a nested sequence of interpolating lower index sets for which we can derive an interpolation error estimate in terms of the cardinality of these sets, uniformly for all the parameter realizations. An explicit convergence rate for the MCMC sampling of the posterior expectation of the conductivity is rigorously derived, in terms of the interpolating point number, the accuracy of the FE approximation of the forward equation, and the MCMC sample number. We perform numerical experiments using an adaptive greedy approach to construct the sets of interpolation points. We show the benefits of this approach over the simple MCMC where the forward equation is repeatedly solved for all the samples and the non-adaptive surrogate MCMC with an isotropic index set treating all the random parameters equally.
Graph Neural Networks (GNNs) are information processing architectures for signals supported on graphs. They are presented here as generalizations of convolutional neural networks (CNNs) in which individual layers contain banks of graph convolutional filters instead of banks of classical convolutional filters. Otherwise, GNNs operate as CNNs. Filters are composed with pointwise nonlinearities and stacked in layers. It is shown that GNN architectures exhibit equivariance to permutation and stability to graph deformations. These properties provide a measure of explanation respecting the good performance of GNNs that can be observed empirically. It is also shown that if graphs converge to a limit object, a graphon, GNNs converge to a corresponding limit object, a graphon neural network. This convergence justifies the transferability of GNNs across networks with different number of nodes.
High spectral dimensionality and the shortage of annotations make hyperspectral image (HSI) classification a challenging problem. Recent studies suggest that convolutional neural networks can learn discriminative spatial features, which play a paramount role in HSI interpretation. However, most of these methods ignore the distinctive spectral-spatial characteristic of hyperspectral data. In addition, a large amount of unlabeled data remains an unexploited gold mine for efficient data use. Therefore, we proposed an integration of generative adversarial networks (GANs) and probabilistic graphical models for HSI classification. Specifically, we used a spectral-spatial generator and a discriminator to identify land cover categories of hyperspectral cubes. Moreover, to take advantage of a large amount of unlabeled data, we adopted a conditional random field to refine the preliminary classification results generated by GANs. Experimental results obtained using two commonly studied datasets demonstrate that the proposed framework achieved encouraging classification accuracy using a small number of data for training.