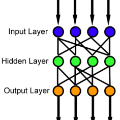
Theoretical understanding of the behavior of infinitely-wide neural networks has been rapidly developed for various architectures due to the celebrated mean-field theory. However, there is a lack of a clear, intuitive framework for extending our understanding to finite networks that are of more practical and realistic importance. In the present contribution, we demonstrate that the behavior of properly initialized neural networks can be understood in terms of universal critical phenomena in absorbing phase transitions. More specifically, we study the order-to-chaos transition in the fully-connected feedforward neural networks and the convolutional ones to show that (i) there is a well-defined transition from the ordered state to the chaotics state even for the finite networks, and (ii) difference in architecture is reflected in that of the universality class of the transition. Remarkably, the finite-size scaling can also be successfully applied, indicating that intuitive phenomenological argument could lead us to semi-quantitative description of the signal propagation dynamics.
相關內容
Physics informed neural network (PINN) approach in Bayesian formulation is presented. We adopt the Bayesian neural network framework formulated by MacKay (Neural Computation 4 (3) (1992) 448). The posterior densities are obtained from Laplace approximation. For each model (fit), the so-called evidence is computed. It is a measure that classifies the hypothesis. The most optimal solution has the maximal value of the evidence. The Bayesian framework allows us to control the impact of the boundary contribution to the total loss. Indeed, the relative weights of loss components are fine-tuned by the Bayesian algorithm. We solve heat, wave, and Burger's equations. The obtained results are in good agreement with the exact solutions. All solutions are provided with the uncertainties computed within the Bayesian framework.
Most existing classical artificial neural networks (ANN) are designed as a tree structure to imitate neural networks. In this paper, we argue that the connectivity of a tree is not sufficient to characterize a neural network. The nodes of the same level of a tree cannot be connected with each other, i.e., these neural unit cannot share information with each other, which is a major drawback of ANN. Although ANN has been significantly improved in recent years to more complex structures, such as the directed acyclic graph (DAG), these methods also have unidirectional and acyclic bias for ANN. In this paper, we propose a method to build a bidirectional complete graph for the nodes in the same level of an ANN, which yokes the nodes of the same level to formulate a neural module. We call our model as YNN in short. YNN promotes the information transfer significantly which obviously helps in improving the performance of the method. Our YNN can imitate neural networks much better compared with the traditional ANN. In this paper, we analyze the existing structural bias of ANN and propose a model YNN to efficiently eliminate such structural bias. In our model, nodes also carry out aggregation and transformation of features, and edges determine the flow of information. We further impose auxiliary sparsity constraint to the distribution of connectedness, which promotes the learned structure to focus on critical connections. Finally, based on the optimized structure, we also design small neural module structure based on the minimum cut technique to reduce the computational burden of the YNN model. This learning process is compatible with the existing networks and different tasks. The obtained quantitative experimental results reflect that the learned connectivity is superior to the traditional NN structure.
Critical learning periods are periods early in development where temporary sensory deficits can have a permanent effect on behavior and learned representations. Despite the radical differences between biological and artificial networks, critical learning periods have been empirically observed in both systems. This suggests that critical periods may be fundamental to learning and not an accident of biology. Yet, why exactly critical periods emerge in deep networks is still an open question, and in particular it is unclear whether the critical periods observed in both systems depend on particular architectural or optimization details. To isolate the key underlying factors, we focus on deep linear network models, and show that, surprisingly, such networks also display much of the behavior seen in biology and artificial networks, while being amenable to analytical treatment. We show that critical periods depend on the depth of the model and structure of the data distribution. We also show analytically and in simulations that the learning of features is tied to competition between sources. Finally, we extend our analysis to multi-task learning to show that pre-training on certain tasks can damage the transfer performance on new tasks, and show how this depends on the relationship between tasks and the duration of the pre-training stage. To the best of our knowledge, our work provides the first analytically tractable model that sheds light into why critical learning periods emerge in biological and artificial networks.
We consider the problem of explaining the predictions of graph neural networks (GNNs), which otherwise are considered as black boxes. Existing methods invariably focus on explaining the importance of graph nodes or edges but ignore the substructures of graphs, which are more intuitive and human-intelligible. In this work, we propose a novel method, known as SubgraphX, to explain GNNs by identifying important subgraphs. Given a trained GNN model and an input graph, our SubgraphX explains its predictions by efficiently exploring different subgraphs with Monte Carlo tree search. To make the tree search more effective, we propose to use Shapley values as a measure of subgraph importance, which can also capture the interactions among different subgraphs. To expedite computations, we propose efficient approximation schemes to compute Shapley values for graph data. Our work represents the first attempt to explain GNNs via identifying subgraphs explicitly and directly. Experimental results show that our SubgraphX achieves significantly improved explanations, while keeping computations at a reasonable level.
The Bayesian paradigm has the potential to solve core issues of deep neural networks such as poor calibration and data inefficiency. Alas, scaling Bayesian inference to large weight spaces often requires restrictive approximations. In this work, we show that it suffices to perform inference over a small subset of model weights in order to obtain accurate predictive posteriors. The other weights are kept as point estimates. This subnetwork inference framework enables us to use expressive, otherwise intractable, posterior approximations over such subsets. In particular, we implement subnetwork linearized Laplace: We first obtain a MAP estimate of all weights and then infer a full-covariance Gaussian posterior over a subnetwork. We propose a subnetwork selection strategy that aims to maximally preserve the model's predictive uncertainty. Empirically, our approach is effective compared to ensembles and less expressive posterior approximations over full networks.
Embedding entities and relations into a continuous multi-dimensional vector space have become the dominant method for knowledge graph embedding in representation learning. However, most existing models ignore to represent hierarchical knowledge, such as the similarities and dissimilarities of entities in one domain. We proposed to learn a Domain Representations over existing knowledge graph embedding models, such that entities that have similar attributes are organized into the same domain. Such hierarchical knowledge of domains can give further evidence in link prediction. Experimental results show that domain embeddings give a significant improvement over the most recent state-of-art baseline knowledge graph embedding models.
Graph neural networks (GNNs) are a popular class of machine learning models whose major advantage is their ability to incorporate a sparse and discrete dependency structure between data points. Unfortunately, GNNs can only be used when such a graph-structure is available. In practice, however, real-world graphs are often noisy and incomplete or might not be available at all. With this work, we propose to jointly learn the graph structure and the parameters of graph convolutional networks (GCNs) by approximately solving a bilevel program that learns a discrete probability distribution on the edges of the graph. This allows one to apply GCNs not only in scenarios where the given graph is incomplete or corrupted but also in those where a graph is not available. We conduct a series of experiments that analyze the behavior of the proposed method and demonstrate that it outperforms related methods by a significant margin.
Deep neural network architectures have traditionally been designed and explored with human expertise in a long-lasting trial-and-error process. This process requires huge amount of time, expertise, and resources. To address this tedious problem, we propose a novel algorithm to optimally find hyperparameters of a deep network architecture automatically. We specifically focus on designing neural architectures for medical image segmentation task. Our proposed method is based on a policy gradient reinforcement learning for which the reward function is assigned a segmentation evaluation utility (i.e., dice index). We show the efficacy of the proposed method with its low computational cost in comparison with the state-of-the-art medical image segmentation networks. We also present a new architecture design, a densely connected encoder-decoder CNN, as a strong baseline architecture to apply the proposed hyperparameter search algorithm. We apply the proposed algorithm to each layer of the baseline architectures. As an application, we train the proposed system on cine cardiac MR images from Automated Cardiac Diagnosis Challenge (ACDC) MICCAI 2017. Starting from a baseline segmentation architecture, the resulting network architecture obtains the state-of-the-art results in accuracy without performing any trial-and-error based architecture design approaches or close supervision of the hyperparameters changes.
Deep neural networks (DNNs) have been found to be vulnerable to adversarial examples resulting from adding small-magnitude perturbations to inputs. Such adversarial examples can mislead DNNs to produce adversary-selected results. Different attack strategies have been proposed to generate adversarial examples, but how to produce them with high perceptual quality and more efficiently requires more research efforts. In this paper, we propose AdvGAN to generate adversarial examples with generative adversarial networks (GANs), which can learn and approximate the distribution of original instances. For AdvGAN, once the generator is trained, it can generate adversarial perturbations efficiently for any instance, so as to potentially accelerate adversarial training as defenses. We apply AdvGAN in both semi-whitebox and black-box attack settings. In semi-whitebox attacks, there is no need to access the original target model after the generator is trained, in contrast to traditional white-box attacks. In black-box attacks, we dynamically train a distilled model for the black-box model and optimize the generator accordingly. Adversarial examples generated by AdvGAN on different target models have high attack success rate under state-of-the-art defenses compared to other attacks. Our attack has placed the first with 92.76% accuracy on a public MNIST black-box attack challenge.
The dominant sequence transduction models are based on complex recurrent or convolutional neural networks in an encoder-decoder configuration. The best performing models also connect the encoder and decoder through an attention mechanism. We propose a new simple network architecture, the Transformer, based solely on attention mechanisms, dispensing with recurrence and convolutions entirely. Experiments on two machine translation tasks show these models to be superior in quality while being more parallelizable and requiring significantly less time to train. Our model achieves 28.4 BLEU on the WMT 2014 English-to-German translation task, improving over the existing best results, including ensembles by over 2 BLEU. On the WMT 2014 English-to-French translation task, our model establishes a new single-model state-of-the-art BLEU score of 41.8 after training for 3.5 days on eight GPUs, a small fraction of the training costs of the best models from the literature. We show that the Transformer generalizes well to other tasks by applying it successfully to English constituency parsing both with large and limited training data.