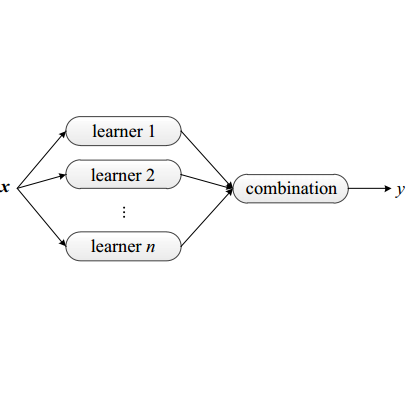
Time series forecasting plays a crucial role in diverse fields, necessitating the development of robust models that can effectively handle complex temporal patterns. In this article, we present a novel feature selection method embedded in Long Short-Term Memory networks, leveraging a multi-objective evolutionary algorithm. Our approach optimizes the weights and biases of the LSTM in a partitioned manner, with each objective function of the evolutionary algorithm targeting the root mean square error in a specific data partition. The set of non-dominated forecast models identified by the algorithm is then utilized to construct a meta-model through stacking-based ensemble learning. Furthermore, our proposed method provides an avenue for attribute importance determination, as the frequency of selection for each attribute in the set of non-dominated forecasting models reflects their significance. This attribute importance insight adds an interpretable dimension to the forecasting process. Experimental evaluations on air quality time series data from Italy and southeast Spain demonstrate that our method substantially improves the generalization ability of conventional LSTMs, effectively reducing overfitting. Comparative analyses against state-of-the-art CancelOut and EAR-FS methods highlight the superior performance of our approach.
相關內容

We introduce a novel Dual Input Stream Transformer (DIST) for the challenging problem of assigning fixation points from eye-tracking data collected during passage reading to the line of text that the reader was actually focused on. This post-processing step is crucial for analysis of the reading data due to the presence of noise in the form of vertical drift. We evaluate DIST against eleven classical approaches on a comprehensive suite of nine diverse datasets. We demonstrate that combining multiple instances of the DIST model in an ensemble achieves high accuracy across all datasets. Further combining the DIST ensemble with the best classical approach yields an average accuracy of 98.17 %. Our approach presents a significant step towards addressing the bottleneck of manual line assignment in reading research. Through extensive analysis and ablation studies, we identify key factors that contribute to DIST's success, including the incorporation of line overlap features and the use of a second input stream. Via rigorous evaluation, we demonstrate that DIST is robust to various experimental setups, making it a safe first choice for practitioners in the field.
We give a fully polynomial-time randomized approximation scheme (FPRAS) for two terminal reliability in directed acyclic graphs (DAGs). In contrast, we also show the complementing problem of approximating two terminal unreliability in DAGs is #BIS-hard.
The present article is concerned scattered data approximation for higher dimensional data sets which exhibit an anisotropic behavior in the different dimensions. Tailoring sparse polynomial interpolation to this specific situation, we derive very efficient degenerate kernel approximations which we then use in a dimension weighted fast multipole method. This dimension weighted fast multipole method enables to deal with many more dimensions than the standard black-box fast multipole method based on interpolation. A thorough analysis of the method is provided including rigorous error estimates. The accuracy and the cost of the approach are validated by extensive numerical results. As a relevant application, we apply the approach to a shape uncertainty quantification problem.
This paper is concerned with the problem of sampling and interpolation involving derivatives in shift-invariant spaces and the error analysis of the derivative sampling expansions for fundamentally large classes of functions. A new type of polynomials based on derivative samples is introduced, which is different from the Euler-Frobenius polynomials for the multiplicity $r>1$. A complete characterization of uniform sampling with derivatives is given using Laurent operators. The rate of approximation of a signal (not necessarily continuous) by the derivative sampling expansions in shift-invariant spaces generated by compactly supported functions is established in terms of $L^p$- average modulus of smoothness. Finally, several typical examples illustrating the various problems are discussed in detail.
Mesh-based Graph Neural Networks (GNNs) have recently shown capabilities to simulate complex multiphysics problems with accelerated performance times. However, mesh-based GNNs require a large number of message-passing (MP) steps and suffer from over-smoothing for problems involving very fine mesh. In this work, we develop a multiscale mesh-based GNN framework mimicking a conventional iterative multigrid solver, coupled with adaptive mesh refinement (AMR), to mitigate challenges with conventional mesh-based GNNs. We use the framework to accelerate phase field (PF) fracture problems involving coupled partial differential equations with a near-singular operator due to near-zero modulus inside the crack. We define the initial graph representation using all mesh resolution levels. We perform a series of downsampling steps using Transformer MP GNNs to reach the coarsest graph followed by upsampling steps to reach the original graph. We use skip connectors from the generated embedding during coarsening to prevent over-smoothing. We use Transfer Learning (TL) to significantly reduce the size of training datasets needed to simulate different crack configurations and loading conditions. The trained framework showed accelerated simulation times, while maintaining high accuracy for all cases compared to physics-based PF fracture model. Finally, this work provides a new approach to accelerate a variety of mesh-based engineering multiphysics problems
Dynamical low-rank approximation has become a valuable tool to perform an on-the-fly model order reduction for prohibitively large matrix differential equations. A core ingredient is the construction of integrators that are robust to the presence of small singular values and the resulting large time derivatives of the orthogonal factors in the low-rank matrix representation. Recently, the robust basis-update & Galerkin (BUG) class of integrators has been introduced. These methods require no steps that evolve the solution backward in time, often have favourable structure-preserving properties, and allow for parallel time-updates of the low-rank factors. The BUG framework is flexible enough to allow for adaptations to these and further requirements. However, the BUG methods presented so far have only first-order robust error bounds. This work proposes a second-order BUG integrator for dynamical low-rank approximation based on the midpoint rule. The integrator first performs a half-step with a first-order BUG integrator, followed by a Galerkin update with a suitably augmented basis. We prove a robust second-order error bound which in addition shows an improved dependence on the normal component of the vector field. These rigorous results are illustrated and complemented by a number of numerical experiments.
We study the problem of training diffusion models to sample from a distribution with a given unnormalized density or energy function. We benchmark several diffusion-structured inference methods, including simulation-based variational approaches and off-policy methods (continuous generative flow networks). Our results shed light on the relative advantages of existing algorithms while bringing into question some claims from past work. We also propose a novel exploration strategy for off-policy methods, based on local search in the target space with the use of a replay buffer, and show that it improves the quality of samples on a variety of target distributions. Our code for the sampling methods and benchmarks studied is made public at //github.com/GFNOrg/gfn-diffusion as a base for future work on diffusion models for amortized inference.
We propose new methods to obtain simultaneous false discovery proportion bounds for knockoff-based approaches. We first investigate an approach based on Janson and Su's $k$-familywise error rate control method and interpolation. We then generalize it by considering a collection of $k$ values, and show that the bound of Katsevich and Ramdas is a special case of this method and can be uniformly improved. Next, we further generalize the method by using closed testing with a multi-weighted-sum local test statistic. This allows us to obtain a further uniform improvement and other generalizations over previous methods. We also develop an efficient shortcut for its implementation. We compare the performance of our proposed methods in simulations and apply them to a data set from the UK Biobank.
We study the modeling and forecasting of high-dimensional functional time series (HDFTS), which can be cross-sectionally correlated and temporally dependent. We introduce a decomposition of the HDFTS into two distinct components: a deterministic component and a residual component that varies over time. The decomposition is derived through the estimation of two-way functional analysis of variance. A functional time series forecasting method, based on functional principal component analysis, is implemented to produce forecasts for the residual component. By combining the forecasts of the residual component with the deterministic component, we obtain forecast curves for multiple populations. We apply the model to age- and sex-specific mortality rates in the United States, France, and Japan, in which there are 51 states, 95 departments, and 47 prefectures, respectively. The proposed method is capable of delivering more accurate point and interval forecasts in forecasting multi-population mortality than several benchmark methods considered.
Time Series Classification (TSC) is an important and challenging problem in data mining. With the increase of time series data availability, hundreds of TSC algorithms have been proposed. Among these methods, only a few have considered Deep Neural Networks (DNNs) to perform this task. This is surprising as deep learning has seen very successful applications in the last years. DNNs have indeed revolutionized the field of computer vision especially with the advent of novel deeper architectures such as Residual and Convolutional Neural Networks. Apart from images, sequential data such as text and audio can also be processed with DNNs to reach state-of-the-art performance for document classification and speech recognition. In this article, we study the current state-of-the-art performance of deep learning algorithms for TSC by presenting an empirical study of the most recent DNN architectures for TSC. We give an overview of the most successful deep learning applications in various time series domains under a unified taxonomy of DNNs for TSC. We also provide an open source deep learning framework to the TSC community where we implemented each of the compared approaches and evaluated them on a univariate TSC benchmark (the UCR/UEA archive) and 12 multivariate time series datasets. By training 8,730 deep learning models on 97 time series datasets, we propose the most exhaustive study of DNNs for TSC to date.