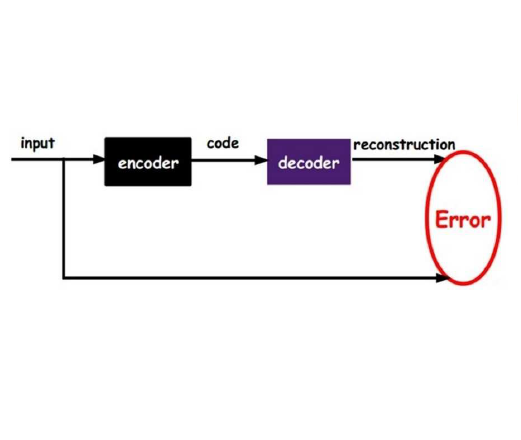
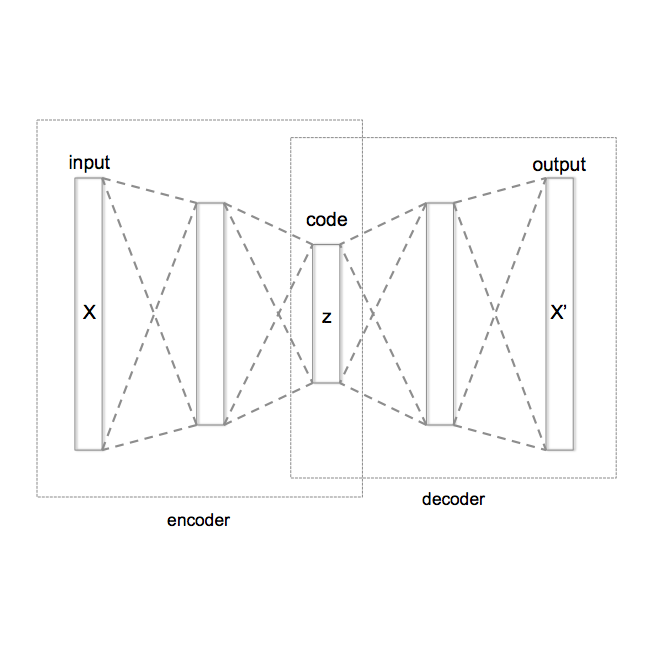
The crystal diffusion variational autoencoder (CDVAE) is a machine learning model that leverages score matching to generate realistic crystal structures that preserve crystal symmetry. In this study, we leverage novel diffusion probabilistic (DP) models to denoise atomic coordinates rather than adopting the standard score matching approach in CDVAE. Our proposed DP-CDVAE model can reconstruct and generate crystal structures whose qualities are statistically comparable to those of the original CDVAE. Furthermore, notably, when comparing the carbon structures generated by the DP-CDVAE model with relaxed structures obtained from density functional theory calculations, we find that the DP-CDVAE generated structures are remarkably closer to their respective ground states. The energy differences between these structures and the true ground states are, on average, 68.1 meV/atom lower than those generated by the original CDVAE. This significant improvement in the energy accuracy highlights the effectiveness of the DP-CDVAE model in generating crystal structures that better represent their ground-state configurations.
相關內容
Crystalline phase structure is essential for understanding the performance and properties of a material. Therefore, this study identified and quantified the crystalline phase structure of a sample based on the diffraction pattern observed when the crystalline sample was irradiated with electromagnetic waves such as X-rays. Conventional analysis necessitates experienced and knowledgeable researchers to shorten the list from many candidate crystalline phase structures. However, the Conventional diffraction pattern analysis is highly analyst-dependent and not objective. Additionally, there is no established method for discussing the confidence intervals of the analysis results. Thus, this study aimed to establish a method for automatically inferring crystalline phase structures from diffraction patterns using Bayesian inference. Our method successfully identified true crystalline phase structures with a high probability from 50 candidate crystalline phase structures. Further, the mixing ratios of selected crystalline phase structures were estimated with a high degree of accuracy. This study provided reasonable results for well-crystallized samples that clearly identified the crystalline phase structures.
The problem of sequential anomaly detection and identification is considered in the presence of a sampling constraint. Specifically, multiple data streams are generated by distinct sources and the goal is to quickly identify those that exhibit ``anomalous'' behavior, when it is not possible to sample every source at each time instant. Thus, in addition to a stopping rule, which determines when to stop sampling, and a decision rule, which indicates which sources to identify as anomalous upon stopping, one needs to specify a sampling rule that determines which sources to sample at each time instant. The focus of this work is on ordering sampling rules, which sample the data sources, among those currently estimated as anomalous (resp. non-anomalous), for which the corresponding local test statistics have the smallest (resp. largest) values. It is shown that with an appropriate design, which is specified explicitly, an ordering sampling rule leads to the optimal expected time for stopping, among all policies that satisfy the same sampling and error constraints, to a first-order asymptotic approximation as the false positive and false negative error rates under control both go to zero. This is the first asymptotic optimality result for ordering sampling rules when multiple sources can be sampled per time instant. Moreover, this is established under a general setup where the number of anomalies is not required to be a priori known. A novel proof technique is introduced, which unifies different versions of the problem regarding the homogeneity of the sources and prior information on the number of anomalies.
A problem related to the development of algorithms designed to find the structure of artificial neural network used for behavioural (black-box) modelling of selected dynamic processes has been addressed in this paper. The research has included four original proposals of algorithms dedicated to neural network architecture search. Algorithms have been based on well-known optimisation techniques such as evolutionary algorithms and gradient descent methods. In the presented research an artificial neural network of recurrent type has been used, whose architecture has been selected in an optimised way based on the above-mentioned algorithms. The optimality has been understood as achieving a trade-off between the size of the neural network and its accuracy in capturing the response of the mathematical model under which it has been learnt. During the optimisation, original specialised evolutionary operators have been proposed. The research involved an extended validation study based on data generated from a mathematical model of the fast processes occurring in a pressurised water nuclear reactor.
Multi-level modeling is an important approach for analyzing complex survey data using multi-stage sampling. However, estimation of multi-level models can be challenging when we combine several datasets with distinct hierarchies with sampling weights. This paper presents a method for combining multiple datasets with different hierarchical structures due to distinct informative sampling designs for the same survey. To develop an approach with complete generality, we propose to define a pseudo-cluster, a cluster containing only a singleton observation, to unify the data structure and thereby enable estimation of multi-level models incorporating sampling weights across the combined sample. We justify incorporating sampling weights at each level of the hierarchical model and in doing-so define a pseudo-likelihood estimation procedure. Simulation studies are used to illustrate the effect of incorporating sampling designs in this challenging multi-level modeling scenario. We demonstrate in the simulation studies that considering a linear mixed model with sampling weights provides unbiased estimates of model parameters and enhances the estimation of the variance components of the random effects. The proposed method is illustrated through a novel application from the National Survey of Healthcare Organizations and Systems that sought to determine which organizational characteristics or traits, as measured in the surveys, have the strongest average relationship to the percentage of depression and anxiety diagnoses in physician practices in the US.
The numerical solution of continuum damage mechanics (CDM) problems suffers from convergence-related challenges during the material softening stage, and consequently existing iterative solvers are subject to a trade-off between computational expense and solution accuracy. In this work, we present a novel unified arc-length (UAL) method, and we derive the formulation of the analytical tangent matrix and governing system of equations for both local and non-local gradient damage problems. Unlike existing versions of arc-length solvers that monolithically scale the external force vector, the proposed method treats the latter as an independent variable and determines the position of the system on the equilibrium path based on all the nodal variations of the external force vector. This approach renders the proposed solver substantially more efficient and robust than existing solvers used in CDM problems. We demonstrate the considerable advantages of the proposed algorithm through several benchmark 1D problems with sharp snap-backs and 2D examples under various boundary conditions and loading scenarios. The proposed UAL approach exhibits a superior ability of overcoming critical increments along the equilibrium path. Moreover, the proposed UAL method is 1-2 orders of magnitude faster than force-controlled arc-length and monolithic Newton-Raphson solvers.
We investigate the combinatorics of max-pooling layers, which are functions that downsample input arrays by taking the maximum over shifted windows of input coordinates, and which are commonly used in convolutional neural networks. We obtain results on the number of linearity regions of these functions by equivalently counting the number of vertices of certain Minkowski sums of simplices. We characterize the faces of such polytopes and obtain generating functions and closed formulas for the number of vertices and facets in a 1D max-pooling layer depending on the size of the pooling windows and stride, and for the number of vertices in a special case of 2D max-pooling.
We propose a new class of models for variable clustering called Asymptotic Independent block (AI-block) models, which defines population-level clusters based on the independence of the maxima of a multivariate stationary mixing random process among clusters. This class of models is identifiable, meaning that there exists a maximal element with a partial order between partitions, allowing for statistical inference. We also present an algorithm for recovering the clusters of variables without specifying the number of clusters \emph{a priori}. Our work provides some theoretical insights into the consistency of our algorithm, demonstrating that under certain conditions it can effectively identify clusters in the data with a computational complexity that is polynomial in the dimension. This implies that groups can be learned nonparametrically in which block maxima of a dependent process are only sub-asymptotic. To further illustrate the significance of our work, we applied our method to neuroscience and environmental real-datasets. These applications highlight the potential and versatility of the proposed approach.
Most existing methods for unsupervised industrial anomaly detection train a separate model for each object category. This kind of approach can easily capture the category-specific feature distributions, but results in high storage cost and low training efficiency. In this paper, we propose a unified mixed-attention auto encoder (MAAE) to implement multi-class anomaly detection with a single model. To alleviate the performance degradation due to the diverse distribution patterns of different categories, we employ spatial attentions and channel attentions to effectively capture the global category information and model the feature distributions of multiple classes. Furthermore, to simulate the realistic noises on features and preserve the surface semantics of objects from different categories which are essential for detecting the subtle anomalies, we propose an adaptive noise generator and a multi-scale fusion module for the pre-trained features. MAAE delivers remarkable performances on the benchmark dataset compared with the state-of-the-art methods.
A robust nonconforming mixed finite element method is developed for a strain gradient elasticity (SGE) model. In two and three dimensional cases, a lower order $C^0$-continuous $H^2$-nonconforming finite element is constructed for the displacement field through enriching the quadratic Lagrange element with bubble functions. This together with the linear Lagrange element is exploited to discretize a mixed formulation of the SGE model. The robust discrete inf-sup condition is established. The sharp and uniform error estimates with respect to both the small size parameter and the Lam\'{e} coefficient are achieved, which is also verified by numerical results. In addition, the uniform regularity of the SGE model is derived under two reasonable assumptions.
We propose an approach to compute inner and outer-approximations of the sets of values satisfying constraints expressed as arbitrarily quantified formulas. Such formulas arise for instance when specifying important problems in control such as robustness, motion planning or controllers comparison. We propose an interval-based method which allows for tractable but tight approximations. We demonstrate its applicability through a series of examples and benchmarks using a prototype implementation.