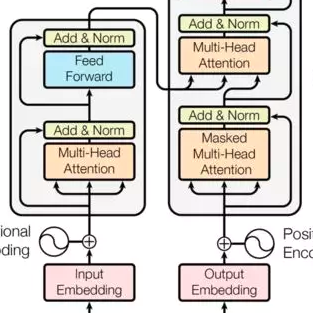
Since the success of GPT, large language models (LLMs) have been revolutionizing machine learning and have initiated the so-called LLM prompting paradigm. In the era of LLMs, people train a single general-purpose LLM and provide the LLM with different prompts to perform different tasks. However, such empirical success largely lacks theoretical understanding. Here, we present the first theoretical study on the LLM prompting paradigm to the best of our knowledge. In this work, we show that prompting is in fact Turing-complete: there exists a finite-size Transformer such that for any computable function, there exists a corresponding prompt following which the Transformer computes the function. Furthermore, we show that even though we use only a single finite-size Transformer, it can still achieve nearly the same complexity bounds as that of the class of all unbounded-size Transformers. Overall, our result reveals that prompting can enable a single finite-size Transformer to be efficiently universal, which establishes a theoretical underpinning for prompt engineering in practice.
相關內容
Random Forests have become a widely used tool in machine learning since their introduction in 2001, known for their strong performance in classification and regression tasks. One key feature of Random Forests is the Random Forest Permutation Importance Measure (RFPIM), an internal, non-parametric measure of variable importance. While widely used, theoretical work on RFPIM is sparse, and most research has focused on empirical findings. However, recent progress has been made, such as establishing consistency of the RFPIM, although a mathematical analysis of its asymptotic distribution is still missing. In this paper, we provide a formal proof of a Central Limit Theorem for RFPIM using U-Statistics theory. Our approach deviates from the conventional Random Forest model by assuming a random number of trees and imposing conditions on the regression functions and error terms, which must be bounded and additive, respectively. Our result aims at improving the theoretical understanding of RFPIM rather than conducting comprehensive hypothesis testing. However, our contributions provide a solid foundation and demonstrate the potential for future work to extend to practical applications which we also highlight with a small simulation study.
When dealing with a large number of points was required, the traditional uniform sampling approach for approximating integrals using the Monte Carlo method becomes inefficient. In this work, we leverage the good lattice point sets from number-theoretic methods for sampling purposes and develop a deep learning framework that integrates the good lattice point sets with Physics-Informed Neural Networks. This framework is designed to address low-regularity and high-dimensional problems. Furthermore, rigorous mathematical proofs are provided for our algorithm, demonstrating its validity. Lastly, in the experimental section, we employ numerical experiments involving the Poisson equation with low regularity, the two-dimensional inverse Helmholtz equation, and high-dimensional linear and nonlinear problems to illustrate the effectiveness of our algorithm from a numerical perspective.
Program-of-Thought (PoT), which aims to use programming language instead of natural language as an intermediate step in reasoning, is an important way for LLMs to solve mathematical problems. Since different programming languages excel in different areas, it is natural to use the most suitable language for solving specific problems. However, current PoT research only focuses on single language PoT, ignoring the differences between different programming languages. Therefore, this paper proposes an multilingual program reasoning method, MultiLingPoT. This method allows the model to answer questions using multiple programming languages by fine-tuning on multilingual data. Additionally, prior and posterior hybrid methods are used to help the model select the most suitable language for each problem. Our experimental results show that the training of MultiLingPoT improves each program's mathematical reasoning by about 2.5\%. Moreover, with proper mixing, the performance of MultiLingPoT can be further improved, achieving a 6\% increase compared to the single-language PoT with the data augmentation.Resources of this paper can be found at //github.com/Nianqi-Li/MultiLingPoT.
The Mapper algorithm is an essential tool for visualizing complex, high dimensional data in topology data analysis (TDA) and has been widely used in biomedical research. It outputs a combinatorial graph whose structure implies the shape of the data. However,the need for manual parameter tuning and fixed intervals, along with fixed overlapping ratios may impede the performance of the standard Mapper algorithm. Variants of the standard Mapper algorithms have been developed to address these limitations, yet most of them still require manual tuning of parameters. Additionally, many of these variants, including the standard version found in the literature, were built within a deterministic framework and overlooked the uncertainty inherent in the data. To relax these limitations, in this work, we introduce a novel framework that implicitly represents intervals through a hidden assignment matrix, enabling automatic parameter optimization via stochastic gradient descent. In this work, we develop a soft Mapper framework based on a Gaussian mixture model(GMM) for flexible and implicit interval construction. We further illustrate the robustness of the soft Mapper algorithm by introducing the Mapper graph mode as a point estimation for the output graph. Moreover, a stochastic gradient descent algorithm with a specific topological loss function is proposed for optimizing parameters in the model. Both simulation and application studies demonstrate its effectiveness in capturing the underlying topological structures. In addition, the application to an RNA expression dataset obtained from the Mount Sinai/JJ Peters VA Medical Center Brain Bank (MSBB) successfully identifies a distinct subgroup of Alzheimer's Disease.
Most of the scientific literature on causal modeling considers the structural framework of Pearl and the potential-outcome framework of Rubin to be formally equivalent, and therefore interchangeably uses do-interventions and the potential-outcome subscript notation to write counterfactual outcomes. In this paper, we agnostically superimpose the two causal models to specify under which mathematical conditions structural counterfactual outcomes and potential outcomes need to, do not need to, can, or cannot be equal (almost surely or law). Our comparison reminds that a structural causal model and a Rubin causal model compatible with the same observations do not have to coincide, and highlights real-world problems where they even cannot correspond. Then, we examine common claims and practices from the causal-inference literature in the light of these results. In doing so, we aim at clarifying the relationship between the two causal frameworks, and the interpretation of their respective counterfactuals.
Subclasses of TFNP (total functional NP) are usually defined by specifying a complete problem, which is necessarily in TFNP, and including all problems many-one reducible to it. We study two notions of how a TFNP problem can be reducible to an object, such as a complexity class, outside TFNP. This gives rise to subclasses of TFNP which capture some properties of that outside object. We show that well-known subclasses can arise in this way, for example PPA from reducibility to parity P and PLS from reducibility to P^NP. We study subclasses arising from PSPACE and the polynomial hierarchy, and show that they are characterized by the propositional proof systems Frege and constant-depth Frege, extending the known pairings between natural TFNP subclasses and proof systems. We study approximate counting from this point of view, and look for a subclass of TFNP that gives a natural home to combinatorial principles such as Ramsey which can be proved using approximate counting. We relate this to the recently-studied Long choice and Short choice problems.
Federated Learning (FL) is a machine learning paradigm in which many clients cooperatively train a single centralized model while keeping their data private and decentralized. FL is commonly used in edge computing, which involves placing computer workloads (both hardware and software) as close as possible to the edge, where the data is being created and where actions are occurring, enabling faster response times, greater data privacy, and reduced data transfer costs. However, due to the heterogeneous data distributions/contents of clients, it is non-trivial to accurately evaluate the contributions of local models in global centralized model aggregation. This is an example of a major challenge in FL, commonly known as data imbalance or class imbalance. In general, testing and assessing FL algorithms can be a very difficult and complex task due to the distributed nature of the systems. In this work, a framework is proposed and implemented to assess FL algorithms in a more easy and scalable way. This framework is evaluated over a distributed edge-like environment managed by a container orchestration platform (i.e. Kubernetes).
Large Language Models (LLMs) have demonstrated great potential in various language processing tasks, and recent studies have explored their application in compiler optimizations. However, all these studies focus on the conventional open-source LLMs, such as Llama2, which lack enhanced reasoning mechanisms. In this study, we investigate the errors produced by the fine-tuned 7B-parameter Llama2 model as it attempts to learn and apply a simple peephole optimization for the AArch64 assembly code. We provide an analysis of the errors produced by the LLM and compare it with state-of-the-art OpenAI models which implement advanced reasoning logic, including GPT-4o and GPT-o1 (preview). We demonstrate that OpenAI GPT-o1, despite not being fine-tuned, outperforms the fine-tuned Llama2 and GPT-4o. Our findings indicate that this advantage is largely due to the chain-of-thought reasoning implemented in GPT-o1. We hope our work will inspire further research on using LLMs with enhanced reasoning mechanisms and chain-of-thought for code generation and optimization.
Recently pre-trained language representation models such as BERT have shown great success when fine-tuned on downstream tasks including information retrieval (IR). However, pre-training objectives tailored for ad-hoc retrieval have not been well explored. In this paper, we propose Pre-training with Representative wOrds Prediction (PROP) for ad-hoc retrieval. PROP is inspired by the classical statistical language model for IR, specifically the query likelihood model, which assumes that the query is generated as the piece of text representative of the "ideal" document. Based on this idea, we construct the representative words prediction (ROP) task for pre-training. Given an input document, we sample a pair of word sets according to the document language model, where the set with higher likelihood is deemed as more representative of the document. We then pre-train the Transformer model to predict the pairwise preference between the two word sets, jointly with the Masked Language Model (MLM) objective. By further fine-tuning on a variety of representative downstream ad-hoc retrieval tasks, PROP achieves significant improvements over baselines without pre-training or with other pre-training methods. We also show that PROP can achieve exciting performance under both the zero- and low-resource IR settings. The code and pre-trained models are available at //github.com/Albert-Ma/PROP.
Recently, the emergence of pre-trained models (PTMs) has brought natural language processing (NLP) to a new era. In this survey, we provide a comprehensive review of PTMs for NLP. We first briefly introduce language representation learning and its research progress. Then we systematically categorize existing PTMs based on a taxonomy with four perspectives. Next, we describe how to adapt the knowledge of PTMs to the downstream tasks. Finally, we outline some potential directions of PTMs for future research. This survey is purposed to be a hands-on guide for understanding, using, and developing PTMs for various NLP tasks.