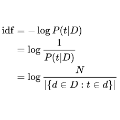亚洲男人的天堂2018av,欧美草比,久久久久久免费视频精选,国色天香在线看免费,久久久久亚洲av成人片仓井空

The presence of faulty or underactuated manipulators can disrupt the end-effector formation keeping of a team of manipulators. Based on two-link planar manipulators, we investigate this end-effector formation keeping problem for mixed fully- and under-actuated manipulators with flexible joints. In this case, the underactuated manipulators can comprise of active-passive (AP) manipulators, passive-active (PA) manipulators, or a combination thereof. We propose distributed control laws for the different types of manipulators to achieve and maintain the desired formation shape of the end-effectors. It is achieved by assigning virtual springs to the end-effectors for the fully-actuated ones and to the virtual end-effectors for the under-actuated ones. We study further the set of all desired and reachable shapes for the networked manipulators' end-effectors. Finally, we validate our analysis via numerical simulations.

We propose a classification of all one-dimensional discrete statistical models with maximum likelihood degree one based on their rational parametrization. We show how all such models can be constructed from members of a smaller class of 'fundamental models' using a finite number of simple operations. We introduce 'chipsplitting games', a class of combinatorial games on a grid which we use to represent fundamental models. This combinatorial perspective enables us to show that there are only finitely many fundamental models in the probability simplex $\Delta_n$ for $n\leq 4$.

A discretization method with non-matching grids is proposed for the coupled Stokes-Darcy problem that uses a mortar variable at the interface to couple the marker and cell (MAC) method in the Stokes domain with the Raviart-Thomas mixed finite element pair in the Darcy domain. Due to this choice, the method conserves linear momentum and mass locally in the Stokes domain and exhibits local mass conservation in the Darcy domain. The MAC scheme is reformulated as a mixed finite element method on a staggered grid, which allows for the proposed scheme to be analyzed as a mortar mixed finite element method. We show that the discrete system is well-posed and derive a priori error estimates that indicate first order convergence in all variables. The system can be reduced to an interface problem concerning only the mortar variables, leading to a non-overlapping domain decomposition method. Numerical examples are presented to illustrate the theoretical results and the applicability of the method.

We propose and discuss Bayesian machine learning methods for mixed data sampling (MIDAS) regressions. This involves handling frequency mismatches with restricted and unrestricted MIDAS variants and specifying functional relationships between many predictors and the dependent variable. We use Gaussian processes (GP) and Bayesian additive regression trees (BART) as flexible extensions to linear penalized estimation. In a nowcasting and forecasting exercise we focus on quarterly US output growth and inflation in the GDP deflator. The new models leverage macroeconomic Big Data in a computationally efficient way and offer gains in predictive accuracy along several dimensions.

Data in the form of rankings, ratings, pair comparisons or clicks are frequently collected in diverse fields, from marketing to politics, to understand assessors' individual preferences. Combining such preference data with features associated with the assessors can lead to a better understanding of the assessors' behaviors and choices. The Mallows model is a popular model for rankings, as it flexibly adapts to different types of preference data, and the previously proposed Bayesian Mallows Model (BMM) offers a computationally efficient framework for Bayesian inference, also allowing capturing the users' heterogeneity via a finite mixture. We develop a Bayesian Mallows-based finite mixture model that performs clustering while also accounting for assessor-related features, called the Bayesian Mallows model with covariates (BMMx). BMMx is based on a similarity function that a priori favours the aggregation of assessors into a cluster when their covariates are similar, using the Product Partition models (PPMx) proposal. We present two approaches to measure the covariate similarity: one based on a novel deterministic function measuring the covariates' goodness-of-fit to the cluster, and one based on an augmented model as in PPMx. We investigate the performance of BMMx in both simulation experiments and real-data examples, showing the method's potential for advancing the understanding of assessor preferences and behaviors in different applications.

We prove tight probabilistic bounds for the shortest vectors in module lattices over number fields using the results of arXiv:2308.15275. Moreover, establishing asymptotic formulae for counts of fixed rank matrices with algebraic integer entries and bounded Euclidean length, we prove an approximate Rogers integral formula for discrete sets of module lattices obtained from lifts of algebraic codes. This in turn implies that the moment estimates of arXiv:2308.15275 as well as the aforementioned bounds on the shortest vector also carry through for large enough discrete sets of module lattices.

Under a generalised estimating equation analysis approach, approximate design theory is used to determine Bayesian D-optimal designs. For two examples, considering simple exchangeable and exponential decay correlation structures, we compare the efficiency of identified optimal designs to balanced stepped-wedge designs and corresponding stepped-wedge designs determined by optimising using a normal approximation approach. The dependence of the Bayesian D-optimal designs on the assumed correlation structure is explored; for the considered settings, smaller decay in the correlation between outcomes across time periods, along with larger values of the intra-cluster correlation, leads to designs closer to a balanced design being optimal. Unlike for normal data, it is shown that the optimal design need not be centro-symmetric in the binary outcome case. The efficiency of the Bayesian D-optimal design relative to a balanced design can be large, but situations are demonstrated in which the advantages are small. Similarly, the optimal design from a normal approximation approach is often not much less efficient than the Bayesian D-optimal design. Bayesian D-optimal designs can be readily identified for stepped-wedge cluster randomised trials with binary outcome data. In certain circumstances, principally ones with strong time period effects, they will indicate that a design unlikely to have been identified by previous methods may be substantially more efficient. However, they require a larger number of assumptions than existing optimal designs, and in many situations existing theory under a normal approximation will provide an easier means of identifying an efficient design for binary outcome data.

Linear mixed models are commonly used in analyzing stepped-wedge cluster randomized trials (SW-CRTs). A key consideration for analyzing a SW-CRT is accounting for the potentially complex correlation structure, which can be achieved by specifying a random effects structure. Common random effects structures for a SW-CRT include random intercept, random cluster-by-period, and discrete-time decay. Recently, more complex structures, such as the random intervention structure, have been proposed. In practice, specifying appropriate random effects can be challenging. Robust variance estimators (RVE) may be applied to linear mixed models to provide consistent estimators of standard errors of fixed effect parameters in the presence of random-effects misspecification. However, there has been no empirical investigation of RVE for SW-CRT. In this paper, we first review five RVEs (both standard and small-sample bias-corrected RVEs) that are available for linear mixed models. We then describe a comprehensive simulation study to examine the performance of these RVEs for SW-CRTs with a continuous outcome under different data generators. For each data generator, we investigate whether the use of a RVE with either the random intercept model or the random cluster-by-period model is sufficient to provide valid statistical inference for fixed effect parameters, when these working models are subject to misspecification. Our results indicate that the random intercept and random cluster-by-period models with RVEs performed similarly. The CR3 RVE estimator, coupled with the number of clusters minus two degrees of freedom correction, consistently gave the best coverage results, but could be slightly anti-conservative when the number of clusters was below 16. We summarize the implications of our results for linear mixed model analysis of SW-CRTs in practice.

Expander graphs, due to their good mixing properties, are useful in many algorithms and combinatorial constructions. One can produce an expander graph with high probability by taking a random graph. For example, for the case of bipartite graphs of degree $d$ and $n$ vertices in each part we may take independently $d$ permutations of an $n$-element set and use them for edges. This construction is much simpler than all known explicit constructions of expanders and gives graphs with good mixing properties (small second largest eigenvalue) with high probability. However, from the practical viewpoint, it uses too many random bits, so it is difficult to generate and store these bits for reasonably large graphs. The natural idea is to replace the group of all permutations by its small subgroup. Let $n$ be $q^k-1$ for some $k$ and some prime $q$. Then we may interpret vertices as non-zero $k$-dimensional vector over the field $\mathbb{F}_q$, and take random \emph{linear} permutations, i.e., random elements of $GL_k(\mathbb{F}_q)$. In this way the number of random bits used will be polynomial in $k$ (i.e., the logarithm of the graph size, instead of the graph size itself) and the degree. In this paper we provide some experimental data that show that indeed this replacement does not change much the mixing properties (the second eigenvalue) of the random graph that we obtain. These data are provided for several types of graphs (undirected regular and biregular bipartite graphs). We also prove some upper bounds for the second eigenvalue (though it is quite weak compared with the experimental results). Finally, we discuss the possibility to decrease the number of random bits further by using Toeplitz matrices; our experiments show that this change makes the mixing properties of graphs only marginally worse, while the number of random bits decreases significantly.

Following initial work by JaJa and Ahlswede/Cai, and inspired by a recent renewed surge in interest in deterministic identification via noisy channels, we consider the problem in its generality for memoryless channels with finite output, but arbitrary input alphabets. Such a channel is essentially given by (the closure of) the subset of its output distributions in the probability simplex. Our main findings are that the maximum number of messages thus identifiable scales super-exponentially as $2^{R\,n\log n}$ with the block length $n$, and that the optimal rate $R$ is upper and lower bounded in terms of the covering (aka Minkowski, or Kolmogorov, or entropy) dimension $d$ of the output set: $\frac14 d \leq R \leq d$. Leading up to the general case, we treat the important special case of the so-called Bernoulli channel with input alphabet $[0;1]$ and binary output, which has $d=1$, to gain intuition. Along the way, we show a certain Hypothesis Testing Lemma (generalising an earlier insight of Ahlswede regarding the intersection of typical sets) that implies that for the construction of a deterministic identification code, it is sufficient to ensure pairwise reliable distinguishability of the output distributions. These results are then shown to generalise directly to classical-quantum channels with finite-dimensional output quantum system (but arbitrary input alphabet), and in particular to quantum channels on finite-dimensional quantum systems under the constraint that the identification code can only use tensor product inputs.