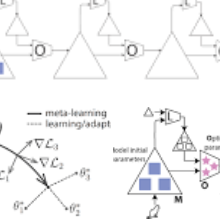
Data driven control of a continuum manipulator requires a lot of data for training but generating sufficient amount of real time data is not cost efficient. Random actuation of the manipulator can also be unsafe sometimes. Meta learning has been used successfully to adapt to a new environment. Hence, this paper tries to solve the above mentioned problem using meta learning. We consider two cases for that. First, this paper proposes a method to use simulation data for training the model using MAML(Model-Agnostic Meta-Learning). Then, it adapts to the real world using gradient steps. Secondly,if the simulation model is not available or difficult to formulate, then we propose a CGAN(Conditional Generative adversial network)-MAML based method for it. The model is trained using a small amount of real time data and augmented data for different loading conditions. Then, adaptation is done in the real environment. It has been found out from the experiments that the relative positioning error for both the cases are below 3%. The proposed models are experimentally verified on a real continuum manipulator.
相關內容
Overparameterized models that achieve zero training error are observed to generalize well on average, but degrade in performance when faced with data that is under-represented in the training sample. In this work, we study an overparameterized Gaussian mixture model imbued with a spurious feature, and sharply analyze the in-distribution and out-of-distribution test error of a cost-sensitive interpolating solution that incorporates "importance weights". Compared to recent work Wang et al. (2021), Behnia et al. (2022), our analysis is sharp with matching upper and lower bounds, and significantly weakens required assumptions on data dimensionality. Our error characterizations also apply to any choice of importance weights and unveil a novel tradeoff between worst-case robustness to distribution shift and average accuracy as a function of the importance weight magnitude.
For two real symmetric matrices, their eigenvalue configuration is the arrangement of their eigenvalues on the real line. We study the problem of determining a quantifier-free necessary and sufficient condition for two real symmetric matrices to realize a given eigenvalue configuration as a generalization of Descartes' rule of signs. We exploit the combinatorial properties of our definition for eigenvalue configuration to reduce a two-polynomial root counting problem into several single-polynomial root counting problems of symmetric polynomials. We then leverage the fundamental theorem of symmetric polynomials to derive a final quantifier-free necessary and sufficient condition for two real symmetric matrices to realize a given eigenvalue configuration.
For two real symmetric matrices, their eigenvalue configuration is the arrangement of their eigenvalues on the real line. In this paper, we provide quantifier-free necessary and sufficient conditions for two symmetric matrices to realize a given eigenvalue configuration. The basic idea is to generate a set of polynomials in the entries of the two matrices whose roots can be counted to uniquely determine the eigenvalue configuration. This result can be seen as ageneralization of Descartes' rule of signs to the case of two real univariate polynomials.
Hypothesis testing in high dimensional data is a notoriously difficult problem without direct access to competing models' likelihood functions. This paper argues that statistical divergences can be used to quantify the difference between the population distributions of observed data and competing models, justifying their use as the basis of a hypothesis test. We go on to point out how modern techniques for functional optimization let us estimate many divergences, without the need for population likelihood functions, using samples from two distributions alone. We use a physics-based example to show how the proposed two-sample test can be implemented in practice, and discuss the necessary steps required to mature the ideas presented into an experimental framework.
Bell sampling is a simple yet powerful measurement primitive that has recently attracted a lot of attention, and has proven to be a valuable tool in studying stabiliser states. Unfortunately, however, it is known that Bell sampling fails when used on qu\emph{d}its of dimension $d>2$. In this paper, we explore and quantify the limitations of Bell sampling on qudits, and propose new quantum algorithms to circumvent the use of Bell sampling in solving two important problems: learning stabiliser states and providing pseudorandomness lower bounds on qudits. More specifically, as our first result, we characterise the output distribution corresponding to Bell sampling on copies of a stabiliser state and show that the output can be uniformly random, and hence reveal no information. As our second result, for $d=p$ prime we devise a quantum algorithm to identify an unknown stabiliser state in $(\mathbb{C}^p)^{\otimes n}$ that uses $O(n)$ copies of the input state and runs in time $O(n^4)$. As our third result, we provide a quantum algorithm that efficiently distinguishes a Haar-random state from a state with non-negligible stabiliser fidelity. As a corollary, any Clifford circuit on qudits of dimension $d$ using $O(\log{n}/\log{d})$ auxiliary non-Clifford single-qudit gates cannot prepare computationally pseudorandom quantum states.
This short note is written for rapid communication of long context training and to share the idea of how to train it with low memory usage. In the note, we generalize the attention algorithm and neural network of Generative Pre-Trained Transformers and reinterpret it in Path integral formalism. First, the role of the transformer is understood as the time evolution of the token state and second, it is suggested that the all key-token states in the same time as the query-token can attend to the attention with the query token states. As a result of the repetitive time evolution, it is discussed that the token states in the past sequence meats the token states in the present sequence so that the attention between separated sequences becomes possible for maintaining infinite contextual information just by using low memory for limited size of sequence. For the experiment, the $12$ input token window size was taken and one GPU with $24$GB memory was used for the pre-training. It was confirmed that more than $150$ length context is preserved. The sampling result of the training, the code and the other details will be included in the revised version of this note later.
Many real-world processes have complex tail dependence structures that cannot be characterized using classical Gaussian processes. More flexible spatial extremes models exhibit appealing extremal dependence properties but are often exceedingly prohibitive to fit and simulate from in high dimensions. In this paper, we aim to push the boundaries on computation and modeling of high-dimensional spatial extremes via integrating a new spatial extremes model that has flexible and non-stationary dependence properties in the encoding-decoding structure of a variational autoencoder called the XVAE. The XVAE can emulate spatial observations and produce outputs that have the same statistical properties as the inputs, especially in the tail. Our approach also provides a novel way of making fast inference with complex extreme-value processes. Through extensive simulation studies, we show that our XVAE is substantially more time-efficient than traditional Bayesian inference while outperforming many spatial extremes models with a stationary dependence structure. Lastly, we analyze a high-resolution satellite-derived dataset of sea surface temperature in the Red Sea, which includes 30 years of daily measurements at 16703 grid cells. We demonstrate how to use XVAE to identify regions susceptible to marine heatwaves under climate change and examine the spatial and temporal variability of the extremal dependence structure.
Several branches of computing use a system's physical dynamics to do computation. We show that the dynamics of an underdamped harmonic oscillator can perform multifunctional computation, solving distinct problems at distinct times within a dynamical trajectory. Oscillator computing usually focuses on the oscillator's phase as the information-carrying component. Here we focus on the time-resolved amplitude of an oscillator whose inputs influence its frequency, which has a natural parallel as the activity of a time-dependent neural unit. We call this unit an oscillatron. The activity of an oscillatron at fixed time is a nonmonotonic function of the input, and so it can solve nonlinearly-separable problems such as XOR. The activity of the oscillatron at fixed input is a nonmonotonic function of time, and so it is multifunctional in a temporal sense, able to carry out distinct nonlinear computations at distinct times within the same dynamical trajectory. Time-resolved computing of this nature can be done in or out of equilibrium, with the natural time evolution of the system giving us multiple computations for the price of one.
The remarkable practical success of deep learning has revealed some major surprises from a theoretical perspective. In particular, simple gradient methods easily find near-optimal solutions to non-convex optimization problems, and despite giving a near-perfect fit to training data without any explicit effort to control model complexity, these methods exhibit excellent predictive accuracy. We conjecture that specific principles underlie these phenomena: that overparametrization allows gradient methods to find interpolating solutions, that these methods implicitly impose regularization, and that overparametrization leads to benign overfitting. We survey recent theoretical progress that provides examples illustrating these principles in simpler settings. We first review classical uniform convergence results and why they fall short of explaining aspects of the behavior of deep learning methods. We give examples of implicit regularization in simple settings, where gradient methods lead to minimal norm functions that perfectly fit the training data. Then we review prediction methods that exhibit benign overfitting, focusing on regression problems with quadratic loss. For these methods, we can decompose the prediction rule into a simple component that is useful for prediction and a spiky component that is useful for overfitting but, in a favorable setting, does not harm prediction accuracy. We focus specifically on the linear regime for neural networks, where the network can be approximated by a linear model. In this regime, we demonstrate the success of gradient flow, and we consider benign overfitting with two-layer networks, giving an exact asymptotic analysis that precisely demonstrates the impact of overparametrization. We conclude by highlighting the key challenges that arise in extending these insights to realistic deep learning settings.
Graph representation learning for hypergraphs can be used to extract patterns among higher-order interactions that are critically important in many real world problems. Current approaches designed for hypergraphs, however, are unable to handle different types of hypergraphs and are typically not generic for various learning tasks. Indeed, models that can predict variable-sized heterogeneous hyperedges have not been available. Here we develop a new self-attention based graph neural network called Hyper-SAGNN applicable to homogeneous and heterogeneous hypergraphs with variable hyperedge sizes. We perform extensive evaluations on multiple datasets, including four benchmark network datasets and two single-cell Hi-C datasets in genomics. We demonstrate that Hyper-SAGNN significantly outperforms the state-of-the-art methods on traditional tasks while also achieving great performance on a new task called outsider identification. Hyper-SAGNN will be useful for graph representation learning to uncover complex higher-order interactions in different applications.