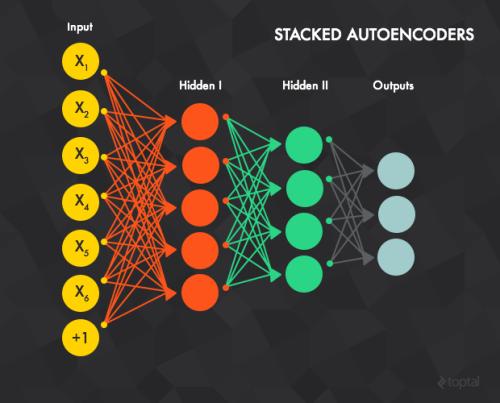
We propose a novel framework for the regularised inversion of deep neural networks. The framework is based on the authors' recent work on training feed-forward neural networks without the differentiation of activation functions. The framework lifts the parameter space into a higher dimensional space by introducing auxiliary variables, and penalises these variables with tailored Bregman distances. We propose a family of variational regularisations based on these Bregman distances, present theoretical results and support their practical application with numerical examples. In particular, we present the first convergence result (to the best of our knowledge) for the regularised inversion of a single-layer perceptron that only assumes that the solution of the inverse problem is in the range of the regularisation operator, and that shows that the regularised inverse provably converges to the true inverse if measurement errors converge to zero.
相關內容
神經網絡（Neural Networks）是世界上三個最古老的神經建模學會的檔案期刊:國際神經網絡學會(INNS)、歐洲神經網絡學會(ENNS)和日本神經網絡學會(JNNS)。神經網絡提供了一個論壇，以發展和培育一個國際社會的學者和實踐者感興趣的所有方面的神經網絡和相關方法的計算智能。神經網絡歡迎高質量論文的提交，有助于全面的神經網絡研究，從行為和大腦建模，學習算法，通過數學和計算分析，系統的工程和技術應用，大量使用神經網絡的概念和技術。這一獨特而廣泛的范圍促進了生物和技術研究之間的思想交流，并有助于促進對生物啟發的計算智能感興趣的跨學科社區的發展。因此，神經網絡編委會代表的專家領域包括心理學，神經生物學，計算機科學，工程，數學，物理。該雜志發表文章、信件和評論以及給編輯的信件、社論、時事、軟件調查和專利信息。文章發表在五個部分之一:認知科學，神經科學，學習系統，數學和計算分析、工程和應用。
官網地址：
Can we recover the hidden parameters of an Artificial Neural Network (ANN) by probing its input-output mapping? We propose a systematic method, called `Expand-and-Cluster' that needs only the number of hidden layers and the activation function of the probed ANN to identify all network parameters. In the expansion phase, we train a series of student networks of increasing size using the probed data of the ANN as a teacher. Expansion stops when a minimal loss is consistently reached in student networks of a given size. In the clustering phase, weight vectors of the expanded students are clustered, which allows structured pruning of superfluous neurons in a principled way. We find that an overparameterization of a factor four is sufficient to reliably identify the minimal number of neurons and to retrieve the original network parameters in $80\%$ of tasks across a family of 150 toy problems of variable difficulty. Furthermore, a teacher network trained on MNIST data can be identified with less than $5\%$ overhead in the neuron number. Thus, while direct training of a student network with a size identical to that of the teacher is practically impossible because of the non-convex loss function, training with mild overparameterization followed by clustering and structured pruning correctly identifies the target network.
In this paper, we consider Discretized Neural Networks (DNNs) consisting of low-precision weights and activations, which suffer from either infinite or zero gradients due to the non-differentiable discrete function in the training process. In this case, most training-based DNNs employ the standard Straight-Through Estimator (STE) to approximate the gradient w.r.t. discrete values. However, the STE gives rise to the problem of gradient mismatch, due to the perturbations of the approximated gradient. To address this problem, this paper reveals that this mismatch can be viewed as a metric perturbation in a Riemannian manifold through the lens of duality theory. Further, on the basis of the information geometry, we construct the Linearly Nearly Euclidean (LNE) manifold for DNNs as a background to deal with perturbations. By introducing a partial differential equation on metrics, i.e., the Ricci flow, we prove the dynamical stability and convergence of the LNE metric with the $L^2$-norm perturbation. Unlike the previous perturbation theory whose convergence rate is the fractional powers, the metric perturbation under the Ricci flow can be exponentially decayed in the LNE manifold. The experimental results on various datasets demonstrate that our method achieves better and more stable performance for DNNs than other representative training-based methods.
Graph neural networks (GNNs) are widely used for modeling complex interactions between entities represented as vertices of a graph. Despite recent efforts to theoretically analyze the expressive power of GNNs, a formal characterization of their ability to model interactions is lacking. The current paper aims to address this gap. Formalizing strength of interactions through an established measure known as separation rank, we quantify the ability of certain GNNs to model interaction between a given subset of vertices and its complement, i.e. between the sides of a given partition of input vertices. Our results reveal that the ability to model interaction is primarily determined by the partition's walk index -- a graph-theoretical characteristic defined by the number of walks originating from the boundary of the partition. Experiments with common GNN architectures corroborate this finding. As a practical application of our theory, we design an edge sparsification algorithm named Walk Index Sparsification (WIS), which preserves the ability of a GNN to model interactions when input edges are removed. WIS is simple, computationally efficient, and in our experiments has markedly outperformed alternative methods in terms of induced prediction accuracy. More broadly, it showcases the potential of improving GNNs by theoretically analyzing the interactions they can model.
Heterogeneous graphs offer powerful data representations for traffic, given their ability to model the complex interaction effects among a varying number of traffic participants and the underlying road infrastructure. With the recent advent of graph neural networks (GNNs) as the accompanying deep learning framework, the graph structure can be efficiently leveraged for various machine learning applications such as trajectory prediction. As a first of its kind, our proposed Python framework offers an easy-to-use and fully customizable data processing pipeline to extract standardized graph datasets from traffic scenarios. Providing a platform for GNN-based autonomous driving research, it improves comparability between approaches and allows researchers to focus on model implementation instead of dataset curation.
The Koopman operator provides a linear perspective on non-linear dynamics by focusing on the evolution of observables in an invariant subspace. Observables of interest are typically linearly reconstructed from the Koopman eigenfunctions. Despite the broad use of Koopman operators over the past few years, there exist some misconceptions about the applicability of Koopman operators to dynamical systems with more than one fixed point. In this work, an explanation is provided for the mechanism of lifting for the Koopman operator of a dynamical system with multiple attractors. Considering the example of the Duffing oscillator, we show that by exploiting the inherent symmetry between the basins of attraction, a linear reconstruction with three degrees of freedom in the Koopman observable space is sufficient to globally linearize the system.
This paper attempts to characterize the kinds of physical scenarios in which an online learning-based cognitive radar is expected to reliably outperform a fixed rule-based waveform selection strategy, as well as the converse. We seek general insights through an examination of two decision-making scenarios, namely dynamic spectrum access and multiple-target tracking. The radar scene is characterized by inducing a state-space model and examining the structure of its underlying Markov state transition matrix, in terms of entropy rate and diagonality. It is found that entropy rate is a strong predictor of online learning-based waveform selection, while diagonality is a better predictor of fixed rule-based waveform selection. We show that these measures can be used to predict first and second-order stochastic dominance relationships, which can allow system designers to make use of simple decision rules instead of more cumbersome learning approaches under certain conditions. We validate our findings through numerical results for each application and provide guidelines for future implementations.
This paper focuses on the expected difference in borrower's repayment when there is a change in the lender's credit decisions. Classical estimators overlook the confounding effects and hence the estimation error can be magnificent. As such, we propose another approach to construct the estimators such that the error can be greatly reduced. The proposed estimators are shown to be unbiased, consistent, and robust through a combination of theoretical analysis and numerical testing. Moreover, we compare the power of estimating the causal quantities between the classical estimators and the proposed estimators. The comparison is tested across a wide range of models, including linear regression models, tree-based models, and neural network-based models, under different simulated datasets that exhibit different levels of causality, different degrees of nonlinearity, and different distributional properties. Most importantly, we apply our approaches to a large observational dataset provided by a global technology firm that operates in both the e-commerce and the lending business. We find that the relative reduction of estimation error is strikingly substantial if the causal effects are accounted for correctly.
Incompleteness is a common problem for existing knowledge graphs (KGs), and the completion of KG which aims to predict links between entities is challenging. Most existing KG completion methods only consider the direct relation between nodes and ignore the relation paths which contain useful information for link prediction. Recently, a few methods take relation paths into consideration but pay less attention to the order of relations in paths which is important for reasoning. In addition, these path-based models always ignore nonlinear contributions of path features for link prediction. To solve these problems, we propose a novel KG completion method named OPTransE. Instead of embedding both entities of a relation into the same latent space as in previous methods, we project the head entity and the tail entity of each relation into different spaces to guarantee the order of relations in the path. Meanwhile, we adopt a pooling strategy to extract nonlinear and complex features of different paths to further improve the performance of link prediction. Experimental results on two benchmark datasets show that the proposed model OPTransE performs better than state-of-the-art methods.
Graph neural networks (GNNs) are a popular class of machine learning models whose major advantage is their ability to incorporate a sparse and discrete dependency structure between data points. Unfortunately, GNNs can only be used when such a graph-structure is available. In practice, however, real-world graphs are often noisy and incomplete or might not be available at all. With this work, we propose to jointly learn the graph structure and the parameters of graph convolutional networks (GCNs) by approximately solving a bilevel program that learns a discrete probability distribution on the edges of the graph. This allows one to apply GCNs not only in scenarios where the given graph is incomplete or corrupted but also in those where a graph is not available. We conduct a series of experiments that analyze the behavior of the proposed method and demonstrate that it outperforms related methods by a significant margin.
High spectral dimensionality and the shortage of annotations make hyperspectral image (HSI) classification a challenging problem. Recent studies suggest that convolutional neural networks can learn discriminative spatial features, which play a paramount role in HSI interpretation. However, most of these methods ignore the distinctive spectral-spatial characteristic of hyperspectral data. In addition, a large amount of unlabeled data remains an unexploited gold mine for efficient data use. Therefore, we proposed an integration of generative adversarial networks (GANs) and probabilistic graphical models for HSI classification. Specifically, we used a spectral-spatial generator and a discriminator to identify land cover categories of hyperspectral cubes. Moreover, to take advantage of a large amount of unlabeled data, we adopted a conditional random field to refine the preliminary classification results generated by GANs. Experimental results obtained using two commonly studied datasets demonstrate that the proposed framework achieved encouraging classification accuracy using a small number of data for training.
小貼士
登錄享
相關主題
注冊地址： 北京市海淀區羊坊店路18號2幢3層301-191