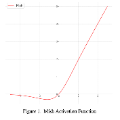
We investigate data-driven forward-inverse problems for Yajima-Oikawa (YO) system by employing two technologies which improve the performance of neural network in deep physics-informed neural network (PINN), namely neuron-wise locally adaptive activation functions and $L^2$ norm parameter regularization. Indeed, we not only recover three different forms of vector rogue waves (RWs) by means of three distinct initial-boundary value conditions in the forward problem of YO system, including bright-bright RWs, intermediate-bright RWs and dark-bright RWs, but also study the inverse problem of YO system by using training data with different noise intensity. In order to deal with the problem that the capacity of learning unknown parameters is not ideal when the PINN with only locally adaptive activation functions utilizes training data with noise interference in the inverse problem of YO system, thus we introduce $L^2$ norm regularization, which can drive the weights closer to origin, into PINN with locally adaptive activation functions, then find that the PINN model with two strategies shows amazing training effect by using training data with noise interference to investigate the inverse problem of YO system.
相關內容
The reinforcement learning (RL) problem is rife with sources of non-stationarity, making it a notoriously difficult problem domain for the application of neural networks. We identify a mechanism by which non-stationary prediction targets can prevent learning progress in deep RL agents: \textit{capacity loss}, whereby networks trained on a sequence of target values lose their ability to quickly update their predictions over time. We demonstrate that capacity loss occurs in a range of RL agents and environments, and is particularly damaging to performance in sparse-reward tasks. We then present a simple regularizer, Initial Feature Regularization (InFeR), that mitigates this phenomenon by regressing a subspace of features towards its value at initialization, leading to significant performance improvements in sparse-reward environments such as Montezuma's Revenge. We conclude that preventing capacity loss is crucial to enable agents to maximally benefit from the learning signals they obtain throughout the entire training trajectory.
We prove a central limit theorem for the entropic transportation cost between subgaussian probability measures, centered at the population cost. This is the first result which allows for asymptotically valid inference for entropic optimal transport between measures which are not necessarily discrete. In the compactly supported case, we complement these results with new, faster, convergence rates for the expected entropic transportation cost between empirical measures. Our proof is based on strengthening convergence results for dual solutions to the entropic optimal transport problem.
Deep neural networks have seen tremendous success over the last years. Since the training is performed on digital hardware, in this paper, we analyze what actually can be computed on current hardware platforms modeled as Turing machines, which would lead to inherent restrictions of deep learning. For this, we focus on the class of inverse problems, which, in particular, encompasses any task to reconstruct data from measurements. We prove that finite-dimensional inverse problems are not Banach-Mazur computable for small relaxation parameters. In fact, our result even holds for Borel-Turing computability., i.e., there does not exist an algorithm which performs the training of a neural network on digital hardware for any given accuracy. This establishes a conceptual barrier on the capabilities of neural networks for finite-dimensional inverse problems given that the computations are performed on digital hardware.
The problem of continuous inverse optimal control (over finite time horizon) is to learn the unknown cost function over the sequence of continuous control variables from expert demonstrations. In this article, we study this fundamental problem in the framework of energy-based model, where the observed expert trajectories are assumed to be random samples from a probability density function defined as the exponential of the negative cost function up to a normalizing constant. The parameters of the cost function are learned by maximum likelihood via an "analysis by synthesis" scheme, which iterates (1) synthesis step: sample the synthesized trajectories from the current probability density using the Langevin dynamics via back-propagation through time, and (2) analysis step: update the model parameters based on the statistical difference between the synthesized trajectories and the observed trajectories. Given the fact that an efficient optimization algorithm is usually available for an optimal control problem, we also consider a convenient approximation of the above learning method, where we replace the sampling in the synthesis step by optimization. Moreover, to make the sampling or optimization more efficient, we propose to train the energy-based model simultaneously with a top-down trajectory generator via cooperative learning, where the trajectory generator is used to fast initialize the synthesis step of the energy-based model. We demonstrate the proposed methods on autonomous driving tasks, and show that they can learn suitable cost functions for optimal control.
Binary pointwise labels (aka implicit feedback) are heavily leveraged by deep learning based recommendation algorithms nowadays. In this paper we discuss the limited expressiveness of these labels may fail to accommodate varying degrees of user preference, and thus lead to conflicts during model training, which we call annotation bias. To solve this issue, we find the soft-labeling property of pairwise labels could be utilized to alleviate the bias of pointwise labels. To this end, we propose a momentum contrast framework (MP2) that combines pointwise and pairwise learning for recommendation. MP2 has a three-tower network structure: one user network and two item networks. The two item networks are used for computing pointwise and pairwise loss respectively. To alleviate the influence of the annotation bias, we perform a momentum update to ensure a consistent item representation. Extensive experiments on real-world datasets demonstrate the superiority of our method against state-of-the-art recommendation algorithms.
In this paper, we propose a PAC-Bayesian \textit{a posteriori} parameter selection scheme for adaptive regularized regression in Hilbert scales under general, unknown source conditions. We demonstrate that our approach is adaptive to misspecification, and achieves the optimal learning rate under subgaussian noise. Unlike existing parameter selection schemes, the computational complexity of our approach is independent of sample size. We derive minimax adaptive rates for a new, broad class of Tikhonov-regularized learning problems under general, misspecified source conditions, that notably do not require any conventional a priori assumptions on kernel eigendecay. Using the theory of interpolation, we demonstrate that the spectrum of the Mercer operator can be inferred in the presence of "tight" $L^{\infty}$ embeddings of suitable Hilbert scales. Finally, we prove, that under a $\Delta_2$ condition on the smoothness index functions, our PAC-Bayesian scheme can indeed achieve minimax rates. We discuss applications of our approach to statistical inverse problems and oracle-efficient contextual bandit algorithms.
With the increasing penetration of distributed energy resources, distributed optimization algorithms have attracted significant attention for power systems applications due to their potential for superior scalability, privacy, and robustness to a single point-of-failure. The Alternating Direction Method of Multipliers (ADMM) is a popular distributed optimization algorithm; however, its convergence performance is highly dependent on the selection of penalty parameters, which are usually chosen heuristically. In this work, we use reinforcement learning (RL) to develop an adaptive penalty parameter selection policy for the AC optimal power flow (ACOPF) problem solved via ADMM with the goal of minimizing the number of iterations until convergence. We train our RL policy using deep Q-learning, and show that this policy can result in significantly accelerated convergence (up to a 59% reduction in the number of iterations compared to existing, curvature-informed penalty parameter selection methods). Furthermore, we show that our RL policy demonstrates promise for generalizability, performing well under unseen loading schemes as well as under unseen losses of lines and generators (up to a 50% reduction in iterations). This work thus provides a proof-of-concept for using RL for parameter selection in ADMM for power systems applications.
The adaptive processing of structured data is a long-standing research topic in machine learning that investigates how to automatically learn a mapping from a structured input to outputs of various nature. Recently, there has been an increasing interest in the adaptive processing of graphs, which led to the development of different neural network-based methodologies. In this thesis, we take a different route and develop a Bayesian Deep Learning framework for graph learning. The dissertation begins with a review of the principles over which most of the methods in the field are built, followed by a study on graph classification reproducibility issues. We then proceed to bridge the basic ideas of deep learning for graphs with the Bayesian world, by building our deep architectures in an incremental fashion. This framework allows us to consider graphs with discrete and continuous edge features, producing unsupervised embeddings rich enough to reach the state of the art on several classification tasks. Our approach is also amenable to a Bayesian nonparametric extension that automatizes the choice of almost all model's hyper-parameters. Two real-world applications demonstrate the efficacy of deep learning for graphs. The first concerns the prediction of information-theoretic quantities for molecular simulations with supervised neural models. After that, we exploit our Bayesian models to solve a malware-classification task while being robust to intra-procedural code obfuscation techniques. We conclude the dissertation with an attempt to blend the best of the neural and Bayesian worlds together. The resulting hybrid model is able to predict multimodal distributions conditioned on input graphs, with the consequent ability to model stochasticity and uncertainty better than most works. Overall, we aim to provide a Bayesian perspective into the articulated research field of deep learning for graphs.
The growing energy and performance costs of deep learning have driven the community to reduce the size of neural networks by selectively pruning components. Similarly to their biological counterparts, sparse networks generalize just as well, if not better than, the original dense networks. Sparsity can reduce the memory footprint of regular networks to fit mobile devices, as well as shorten training time for ever growing networks. In this paper, we survey prior work on sparsity in deep learning and provide an extensive tutorial of sparsification for both inference and training. We describe approaches to remove and add elements of neural networks, different training strategies to achieve model sparsity, and mechanisms to exploit sparsity in practice. Our work distills ideas from more than 300 research papers and provides guidance to practitioners who wish to utilize sparsity today, as well as to researchers whose goal is to push the frontier forward. We include the necessary background on mathematical methods in sparsification, describe phenomena such as early structure adaptation, the intricate relations between sparsity and the training process, and show techniques for achieving acceleration on real hardware. We also define a metric of pruned parameter efficiency that could serve as a baseline for comparison of different sparse networks. We close by speculating on how sparsity can improve future workloads and outline major open problems in the field.
Dynamic programming (DP) solves a variety of structured combinatorial problems by iteratively breaking them down into smaller subproblems. In spite of their versatility, DP algorithms are usually non-differentiable, which hampers their use as a layer in neural networks trained by backpropagation. To address this issue, we propose to smooth the max operator in the dynamic programming recursion, using a strongly convex regularizer. This allows to relax both the optimal value and solution of the original combinatorial problem, and turns a broad class of DP algorithms into differentiable operators. Theoretically, we provide a new probabilistic perspective on backpropagating through these DP operators, and relate them to inference in graphical models. We derive two particular instantiations of our framework, a smoothed Viterbi algorithm for sequence prediction and a smoothed DTW algorithm for time-series alignment. We showcase these instantiations on two structured prediction tasks and on structured and sparse attention for neural machine translation.