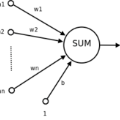
Quantum computing shows great potential, but errors pose a significant challenge. This study explores new strategies for mitigating quantum errors using artificial neural networks (ANN) and the Yang-Baxter equation (YBE). Unlike traditional error correction methods, which are computationally intensive, we investigate artificial error mitigation. The manuscript introduces the basics of quantum error sources and explores the potential of using classical computation for error mitigation. The Yang-Baxter equation plays a crucial role, allowing us to compress time dynamics simulations into constant-depth circuits. By introducing controlled noise through the YBE, we enhance the dataset for error mitigation. We train an ANN model on partial data from quantum simulations, demonstrating its effectiveness in correcting errors in time-evolving quantum states.
相關內容
Conformal inference is a popular tool for constructing prediction intervals (PI). We consider here the scenario of post-selection/selective conformal inference, that is PIs are reported only for individuals selected from an unlabeled test data. To account for multiplicity, we develop a general split conformal framework to construct selective PIs with the false coverage-statement rate (FCR) control. We first investigate the Benjamini and Yekutieli (2005)'s FCR-adjusted method in the present setting, and show that it is able to achieve FCR control but yields uniformly inflated PIs. We then propose a novel solution to the problem, named as Selective COnditional conformal Predictions (SCOP), which entails performing selection procedures on both calibration set and test set and construct marginal conformal PIs on the selected sets by the aid of conditional empirical distribution obtained by the calibration set. Under a unified framework and exchangeable assumptions, we show that the SCOP can exactly control the FCR. More importantly, we provide non-asymptotic miscoverage bounds for a general class of selection procedures beyond exchangeablity and discuss the conditions under which the SCOP is able to control the FCR. As special cases, the SCOP with quantile-based selection or conformal p-values-based multiple testing procedures enjoys valid coverage guarantee under mild conditions. Numerical results confirm the effectiveness and robustness of SCOP in FCR control and show that it achieves more narrowed PIs over existing methods in many settings.
This study proposes an interpretable neural network-based non-proportional odds model (N$^3$POM) for ordinal regression. N$^3$POM is different from conventional approaches to ordinal regression with non-proportional models in several ways: (1) N$^3$POM is defined for both continuous and discrete responses, whereas standard methods typically treat the ordered continuous variables as if they are discrete, (2) instead of estimating response-dependent finite-dimensional coefficients of linear models from discrete responses as is done in conventional approaches, we train a non-linear neural network to serve as a coefficient function. Thanks to the neural network, N$^3$POM offers flexibility while preserving the interpretability of conventional ordinal regression. We establish a sufficient condition under which the predicted conditional cumulative probability locally satisfies the monotonicity constraint over a user-specified region in the covariate space. Additionally, we provide a monotonicity-preserving stochastic (MPS) algorithm for effectively training the neural network. We apply N$^3$POM to several real-world datasets.
The tool mpbn offers a Python programming interface for an easy interactive editing of Boolean networks and the efficient computation of elementary properties of their dynamics, including fixed points, trap spaces, and reachability properties under the Most Permissive update mode. Relying on Answer-Set Programming logical framework, we show that mpbn is scalable to models with several thousands of nodes and is one of the best-performing tool for computing minimal and maximal trap spaces of Boolean networks, a key feature for understanding and controling their stable behaviors. The tool is available at //github.com/bnediction/mpbn.
Electrical circuits are present in a variety of technologies, making their design an important part of computer aided engineering. The growing number of parameters that affect the final design leads to a need for new approaches to quantify their impact. Machine learning may play a key role in this regard, however current approaches often make suboptimal use of existing knowledge about the system at hand. In terms of circuits, their description via modified nodal analysis is well-understood. This particular formulation leads to systems of differential-algebraic equations (DAEs) which bring with them a number of peculiarities, e.g. hidden constraints that the solution needs to fulfill. We use the recently introduced dissection index that can decouple a given system of DAEs into ordinary differential equations, only depending on differential variables, and purely algebraic equations, that describe the relations between differential and algebraic variables. The idea is to then only learn the differential variables and reconstruct the algebraic ones using the relations from the decoupling. This approach guarantees that the algebraic constraints are fulfilled up to the accuracy of the nonlinear system solver, and it may also reduce the learning effort as only the differential variables need to be learned.
This article is concerned with the multilevel Monte Carlo (MLMC) methods for approximating expectations of some functions of the solution to the Heston 3/2-model from mathematical finance, which takes values in $(0, \infty)$ and possesses superlinearly growing drift and diffusion coefficients. To discretize the SDE model, a new Milstein-type scheme is proposed to produce independent sample paths. The proposed scheme can be explicitly solved and is positivity-preserving unconditionally, i.e., for any time step-size $h>0$. This positivity-preserving property for large discretization time steps is particularly desirable in the MLMC setting. Furthermore, a mean-square convergence rate of order one is proved in the non-globally Lipschitz regime, which is not trivial, as the diffusion coefficient grows super-linearly. The obtained order-one convergence in turn promises the desired relevant variance of the multilevel estimator and justifies the optimal complexity $\mathcal{O}(\epsilon^{-2})$ for the MLMC approach, where $\epsilon > 0$ is the required target accuracy. Numerical experiments are finally reported to confirm the theoretical findings.
In this paper, we propose a new modified likelihood ratio test (LRT) for simultaneously testing mean vectors and covariance matrices of two-sample populations in high-dimensional settings. By employing tools from Random Matrix Theory (RMT), we derive the limiting null distribution of the modified LRT for generally distributed populations. Furthermore, we compare the proposed test with existing tests using simulation results, demonstrating that the modified LRT exhibits favorable properties in terms of both size and power.
The sparsity-ranked lasso (SRL) has been developed for model selection and estimation in the presence of interactions and polynomials. The main tenet of the SRL is that an algorithm should be more skeptical of higher-order polynomials and interactions *a priori* compared to main effects, and hence the inclusion of these more complex terms should require a higher level of evidence. In time series, the same idea of ranked prior skepticism can be applied to the possibly seasonal autoregressive (AR) structure of the series during the model fitting process, becoming especially useful in settings with uncertain or multiple modes of seasonality. The SRL can naturally incorporate exogenous variables, with streamlined options for inference and/or feature selection. The fitting process is quick even for large series with a high-dimensional feature set. In this work, we discuss both the formulation of this procedure and the software we have developed for its implementation via the **fastTS** R package. We explore the performance of our SRL-based approach in a novel application involving the autoregressive modeling of hourly emergency room arrivals at the University of Iowa Hospitals and Clinics. We find that the SRL is considerably faster than its competitors, while producing more accurate predictions.
This paper concerns an expansion of first-order Belnap-Dunn logic whose connectives and quantifiers are all familiar from classical logic. The language and logical consequence relation of the logic are defined, a proof system for the defined logic is presented, and the soundness and completeness of the presented proof system is established. The close relationship between the logical consequence relations of the defined logic and the version of classical logic with the same language is illustrated by the minor differences between the presented proof system and a sound and complete proof system for the version of classical logic with the same language. Moreover, fifteen classical laws of logical equivalence are given by which the logical equivalence relation of the defined logic distinguishes itself from the logical equivalence relation of many logics that are closely related at first glance.
The goal of explainable Artificial Intelligence (XAI) is to generate human-interpretable explanations, but there are no computationally precise theories of how humans interpret AI generated explanations. The lack of theory means that validation of XAI must be done empirically, on a case-by-case basis, which prevents systematic theory-building in XAI. We propose a psychological theory of how humans draw conclusions from saliency maps, the most common form of XAI explanation, which for the first time allows for precise prediction of explainee inference conditioned on explanation. Our theory posits that absent explanation humans expect the AI to make similar decisions to themselves, and that they interpret an explanation by comparison to the explanations they themselves would give. Comparison is formalized via Shepard's universal law of generalization in a similarity space, a classic theory from cognitive science. A pre-registered user study on AI image classifications with saliency map explanations demonstrate that our theory quantitatively matches participants' predictions of the AI.
While deep learning strategies achieve outstanding results in computer vision tasks, one issue remains. The current strategies rely heavily on a huge amount of labeled data. In many real-world problems it is not feasible to create such an amount of labeled training data. Therefore, researchers try to incorporate unlabeled data into the training process to reach equal results with fewer labels. Due to a lot of concurrent research, it is difficult to keep track of recent developments. In this survey we provide an overview of often used techniques and methods in image classification with fewer labels. We compare 21 methods. In our analysis we identify three major trends. 1. State-of-the-art methods are scaleable to real world applications based on their accuracy. 2. The degree of supervision which is needed to achieve comparable results to the usage of all labels is decreasing. 3. All methods share common techniques while only few methods combine these techniques to achieve better performance. Based on all of these three trends we discover future research opportunities.