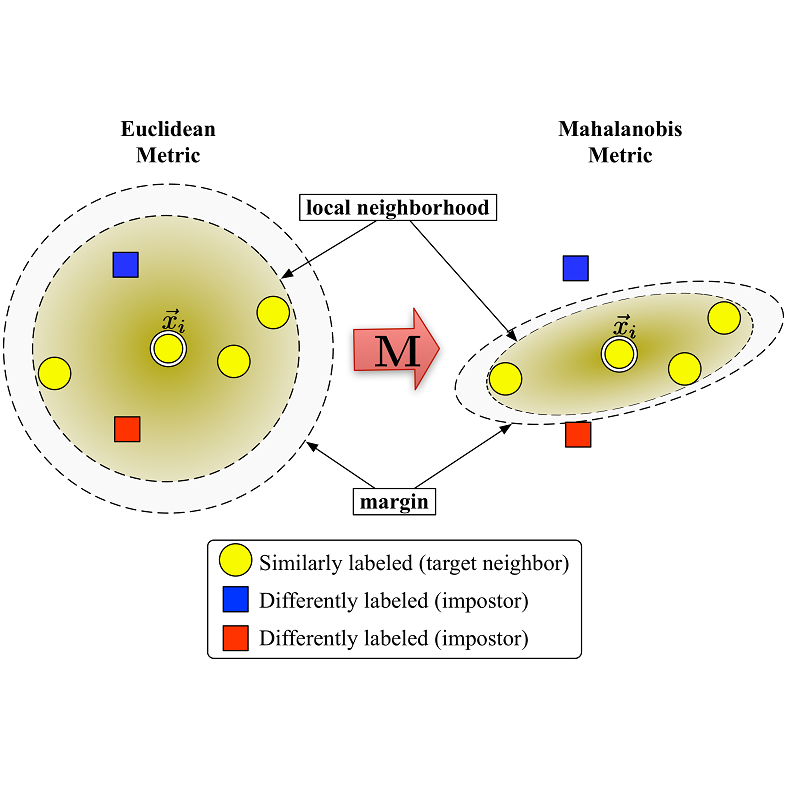
Deep metric learning (DML) is a cornerstone of many computer vision applications. It aims at learning a mapping from the input domain to an embedding space, where semantically similar objects are located nearby and dissimilar objects far from another. The target similarity on the training data is defined by user in form of ground-truth class labels. However, while the embedding space learns to mimic the user-provided similarity on the training data, it should also generalize to novel categories not seen during training. Besides user-provided groundtruth training labels, a lot of additional visual factors (such as viewpoint changes or shape peculiarities) exist and imply different notions of similarity between objects, affecting the generalization on the images unseen during training. However, existing approaches usually directly learn a single embedding space on all available training data, struggling to encode all different types of relationships, and do not generalize well. We propose to build a more expressive representation by jointly splitting the embedding space and the data hierarchically into smaller sub-parts. We successively focus on smaller subsets of the training data, reducing its variance and learning a different embedding subspace for each data subset. Moreover, the subspaces are learned jointly to cover not only the intricacies, but the breadth of the data as well. Only after that, we build the final embedding from the subspaces in the conquering stage. The proposed algorithm acts as a transparent wrapper that can be placed around arbitrary existing DML methods. Our approach significantly improves upon the state-of-the-art on image retrieval, clustering, and re-identification tasks evaluated using CUB200-2011, CARS196, Stanford Online Products, In-shop Clothes, and PKU VehicleID datasets.
相關內容
The goal of few-shot learning is to recognize new visual concepts with just a few amount of labeled samples in each class. Recent effective metric-based few-shot approaches employ neural networks to learn a feature similarity comparison between query and support examples. However, the importance of feature embedding, i.e., exploring the relationship among training samples, is neglected. In this work, we present a simple yet powerful baseline for few-shot classification by emphasizing the importance of feature embedding. Specifically, we revisit the classical triplet network from deep metric learning, and extend it into a deep K-tuplet network for few-shot learning, utilizing the relationship among the input samples to learn a general representation learning via episode-training. Once trained, our network is able to extract discriminative features for unseen novel categories and can be seamlessly incorporated with a non-linear distance metric function to facilitate the few-shot classification. Our result on the miniImageNet benchmark outperforms other metric-based few-shot classification methods. More importantly, when evaluated on completely different datasets (Caltech-101, CUB-200, Stanford Dogs and Cars) using the model trained with miniImageNet, our method significantly outperforms prior methods, demonstrating its superior capability to generalize to unseen classes.
Alternating Direction Method of Multipliers (ADMM) is a widely used tool for machine learning in distributed settings, where a machine learning model is trained over distributed data sources through an interactive process of local computation and message passing. Such an iterative process could cause privacy concerns of data owners. The goal of this paper is to provide differential privacy for ADMM-based distributed machine learning. Prior approaches on differentially private ADMM exhibit low utility under high privacy guarantee and often assume the objective functions of the learning problems to be smooth and strongly convex. To address these concerns, we propose a novel differentially private ADMM-based distributed learning algorithm called DP-ADMM, which combines an approximate augmented Lagrangian function with time-varying Gaussian noise addition in the iterative process to achieve higher utility for general objective functions under the same differential privacy guarantee. We also apply the moments accountant method to bound the end-to-end privacy loss. The theoretical analysis shows that DP-ADMM can be applied to a wider class of distributed learning problems, is provably convergent, and offers an explicit utility-privacy tradeoff. To our knowledge, this is the first paper to provide explicit convergence and utility properties for differentially private ADMM-based distributed learning algorithms. The evaluation results demonstrate that our approach can achieve good convergence and model accuracy under high end-to-end differential privacy guarantee.
This paper presents a hardness-aware deep metric learning (HDML) framework. Most previous deep metric learning methods employ the hard negative mining strategy to alleviate the lack of informative samples for training. However, this mining strategy only utilizes a subset of training data, which may not be enough to characterize the global geometry of the embedding space comprehensively. To address this problem, we perform linear interpolation on embeddings to adaptively manipulate their hard levels and generate corresponding label-preserving synthetics for recycled training, so that information buried in all samples can be fully exploited and the metric is always challenged with proper difficulty. Our method achieves very competitive performance on the widely used CUB-200-2011, Cars196, and Stanford Online Products datasets.
Learning embedding functions, which map semantically related inputs to nearby locations in a feature space supports a variety of classification and information retrieval tasks. In this work, we propose a novel, generalizable and fast method to define a family of embedding functions that can be used as an ensemble to give improved results. Each embedding function is learned by randomly bagging the training labels into small subsets. We show experimentally that these embedding ensembles create effective embedding functions. The ensemble output defines a metric space that improves state of the art performance for image retrieval on CUB-200-2011, Cars-196, In-Shop Clothes Retrieval and VehicleID.
Deep learning is the mainstream technique for many machine learning tasks, including image recognition, machine translation, speech recognition, and so on. It has outperformed conventional methods in various fields and achieved great successes. Unfortunately, the understanding on how it works remains unclear. It has the central importance to lay down the theoretic foundation for deep learning. In this work, we give a geometric view to understand deep learning: we show that the fundamental principle attributing to the success is the manifold structure in data, namely natural high dimensional data concentrates close to a low-dimensional manifold, deep learning learns the manifold and the probability distribution on it. We further introduce the concepts of rectified linear complexity for deep neural network measuring its learning capability, rectified linear complexity of an embedding manifold describing the difficulty to be learned. Then we show for any deep neural network with fixed architecture, there exists a manifold that cannot be learned by the network. Finally, we propose to apply optimal mass transportation theory to control the probability distribution in the latent space.
With the development of deep learning, Deep Metric Learning (DML) has achieved great improvements in face recognition. Specifically, the widely used softmax loss in the training process often bring large intra-class variations, and feature normalization is only exploited in the testing process to compute the pair similarities. To bridge the gap, we impose the intra-class cosine similarity between the features and weight vectors in softmax loss larger than a margin in the training step, and extend it from four aspects. First, we explore the effect of a hard sample mining strategy. To alleviate the human labor of adjusting the margin hyper-parameter, a self-adaptive margin updating strategy is proposed. Then, a normalized version is given to take full advantage of the cosine similarity constraint. Furthermore, we enhance the former constraint to force the intra-class cosine similarity larger than the mean inter-class cosine similarity with a margin in the exponential feature projection space. Extensive experiments on Labeled Face in the Wild (LFW), Youtube Faces (YTF) and IARPA Janus Benchmark A (IJB-A) datasets demonstrate that the proposed methods outperform the mainstream DML methods and approach the state-of-the-art performance.
Image segmentation needs both local boundary position information and global object context information. The performance of the recent state-of-the-art method, fully convolutional networks, reaches a bottleneck due to the neural network limit after balancing between the two types of information simultaneously in an end-to-end training style. To overcome this problem, we divide the semantic image segmentation into temporal subtasks. First, we find a possible pixel position of some object boundary; then trace the boundary at steps within a limited length until the whole object is outlined. We present the first deep reinforcement learning approach to semantic image segmentation, called DeepOutline, which outperforms other algorithms in Coco detection leaderboard in the middle and large size person category in Coco val2017 dataset. Meanwhile, it provides an insight into a divide and conquer way by reinforcement learning on computer vision problems.
Recently, ensemble has been applied to deep metric learning to yield state-of-the-art results. Deep metric learning aims to learn deep neural networks for feature embeddings, distances of which satisfy given constraint. In deep metric learning, ensemble takes average of distances learned by multiple learners. As one important aspect of ensemble, the learners should be diverse in their feature embeddings. To this end, we propose an attention-based ensemble, which uses multiple attention masks, so that each learner can attend to different parts of the object. We also propose a divergence loss, which encourages diversity among the learners. The proposed method is applied to the standard benchmarks of deep metric learning and experimental results show that it outperforms the state-of-the-art methods by a significant margin on image retrieval tasks.
Deep distance metric learning (DDML), which is proposed to learn image similarity metrics in an end-to-end manner based on the convolution neural network, has achieved encouraging results in many computer vision tasks.$L2$-normalization in the embedding space has been used to improve the performance of several DDML methods. However, the commonly used Euclidean distance is no longer an accurate metric for $L2$-normalized embedding space, i.e., a hyper-sphere. Another challenge of current DDML methods is that their loss functions are usually based on rigid data formats, such as the triplet tuple. Thus, an extra process is needed to prepare data in specific formats. In addition, their losses are obtained from a limited number of samples, which leads to a lack of the global view of the embedding space. In this paper, we replace the Euclidean distance with the cosine similarity to better utilize the $L2$-normalization, which is able to attenuate the curse of dimensionality. More specifically, a novel loss function based on the von Mises-Fisher distribution is proposed to learn a compact hyper-spherical embedding space. Moreover, a new efficient learning algorithm is developed to better capture the global structure of the embedding space. Experiments for both classification and retrieval tasks on several standard datasets show that our method achieves state-of-the-art performance with a simpler training procedure. Furthermore, we demonstrate that, even with a small number of convolutional layers, our model can still obtain significantly better classification performance than the widely used softmax loss.
Several machine learning models, including neural networks, consistently misclassify adversarial examples---inputs formed by applying small but intentionally worst-case perturbations to examples from the dataset, such that the perturbed input results in the model outputting an incorrect answer with high confidence. Early attempts at explaining this phenomenon focused on nonlinearity and overfitting. We argue instead that the primary cause of neural networks' vulnerability to adversarial perturbation is their linear nature. This explanation is supported by new quantitative results while giving the first explanation of the most intriguing fact about them: their generalization across architectures and training sets. Moreover, this view yields a simple and fast method of generating adversarial examples. Using this approach to provide examples for adversarial training, we reduce the test set error of a maxout network on the MNIST dataset.