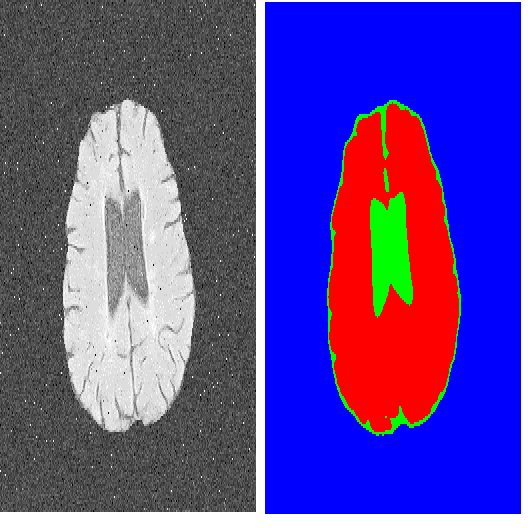
Current dataset mask processing operations relies on interpolation algorithms that do not produce extra pixels, such as nearest neighbor (NN) interpolation, as opposed to algorithms that do produce extra pixels, like bicubic (BIC) or bilinear (BIL) interpolation. In our previous study, the author proposed an alternative approach to NN-based mask processing and evaluated its effects on deep learning training outcomes. In this study, the author evaluated the effects of both BIC-based image and mask processing and BIC-and-NN-based image and mask processing versus NN-based image and mask processing. The evaluation revealed that the BIC-BIC model/network was an 8.9578 % (with image size 256 x 256) and a 1.0496 % (with image size 384 x 384) increase of the NN-NN network compared to the NN-BIC network which was an 8.3127 % (with image size 256 x 256) and a 0.2887 % (with image size 384 x 384) increase of the NN-NN network.
相關內容
Traditional clustering algorithms often struggle to capture the complex relationships within graphs and generalise to arbitrary clustering criteria. The emergence of graph neural networks (GNNs) as a powerful framework for learning representations of graph data provides new approaches to solving the problem. Previous work has shown GNNs to be capable of proposing partitionings using a variety of criteria, however, these approaches have not yet been extended to work on Markov chains or kinetic networks. These arise frequently in the study of molecular systems and are of particular interest to the biochemical modelling community. In this work, we propose several GNN-based architectures to tackle the graph partitioning problem for Markov Chains described as kinetic networks. This approach aims to minimize how much a proposed partitioning changes the Kemeny constant. We propose using an encoder-decoder architecture and show how simple GraphSAGE-based GNNs with linear layers can outperform much larger and more expressive attention-based models in this context. As a proof of concept, we first demonstrate the method's ability to cluster randomly connected graphs. We also use a linear chain architecture corresponding to a 1D free energy profile as our kinetic network. Subsequently, we demonstrate the effectiveness of our method through experiments on a data set derived from molecular dynamics. We compare the performance of our method to other partitioning techniques such as PCCA+. We explore the importance of feature and hyperparameter selection and propose a general strategy for large-scale parallel training of GNNs for discovering optimal graph partitionings.
Multiphysics incompressible fluid dynamics simulations play a crucial role in understanding intricate behaviors of many complex engineering systems that involve interactions between solids, fluids, and various phases like liquid and gas. Numerical modeling of these interactions has generated significant research interest in recent decades and has led to the development of open source simulation tools and commercial software products targeting specific applications or general problem classes in computational fluid dynamics. As the demand increases for these simulations to adapt to platform heterogeneity, ensure composability between different physics models, and effectively utilize inheritance within partial differentiation systems, a fundamental reconsideration of numerical solver design becomes imperative. The discussion presented in this paper emphasizes the importance of these considerations and introduces the Flash-X approach as a potential solution. The software design strategies outlined in the article serve as a guide for Flash-X developers, providing insights into complexities associated with performance portability, composability, and sustainable development. These strategies provide a foundation for improving design of both new and existing simulation tools grappling with these challenges. By incorporating the principles outlined in the Flash-X approach, engineers and researchers can enhance the adaptability, efficiency, and overall effectiveness of their numerical solvers in the ever-evolving field of multiphysics simulations.
Traditional clustering algorithms often struggle to capture the complex relationships within graphs and generalise to arbitrary clustering criteria. The emergence of graph neural networks (GNNs) as a powerful framework for learning representations of graph data provides new approaches to solving the problem. Previous work has shown GNNs to be capable of proposing partitionings using a variety of criteria, however, these approaches have not yet been extended to work on Markov chains or kinetic networks. These arise frequently in the study of molecular systems and are of particular interest to the biochemical modelling community. In this work, we propose several GNN-based architectures to tackle the graph partitioning problem for Markov Chains described as kinetic networks. This approach aims to minimize how much a proposed partitioning changes the Kemeny constant. We propose using an encoder-decoder architecture and show how simple GraphSAGE-based GNNs with linear layers can outperform much larger and more expressive attention-based models in this context. As a proof of concept, we first demonstrate the method's ability to cluster randomly connected graphs. We also use a linear chain architecture corresponding to a 1D free energy profile as our kinetic network. Subsequently, we demonstrate the effectiveness of our method through experiments on a data set derived from molecular dynamics. We compare the performance of our method to other partitioning techniques such as PCCA+. We explore the importance of feature and hyperparameter selection and propose a general strategy for large-scale parallel training of GNNs for discovering optimal graph partitionings.
This paper explores the application diffusion maps as graph shift operators in understanding the underlying geometry of graph signals. The study evaluates the improvements in graph learning when using diffusion map generated filters to the Markov Variation minimization problem. The paper showcases the effectiveness of this approach through examples involving synthetically generated and real-world temperature sensor data. These examples also compare the diffusion map graph signal model with other commonly used graph signal operators. The results provide new approaches for the analysis and understanding of complex, non-Euclidean data structures.
The quantum communication cost of computing a classical sum of distributed sources is studied over a quantum erasure multiple access channel (QEMAC). $K$ classical messages are distributed across $S$ servers, who also share quantum entanglement in advance. Each server $s\in[S]$ manipulates and sends its quantum subsystem $\mathcal{Q}_s$ to the receiver who computes the sum of the messages. The download cost from Server $s\in [S]$ is the logarithm of the dimension of $\mathcal{Q}_s$. The rate $R$ is defined as the number of instances of the sum computed at the receiver, divided by the total download cost from all the servers. In the symmetric setting with $K= {S \choose \alpha} $ messages where each message is replicated among a unique subset of $\alpha$ servers, and the answers from any $\beta$ servers may be erased, we show that the capacity (maximal rate) is $C= \max\left\{ \min \left\{ \frac{2(\alpha-\beta)}{S}, \frac{S-2\beta}{S} \right\}, \frac{\alpha-\beta}{S} \right\}$.

The existence of representative datasets is a prerequisite of many successful artificial intelligence and machine learning models. However, the subsequent application of these models often involves scenarios that are inadequately represented in the data used for training. The reasons for this are manifold and range from time and cost constraints to ethical considerations. As a consequence, the reliable use of these models, especially in safety-critical applications, is a huge challenge. Leveraging additional, already existing sources of knowledge is key to overcome the limitations of purely data-driven approaches, and eventually to increase the generalization capability of these models. Furthermore, predictions that conform with knowledge are crucial for making trustworthy and safe decisions even in underrepresented scenarios. This work provides an overview of existing techniques and methods in the literature that combine data-based models with existing knowledge. The identified approaches are structured according to the categories integration, extraction and conformity. Special attention is given to applications in the field of autonomous driving.
As soon as abstract mathematical computations were adapted to computation on digital computers, the problem of efficient representation, manipulation, and communication of the numerical values in those computations arose. Strongly related to the problem of numerical representation is the problem of quantization: in what manner should a set of continuous real-valued numbers be distributed over a fixed discrete set of numbers to minimize the number of bits required and also to maximize the accuracy of the attendant computations? This perennial problem of quantization is particularly relevant whenever memory and/or computational resources are severely restricted, and it has come to the forefront in recent years due to the remarkable performance of Neural Network models in computer vision, natural language processing, and related areas. Moving from floating-point representations to low-precision fixed integer values represented in four bits or less holds the potential to reduce the memory footprint and latency by a factor of 16x; and, in fact, reductions of 4x to 8x are often realized in practice in these applications. Thus, it is not surprising that quantization has emerged recently as an important and very active sub-area of research in the efficient implementation of computations associated with Neural Networks. In this article, we survey approaches to the problem of quantizing the numerical values in deep Neural Network computations, covering the advantages/disadvantages of current methods. With this survey and its organization, we hope to have presented a useful snapshot of the current research in quantization for Neural Networks and to have given an intelligent organization to ease the evaluation of future research in this area.
High spectral dimensionality and the shortage of annotations make hyperspectral image (HSI) classification a challenging problem. Recent studies suggest that convolutional neural networks can learn discriminative spatial features, which play a paramount role in HSI interpretation. However, most of these methods ignore the distinctive spectral-spatial characteristic of hyperspectral data. In addition, a large amount of unlabeled data remains an unexploited gold mine for efficient data use. Therefore, we proposed an integration of generative adversarial networks (GANs) and probabilistic graphical models for HSI classification. Specifically, we used a spectral-spatial generator and a discriminator to identify land cover categories of hyperspectral cubes. Moreover, to take advantage of a large amount of unlabeled data, we adopted a conditional random field to refine the preliminary classification results generated by GANs. Experimental results obtained using two commonly studied datasets demonstrate that the proposed framework achieved encouraging classification accuracy using a small number of data for training.
Image segmentation is an important component of many image understanding systems. It aims to group pixels in a spatially and perceptually coherent manner. Typically, these algorithms have a collection of parameters that control the degree of over-segmentation produced. It still remains a challenge to properly select such parameters for human-like perceptual grouping. In this work, we exploit the diversity of segments produced by different choices of parameters. We scan the segmentation parameter space and generate a collection of image segmentation hypotheses (from highly over-segmented to under-segmented). These are fed into a cost minimization framework that produces the final segmentation by selecting segments that: (1) better describe the natural contours of the image, and (2) are more stable and persistent among all the segmentation hypotheses. We compare our algorithm's performance with state-of-the-art algorithms, showing that we can achieve improved results. We also show that our framework is robust to the choice of segmentation kernel that produces the initial set of hypotheses.
While it is nearly effortless for humans to quickly assess the perceptual similarity between two images, the underlying processes are thought to be quite complex. Despite this, the most widely used perceptual metrics today, such as PSNR and SSIM, are simple, shallow functions, and fail to account for many nuances of human perception. Recently, the deep learning community has found that features of the VGG network trained on the ImageNet classification task has been remarkably useful as a training loss for image synthesis. But how perceptual are these so-called "perceptual losses"? What elements are critical for their success? To answer these questions, we introduce a new Full Reference Image Quality Assessment (FR-IQA) dataset of perceptual human judgments, orders of magnitude larger than previous datasets. We systematically evaluate deep features across different architectures and tasks and compare them with classic metrics. We find that deep features outperform all previous metrics by huge margins. More surprisingly, this result is not restricted to ImageNet-trained VGG features, but holds across different deep architectures and levels of supervision (supervised, self-supervised, or even unsupervised). Our results suggest that perceptual similarity is an emergent property shared across deep visual representations.