亚洲男人的天堂2018av,欧美草比,久久久久久免费视频精选,国色天香在线看免费,久久久久亚洲av成人片仓井空

Neural networks of ads systems usually take input from multiple resources, e.g., query-ad relevance, ad features and user portraits. These inputs are encoded into one-hot or multi-hot binary features, with typically only a tiny fraction of nonzero feature values per example. Deep learning models in online advertising industries can have terabyte-scale parameters that do not fit in the GPU memory nor the CPU main memory on a computing node. For example, a sponsored online advertising system can contain more than $10^{11}$ sparse features, making the neural network a massive model with around 10 TB parameters. In this paper, we introduce a distributed GPU hierarchical parameter server for massive scale deep learning ads systems. We propose a hierarchical workflow that utilizes GPU High-Bandwidth Memory, CPU main memory and SSD as 3-layer hierarchical storage. All the neural network training computations are contained in GPUs. Extensive experiments on real-world data confirm the effectiveness and the scalability of the proposed system. A 4-node hierarchical GPU parameter server can train a model more than 2X faster than a 150-node in-memory distributed parameter server in an MPI cluster. In addition, the price-performance ratio of our proposed system is 4-9 times better than an MPI-cluster solution.

Learning embedding functions, which map semantically related inputs to nearby locations in a feature space supports a variety of classification and information retrieval tasks. In this work, we propose a novel, generalizable and fast method to define a family of embedding functions that can be used as an ensemble to give improved results. Each embedding function is learned by randomly bagging the training labels into small subsets. We show experimentally that these embedding ensembles create effective embedding functions. The ensemble output defines a metric space that improves state of the art performance for image retrieval on CUB-200-2011, Cars-196, In-Shop Clothes Retrieval and VehicleID.

Tracking by detection is a common approach to solving the Multiple Object Tracking problem. In this paper we show how deep metric learning can be used to improve three aspects of tracking by detection. We train a convolutional neural network to learn an embedding function in a Siamese configuration on a large person re-identification dataset offline. It is then used to improve the online performance of tracking while retaining a high frame rate. We use this learned appearance metric to robustly build estimates of pedestrian's trajectories in the MOT16 dataset. In breaking with the tracking by detection model, we use our appearance metric to propose detections using the predicted state of a tracklet as a prior in the case where the detector fails. This method achieves competitive results in evaluation, especially among online, real-time approaches. We present an ablative study showing the impact of each of the three uses of our deep appearance metric.

Deep learning is the mainstream technique for many machine learning tasks, including image recognition, machine translation, speech recognition, and so on. It has outperformed conventional methods in various fields and achieved great successes. Unfortunately, the understanding on how it works remains unclear. It has the central importance to lay down the theoretic foundation for deep learning. In this work, we give a geometric view to understand deep learning: we show that the fundamental principle attributing to the success is the manifold structure in data, namely natural high dimensional data concentrates close to a low-dimensional manifold, deep learning learns the manifold and the probability distribution on it. We further introduce the concepts of rectified linear complexity for deep neural network measuring its learning capability, rectified linear complexity of an embedding manifold describing the difficulty to be learned. Then we show for any deep neural network with fixed architecture, there exists a manifold that cannot be learned by the network. Finally, we propose to apply optimal mass transportation theory to control the probability distribution in the latent space.

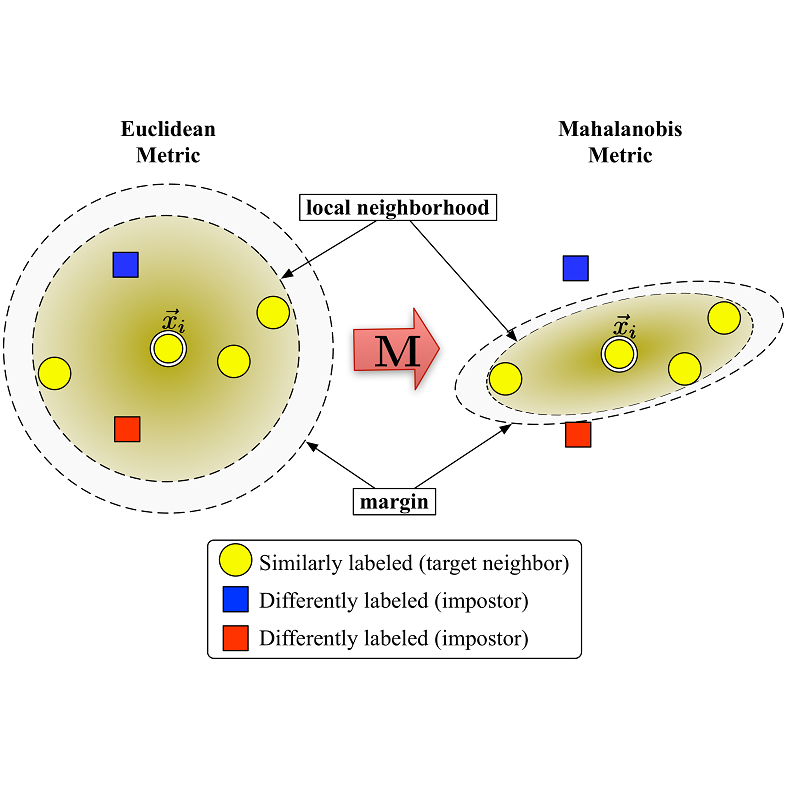
Metric learning learns a metric function from training data to calculate the similarity or distance between samples. From the perspective of feature learning, metric learning essentially learns a new feature space by feature transformation (e.g., Mahalanobis distance metric). However, traditional metric learning algorithms are shallow, which just learn one metric space (feature transformation). Can we further learn a better metric space from the learnt metric space? In other words, can we learn metric progressively and nonlinearly like deep learning by just using the existing metric learning algorithms? To this end, we present a hierarchical metric learning scheme and implement an online deep metric learning framework, namely ODML. Specifically, we take one online metric learning algorithm as a metric layer, followed by a nonlinear layer (i.e., ReLU), and then stack these layers modelled after the deep learning. The proposed ODML enjoys some nice properties, indeed can learn metric progressively and performs superiorly on some datasets. Various experiments with different settings have been conducted to verify these properties of the proposed ODML.

Similarity/Distance measures play a key role in many machine learning, pattern recognition, and data mining algorithms, which leads to the emergence of metric learning field. Many metric learning algorithms learn a global distance function from data that satisfy the constraints of the problem. However, in many real-world datasets that the discrimination power of features varies in the different regions of input space, a global metric is often unable to capture the complexity of the task. To address this challenge, local metric learning methods are proposed that learn multiple metrics across the different regions of input space. Some advantages of these methods are high flexibility and the ability to learn a nonlinear mapping but typically achieves at the expense of higher time requirement and overfitting problem. To overcome these challenges, this research presents an online multiple metric learning framework. Each metric in the proposed framework is composed of a global and a local component learned simultaneously. Adding a global component to a local metric efficiently reduce the problem of overfitting. The proposed framework is also scalable with both sample size and the dimension of input data. To the best of our knowledge, this is the first local online similarity/distance learning framework based on PA (Passive/Aggressive). In addition, for scalability with the dimension of input data, DRP (Dual Random Projection) is extended for local online learning in the present work. It enables our methods to be run efficiently on high-dimensional datasets, while maintains their predictive performance. The proposed framework provides a straightforward local extension to any global online similarity/distance learning algorithm based on PA.

Deep metric learning has been demonstrated to be highly effective in learning semantic representation and encoding information that can be used to measure data similarity, by relying on the embedding learned from metric learning. At the same time, variational autoencoder (VAE) has widely been used to approximate inference and proved to have a good performance for directed probabilistic models. However, for traditional VAE, the data label or feature information are intractable. Similarly, traditional representation learning approaches fail to represent many salient aspects of the data. In this project, we propose a novel integrated framework to learn latent embedding in VAE by incorporating deep metric learning. The features are learned by optimizing a triplet loss on the mean vectors of VAE in conjunction with standard evidence lower bound (ELBO) of VAE. This approach, which we call Triplet based Variational Autoencoder (TVAE), allows us to capture more fine-grained information in the latent embedding. Our model is tested on MNIST data set and achieves a high triplet accuracy of 95.60% while the traditional VAE (Kingma & Welling, 2013) achieves triplet accuracy of 75.08%.

Recently, ensemble has been applied to deep metric learning to yield state-of-the-art results. Deep metric learning aims to learn deep neural networks for feature embeddings, distances of which satisfy given constraint. In deep metric learning, ensemble takes average of distances learned by multiple learners. As one important aspect of ensemble, the learners should be diverse in their feature embeddings. To this end, we propose an attention-based ensemble, which uses multiple attention masks, so that each learner can attend to different parts of the object. We also propose a divergence loss, which encourages diversity among the learners. The proposed method is applied to the standard benchmarks of deep metric learning and experimental results show that it outperforms the state-of-the-art methods by a significant margin on image retrieval tasks.

Deep distance metric learning (DDML), which is proposed to learn image similarity metrics in an end-to-end manner based on the convolution neural network, has achieved encouraging results in many computer vision tasks.$L2$-normalization in the embedding space has been used to improve the performance of several DDML methods. However, the commonly used Euclidean distance is no longer an accurate metric for $L2$-normalized embedding space, i.e., a hyper-sphere. Another challenge of current DDML methods is that their loss functions are usually based on rigid data formats, such as the triplet tuple. Thus, an extra process is needed to prepare data in specific formats. In addition, their losses are obtained from a limited number of samples, which leads to a lack of the global view of the embedding space. In this paper, we replace the Euclidean distance with the cosine similarity to better utilize the $L2$-normalization, which is able to attenuate the curse of dimensionality. More specifically, a novel loss function based on the von Mises-Fisher distribution is proposed to learn a compact hyper-spherical embedding space. Moreover, a new efficient learning algorithm is developed to better capture the global structure of the embedding space. Experiments for both classification and retrieval tasks on several standard datasets show that our method achieves state-of-the-art performance with a simpler training procedure. Furthermore, we demonstrate that, even with a small number of convolutional layers, our model can still obtain significantly better classification performance than the widely used softmax loss.

Interest point descriptors have fueled progress on almost every problem in computer vision. Recent advances in deep neural networks have enabled task-specific learned descriptors that outperform hand-crafted descriptors on many problems. We demonstrate that commonly used metric learning approaches do not optimally leverage the feature hierarchies learned in a Convolutional Neural Network (CNN), especially when applied to the task of geometric feature matching. While a metric loss applied to the deepest layer of a CNN, is often expected to yield ideal features irrespective of the task, in fact the growing receptive field as well as striding effects cause shallower features to be better at high precision matching tasks. We leverage this insight together with explicit supervision at multiple levels of the feature hierarchy for better regularization, to learn more effective descriptors in the context of geometric matching tasks. Further, we propose to use activation maps at different layers of a CNN, as an effective and principled replacement for the multi-resolution image pyramids often used for matching tasks. We propose concrete CNN architectures employing these ideas, and evaluate them on multiple datasets for 2D and 3D geometric matching as well as optical flow, demonstrating state-of-the-art results and generalization across datasets.