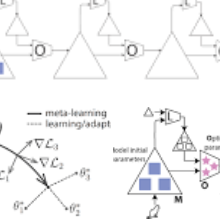
We analyse a general class of bilevel problems, in which the upper-level problem consists in the minimization of a smooth objective function and the lower-level problem is to find the fixed point of a smooth contraction map. This type of problems include instances of meta-learning, equilibrium models, hyperparameter optimization and data poisoning adversarial attacks. Several recent works have proposed algorithms which warm-start the lower-level problem, i.e. they use the previous lower-level approximate solution as a staring point for the lower-level solver. This warm-start procedure allows one to improve the sample complexity in both the stochastic and deterministic settings, achieving in some cases the order-wise optimal sample complexity. However, there are situations, e.g., meta learning and equilibrium models, in which the warm-start procedure is not well-suited or ineffective. In this work we show that without warm-start, it is still possible to achieve order-wise (near) optimal sample complexity. In particular, we propose a simple method which uses (stochastic) fixed point iterations at the lower-level and projected inexact gradient descent at the upper-level, that reaches an $\epsilon$-stationary point using $O(\epsilon^{-2})$ and $\tilde{O}(\epsilon^{-1})$ samples for the stochastic and the deterministic setting, respectively. Finally, compared to methods using warm-start, our approach yields a simpler analysis that does not need to study the coupled interactions between the upper-level and lower-level iterates.
相關內容
In relational verification, judicious alignment of computational steps facilitates proof of relations between programs using simple relational assertions. Relational Hoare logics (RHL) provide compositional rules that embody various alignments of executions. Seemingly more flexible alignments can be expressed in terms of product automata based on program transition relations. A single degenerate alignment rule (self-composition), atop a complete Hoare logic, comprises a RHL for $\forall\forall$ properties that is complete in the ordinary logical sense. The notion of alignment completeness was previously proposed as a more satisfactory measure, and some rules were shown to be alignment complete with respect to a few ad hoc forms of alignment automata. This paper proves alignment completeness with respect to a general class of $\forall\forall$ alignment automata, for a RHL comprised of standard rules together with a rule of semantics-preserving rewrites based on Kleene algebra with tests. We also give a new logic for $\forall\exists$ properties and prove its alignment completeness.
Recommender systems are a ubiquitous feature of online platforms. Increasingly, they are explicitly tasked with increasing users' long-term satisfaction. In this context, we study a content exploration task, which we formalize as a multi-armed bandit problem with delayed rewards. We observe that there is an apparent trade-off in choosing the learning signal: Waiting for the full reward to become available might take several weeks, hurting the rate at which learning happens, whereas measuring short-term proxy rewards reflects the actual long-term goal only imperfectly. We address this challenge in two steps. First, we develop a predictive model of delayed rewards that incorporates all information obtained to date. Full observations as well as partial (short or medium-term) outcomes are combined through a Bayesian filter to obtain a probabilistic belief. Second, we devise a bandit algorithm that takes advantage of this new predictive model. The algorithm quickly learns to identify content aligned with long-term success by carefully balancing exploration and exploitation. We apply our approach to a podcast recommendation problem, where we seek to identify shows that users engage with repeatedly over two months. We empirically validate that our approach results in substantially better performance compared to approaches that either optimize for short-term proxies, or wait for the long-term outcome to be fully realized.
Information about action costs is critical for real-world AI planning applications. Rather than rely solely on declarative action models, recent approaches also use black-box external action cost estimators, often learned from data, that are applied during the planning phase. These, however, can be computationally expensive, and produce uncertain values. In this paper we suggest a generalization of deterministic planning with action costs that allows selecting between multiple estimators for action cost, to balance computation time against bounded estimation uncertainty. This enables a much richer -- and correspondingly more realistic -- problem representation. Importantly, it allows planners to bound plan accuracy, thereby increasing reliability, while reducing unnecessary computational burden, which is critical for scaling to large problems. We introduce a search algorithm, generalizing $A^*$, that solves such planning problems, and additional algorithmic extensions. In addition to theoretical guarantees, extensive experiments show considerable savings in runtime compared to alternatives.
In an earlier paper (//doi.org/10.1137/21M1393315), the Switch Point Algorithm was developed for solving optimal control problems whose solutions are either singular or bang-bang or both singular and bang-bang, and which possess a finite number of jump discontinuities in an optimal control at the points in time where the solution structure changes. The class of control problems that were considered had a given initial condition, but no terminal constraint. The theory is now extended to include problems with both initial and terminal constraints, a structure that often arises in boundary-value problems. Substantial changes to the theory are needed to handle this more general setting. Nonetheless, the derivative of the cost with respect to a switch point is again the jump in the Hamiltonian at the switch point.
In this paper we derive tight lower bounds resolving the hardness status of several fundamental weighted matroid problems. One notable example is budgeted matroid independent set, for which we show there is no fully polynomial-time approximation scheme (FPTAS), indicating the Efficient PTAS of [Doron-Arad, Kulik and Shachnai, SOSA 2023] is the best possible. Furthermore, we show that there is no pseudo-polynomial time algorithm for exact weight matroid independent set, implying the algorithm of [Camerini, Galbiati and Maffioli, J. Algorithms 1992] for representable matroids cannot be generalized to arbitrary matroids. Similarly, we show there is no Fully PTAS for constrained minimum basis of a matroid and knapsack cover with a matroid, implying the existing Efficient PTAS for the former is optimal. For all of the above problems, we obtain unconditional lower bounds in the oracle model, where the independent sets of the matroid can be accessed only via a membership oracle. We complement these results by showing that the same lower bounds hold under standard complexity assumptions, even if the matroid is encoded as part of the instance. All of our bounds are based on a specifically structured family of paving matroids.
We study the mixing time of the single-site update Markov chain, known as the Glauber dynamics, for generating a random independent set of a tree. Our focus is obtaining optimal convergence results for arbitrary trees. We consider the more general problem of sampling from the Gibbs distribution in the hard-core model where independent sets are weighted by a parameter $\lambda>0$. Previous work of Martinelli, Sinclair and Weitz (2004) obtained optimal mixing time bounds for the complete $\Delta$-regular tree for all $\lambda$. However, Restrepo et al. (2014) showed that for sufficiently large $\lambda$ there are bounded-degree trees where optimal mixing does not hold. Recent work of Eppstein and Frishberg (2022) proved a polynomial mixing time bound for the Glauber dynamics for arbitrary trees, and more generally for graphs of bounded tree-width. We establish an optimal bound on the relaxation time (i.e., inverse spectral gap) of $O(n)$ for the Glauber dynamics for unweighted independent sets on arbitrary trees. Moreover, for $\lambda\leq .44$ we prove an optimal mixing time bound of $O(n\log{n})$. We stress that our results hold for arbitrary trees and there is no dependence on the maximum degree $\Delta$. Interestingly, our results extend (far) beyond the uniqueness threshold which is on the order $\lambda=O(1/\Delta)$. Our proof approach is inspired by recent work on spectral independence. In fact, we prove that spectral independence holds with a constant independent of the maximum degree for any tree, but this does not imply mixing for general trees as the optimal mixing results of Chen, Liu, and Vigoda (2021) only apply for bounded degree graphs. We instead utilize the combinatorial nature of independent sets to directly prove approximate tensorization of variance/entropy via a non-trivial inductive proof.
Algorithms for online learning typically require one or more boundedness assumptions: that the domain is bounded, that the losses are Lipschitz, or both. In this paper, we develop a new setting for online learning with unbounded domains and non-Lipschitz losses. For this setting we provide an algorithm which guarantees $R_{T}(u)\le \tilde O(G\|u\|\sqrt{T}+L\|u\|^{2}\sqrt{T})$ regret on any problem where the subgradients satisfy $\|g_{t}\|\le G+L\|w_{t}\|$, and show that this bound is unimprovable without further assumptions. We leverage this algorithm to develop new saddle-point optimization algorithms that converge in duality gap in unbounded domains, even in the absence of meaningful curvature. Finally, we provide the first algorithm achieving non-trivial dynamic regret in an unbounded domain for non-Lipschitz losses, as well as a matching lower bound. The regret of our dynamic regret algorithm automatically improves to a novel $L^{*}$ bound when the losses are smooth.
We study the fundamental problem of fairly allocating a set of indivisible goods among $n$ agents with additive valuations using the desirable fairness notion of maximin share (MMS). MMS is the most popular share-based notion, in which an agent finds an allocation fair to her if she receives goods worth at least her MMS value. An allocation is called MMS if all agents receive at least their MMS value. However, since MMS allocations need not exist when $n>2$, a series of works showed the existence of approximate MMS allocations with the current best factor of $\frac{3}{4} + O(\frac{1}{n})$. The recent work by Akrami et al. showed the limitations of existing approaches and proved that they cannot improve this factor to $3/4 + \Omega(1)$. In this paper, we bypass these barriers to show the existence of $(\frac{3}{4} + \frac{3}{3836})$-MMS allocations by developing new reduction rules and analysis techniques.
We present a combination technique based on mixed differences of both spatial approximations and quadrature formulae for the stochastic variables to solve efficiently a class of Optimal Control Problems (OCPs) constrained by random partial differential equations. The method requires to solve the OCP for several low-fidelity spatial grids and quadrature formulae for the objective functional. All the computed solutions are then linearly combined to get a final approximation which, under suitable regularity assumptions, preserves the same accuracy of fine tensor product approximations, while drastically reducing the computational cost. The combination technique involves only tensor product quadrature formulae, thus the discretized OCPs preserve the convexity of the continuous OCP. Hence, the combination technique avoids the inconveniences of Multilevel Monte Carlo and/or sparse grids approaches, but remains suitable for high dimensional problems. The manuscript presents an a-priori procedure to choose the most important mixed differences and an asymptotic complexity analysis, which states that the asymptotic complexity is exclusively determined by the spatial solver. Numerical experiments validate the results.
A mainstream type of current self-supervised learning methods pursues a general-purpose representation that can be well transferred to downstream tasks, typically by optimizing on a given pretext task such as instance discrimination. In this work, we argue that existing pretext tasks inevitably introduce biases into the learned representation, which in turn leads to biased transfer performance on various downstream tasks. To cope with this issue, we propose Maximum Entropy Coding (MEC), a more principled objective that explicitly optimizes on the structure of the representation, so that the learned representation is less biased and thus generalizes better to unseen downstream tasks. Inspired by the principle of maximum entropy in information theory, we hypothesize that a generalizable representation should be the one that admits the maximum entropy among all plausible representations. To make the objective end-to-end trainable, we propose to leverage the minimal coding length in lossy data coding as a computationally tractable surrogate for the entropy, and further derive a scalable reformulation of the objective that allows fast computation. Extensive experiments demonstrate that MEC learns a more generalizable representation than previous methods based on specific pretext tasks. It achieves state-of-the-art performance consistently on various downstream tasks, including not only ImageNet linear probe, but also semi-supervised classification, object detection, instance segmentation, and object tracking. Interestingly, we show that existing batch-wise and feature-wise self-supervised objectives could be seen equivalent to low-order approximations of MEC. Code and pre-trained models are available at //github.com/xinliu20/MEC.