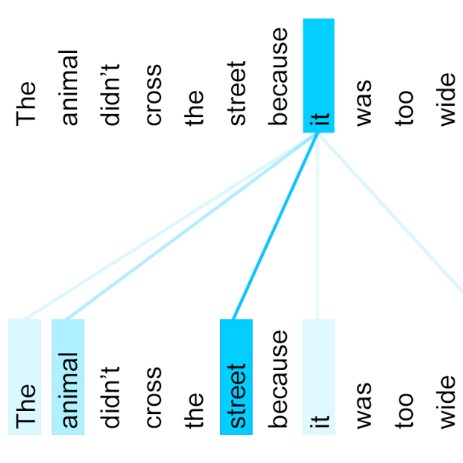
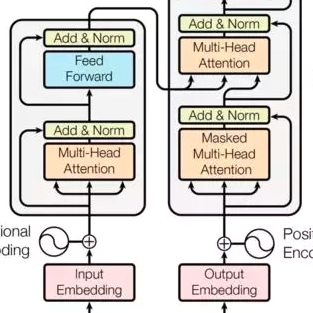
In this paper, we apply the self-attention from the state-of-the-art Transformer in Attention Is All You Need for the first time to a data-driven operator learning problem related to partial differential equations. An effort is put together to explain the heuristics of, and to improve the efficacy of the attention mechanism. By employing the operator approximation theory in Hilbert spaces, it is demonstrated for the first time that the softmax normalization in the scaled dot-product attention is sufficient but not necessary. Without softmax, the approximation capacity of a linearized Transformer variant can be proved to be comparable to a Petrov-Galerkin projection layer-wise, and the estimate is independent with respect to the sequence length. A new layer normalization scheme mimicking the Petrov-Galerkin projection is proposed to allow a scaling to propagate through attention layers, which helps the model achieve remarkable accuracy in operator learning tasks with unnormalized data. Finally, we present three operator learning experiments, including the viscid Burgers' equation, an interface Darcy flow, and an inverse interface coefficient identification problem. The newly proposed simple attention-based operator learner, Galerkin Transformer, shows significant improvements in both training cost and evaluation accuracy over its softmax-normalized counterparts.
相關內容
Let $\bx_j = \btheta +\bep_j, j=1,...,n$, be observations of an unknown parameter $\btheta$ in a Euclidean or separable Hilbert space $\scrH$, where $\bep_j$ are noises as random elements in $\scrH$ from a general distribution. We study the estimation of $f(\btheta)$ for a given functional $f:\scrH\rightarrow \RR$ based on $\bx_j$'s. The key element of our approach is a new method which we call High-Order Degenerate Statistical Expansion. It leverages the use of classical multivariate Taylor expansion and degenerate $U$-statistic and yields an elegant explicit formula. In the univariate case of $\scrH=\R$, the formula expresses the error of the proposed estimator as a sum of order $k$ degenerate $U$-products of the noises with coefficient $f^{(k)}(\btheta)/k!$ and an explicit remainder term in the form of the Riemann-Liouville integral as in the Taylor expansion around the true $\btheta$. For general $\scrH$, the formula expresses the estimation error in terms of the inner product of $f^{(k)}(\btheta)/k!$ and the average of the tensor products of $k$ noises with distinct indices and a parallel extension of the remainder term from the univariate case. This makes the proposed method a natural statistical version of the classical Taylor expansion. The proposed estimator can be viewed as a jackknife estimator of an ideal degenerate expansion of $f(\cdot)$ around the true $\btheta$ with the degenerate $U$-product of the noises, and can be approximated by bootstrap. Thus, the jackknife, bootstrap and Taylor expansion approaches all converge to the proposed estimator. We develop risk bounds for the proposed estimator and a central limit theorem under a second moment condition (even in expansions of higher than the second order). We apply this new method to generalize several existing results with smooth and nonsmooth $f$ to universal $\bep_j$'s with only minimum moment constraints.
We study a fourth-order div problem and its approximation by the discontinuous Petrov-Galerkin method with optimal test functions. We present two variants, based on first and second-order systems. In both cases we prove well-posedness of the formulation and quasi-optimal convergence of the approximation. Our analysis includes the fully-discrete schemes with approximated test functions, for general dimension and polynomial degree in the first-order case, and for two dimensions and lowest-order approximation in the second-order case. Numerical results illustrate the performance for quasi-uniform and adaptively refined meshes.
This paper offers a new approach to address the model uncertainty in (potentially) divergent-dimensional single-index models (SIMs). We propose a model-averaging estimator based on cross-validation, which allows the dimension of covariates and the number of candidate models to increase with the sample size. We show that when all candidate models are misspecified, our model-averaging estimator is asymptotically optimal in the sense that its squared loss is asymptotically identical to that of the infeasible best possible averaging estimator. In a different situation where correct models are available in the model set, the proposed weighting scheme assigns all weights to the correct models in the asymptotic sense. We also extend our method to average regularized estimators and propose pre-screening methods to deal with cases with high-dimensional covariates. We illustrate the merits of our method via simulations and two empirical applications.
Iterative hard thresholding (IHT) has gained in popularity over the past decades in large-scale optimization. However, convergence properties of this method have only been explored recently in non-convex settings. In matrix completion, existing works often focus on the guarantee of global convergence of IHT via standard assumptions such as incoherence property and uniform sampling. While such analysis provides a global upper bound on the linear convergence rate, it does not describe the actual performance of IHT in practice. In this paper, we provide a novel insight into the local convergence of a specific variant of IHT for matrix completion. We uncover the exact linear rate of IHT in a closed-form expression and identify the region of convergence in which the algorithm is guaranteed to converge. Furthermore, we utilize random matrix theory to study the linear rate of convergence of IHTSVD for large-scale matrix completion. We find that asymptotically, the rate can be expressed in closed form in terms of the relative rank and the sampling rate. Finally, we present various numerical results to verify the aforementioned theoretical analysis.
In this paper, we study deep neural networks (DNNs) for solving high-dimensional evolution equations with oscillatory solutions. Different from deep least-squares methods that deal with time and space variables simultaneously, we propose a deep adaptive basis Galerkin (DABG) method which employs the spectral-Galerkin method for time variable by tensor-product basis for oscillatory solutions and the deep neural network method for high-dimensional space variables. The proposed method can lead to a linear system of differential equations having unknown DNNs that can be trained via the loss function. We establish a posterior estimates of the solution error which is bounded by the minimal loss function and the term $O(N^{-m})$, where $N$ is the number of basis functions and $m$ characterizes the regularity of the equation, and show that if the true solution is a Barron-type function, the error bound converges to zero as $M=O(N^p)$ approaches to infinity where $M$ is the width of the used networks and $p$ is a positive constant. Numerical examples including high-dimensional linear parabolic and hyperbolic equations, and nonlinear Allen-Cahn equation are presented to demonstrate the performance of the proposed DABG method is better than that of existing DNNs.
This paper focuses on the regularization of backward time-fractional diffusion problem on unbounded domain. This problem is well-known to be ill-posed, whence the need of a regularization method in order to recover stable approximate solution. For the problem under consideration, we present a unified framework of regularization which covers some techniques such as Fourier regularization [19], mollification [12] and approximate-inverse [7]. We investigate a regularization technique with two major advantages: the simplicity of computation of the regularized solution and the avoid of truncation of high frequency components (so as to avoid undesirable oscillation on the resulting approximate-solution). Under classical Sobolev-smoothness conditions, we derive order-optimal error estimates between the approximate solution and the exact solution in the case where both the data and the model are only approximately known. In addition, an order-optimal a-posteriori parameter choice rule based on the Morozov principle is given. Finally, via some numerical experiments in two-dimensional space, we illustrate the efficiency of our regularization approach and we numerically confirm the theoretical convergence rates established in the paper.
Non-convex optimization is ubiquitous in modern machine learning. Researchers devise non-convex objective functions and optimize them using off-the-shelf optimizers such as stochastic gradient descent and its variants, which leverage the local geometry and update iteratively. Even though solving non-convex functions is NP-hard in the worst case, the optimization quality in practice is often not an issue -- optimizers are largely believed to find approximate global minima. Researchers hypothesize a unified explanation for this intriguing phenomenon: most of the local minima of the practically-used objectives are approximately global minima. We rigorously formalize it for concrete instances of machine learning problems.
In this paper, we focus on the problem of applying the transformer structure to video captioning effectively. The vanilla transformer is proposed for uni-modal language generation task such as machine translation. However, video captioning is a multimodal learning problem, and the video features have much redundancy between different time steps. Based on these concerns, we propose a novel method called sparse boundary-aware transformer (SBAT) to reduce the redundancy in video representation. SBAT employs boundary-aware pooling operation for scores from multihead attention and selects diverse features from different scenarios. Also, SBAT includes a local correlation scheme to compensate for the local information loss brought by sparse operation. Based on SBAT, we further propose an aligned cross-modal encoding scheme to boost the multimodal interaction. Experimental results on two benchmark datasets show that SBAT outperforms the state-of-the-art methods under most of the metrics.
Importance sampling is one of the most widely used variance reduction strategies in Monte Carlo rendering. In this paper, we propose a novel importance sampling technique that uses a neural network to learn how to sample from a desired density represented by a set of samples. Our approach considers an existing Monte Carlo rendering algorithm as a black box. During a scene-dependent training phase, we learn to generate samples with a desired density in the primary sample space of the rendering algorithm using maximum likelihood estimation. We leverage a recent neural network architecture that was designed to represent real-valued non-volume preserving ('Real NVP') transformations in high dimensional spaces. We use Real NVP to non-linearly warp primary sample space and obtain desired densities. In addition, Real NVP efficiently computes the determinant of the Jacobian of the warp, which is required to implement the change of integration variables implied by the warp. A main advantage of our approach is that it is agnostic of underlying light transport effects, and can be combined with many existing rendering techniques by treating them as a black box. We show that our approach leads to effective variance reduction in several practical scenarios.
Dynamic programming (DP) solves a variety of structured combinatorial problems by iteratively breaking them down into smaller subproblems. In spite of their versatility, DP algorithms are usually non-differentiable, which hampers their use as a layer in neural networks trained by backpropagation. To address this issue, we propose to smooth the max operator in the dynamic programming recursion, using a strongly convex regularizer. This allows to relax both the optimal value and solution of the original combinatorial problem, and turns a broad class of DP algorithms into differentiable operators. Theoretically, we provide a new probabilistic perspective on backpropagating through these DP operators, and relate them to inference in graphical models. We derive two particular instantiations of our framework, a smoothed Viterbi algorithm for sequence prediction and a smoothed DTW algorithm for time-series alignment. We showcase these instantiations on two structured prediction tasks and on structured and sparse attention for neural machine translation.