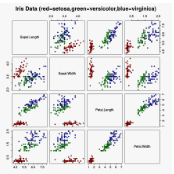
There are various cluster validity measures used for evaluating clustering results. One of the main objective of using these measures is to seek the optimal unknown number of clusters. Some measures work well for clusters with different densities, sizes and shapes. Yet, one of the weakness that those validity measures share is that they sometimes provide only one clear optimal number of clusters. That number is actually unknown and there might be more than one potential sub-optimal options that a user may wish to choose based on different applications. We develop two new cluster validity indices based on a correlation between an actual distance between a pair of data points and a centroid distance of clusters that the two points locate in. Our proposed indices constantly yield several peaks at different numbers of clusters which overcome the weakness previously stated. Furthermore, the introduced correlation can also be used for evaluating the quality of a selected clustering result. Several experiments in different scenarios including the well-known iris data set and a real-world marketing application have been conducted in order to compare the proposed validity indices with several well-known ones.
相關內容
Majority-SAT is the problem of determining whether an input $n$-variable formula in conjunctive normal form (CNF) has at least $2^{n-1}$ satisfying assignments. Majority-SAT and related problems have been studied extensively in various AI communities interested in the complexity of probabilistic planning and inference. Although Majority-SAT has been known to be PP-complete for over 40 years, the complexity of a natural variant has remained open: Majority-$k$SAT, where the input CNF formula is restricted to have clause width at most $k$. We prove that for every $k$, Majority-$k$SAT is in P. In fact, for any positive integer $k$ and rational $\rho \in (0,1)$ with bounded denominator, we give an algorithm that can determine whether a given $k$-CNF has at least $\rho \cdot 2^n$ satisfying assignments, in deterministic linear time (whereas the previous best-known algorithm ran in exponential time). Our algorithms have interesting positive implications for counting complexity and the complexity of inference, significantly reducing the known complexities of related problems such as E-MAJ-$k$SAT and MAJ-MAJ-$k$SAT. At the heart of our approach is an efficient method for solving threshold counting problems by extracting sunflowers found in the corresponding set system of a $k$-CNF. We also show that the tractability of Majority-$k$SAT is somewhat fragile. For the closely related GtMajority-SAT problem (where we ask whether a given formula has greater than $2^{n-1}$ satisfying assignments) which is known to be PP-complete, we show that GtMajority-$k$SAT is in P for $k\le 3$, but becomes NP-complete for $k\geq 4$. These results are counterintuitive, because the ``natural'' classifications of these problems would have been PP-completeness, and because there is a stark difference in the complexity of GtMajority-$k$SAT and Majority-$k$SAT for all $k\ge 4$.
Population-wide screening to identify and isolate infectious individuals is a powerful tool for controlling COVID-19 and other infectious diseases. Testing an entire population, however, requires significant resources. Group testing can enable large-scale screening by testing more people with fewer resources, but dilution degrades its sensitivity, reducing its effectiveness as an infection control measure. Analysis of this tradeoff typically assumes that pooled samples are independent. Building on recent empirical results in the literature, we argue that this assumption significantly underestimates the true benefits of group testing. Indeed, placing samples from a social group or household into the same pool correlates a pool's samples. As a result, a positive pool likely contains multiple positive samples, increasing a pooled test's sensitivity and also tending to reduce the number of pools that require follow-up tests. We prove that under a general correlation structure, pooling correlated samples together ("correlated pooling") achieves higher sensitivity and requires fewer tests per positive identified compared to independently pooling the samples ("naive pooling") using the same pool size within the two-stage Dorfman procedure, the most widely-used group testing method. To the best of our knowledge, our work is the first to theoretically characterize correlation's effect on sensitivity, and the first to study its effect on test usage under a realistic test error model. Under a representative starting prevalence of 1%, simulation results estimate that correlated pooling requires 12.9% fewer tests than naive pooling to control an epidemic. Thus, we argue that correlation is an important consideration for policy-makers designing infection control interventions: it makes screening more attractive for infection control and it suggests that sample collection should maximize correlation.
Sequences with low aperiodic autocorrelation and crosscorrelation are used in communications and remote sensing. Golay and Shapiro independently devised a recursive construction that produces families of complementary pairs of binary sequences. In the simplest case, the construction produces the Rudin-Shapiro sequences, and in general it produces what we call Golay-Rudin-Shapiro sequences. Calculations by Littlewood show that the Rudin-Shapiro sequences have low mean square autocorrelation. A sequence's peak sidelobe level is its largest magnitude of autocorrelation over all nonzero shifts. H{\o}holdt, Jensen, and Justesen showed that there is some undetermined positive constant $A$ such that the peak sidelobe level of a Rudin-Shapiro sequence of length $2^n$ is bounded above by $A(1.842626\ldots)^n$, where $1.842626\ldots$ is the positive real root of $X^4-3 X-6$. We show that the peak sidelobe level is bounded above by $5(1.658967\ldots)^{n-4}$, where $1.658967\ldots$ is the real root of $X^3+X^2-2 X-4$. Any exponential bound with lower base will fail to be true for almost all $n$, and any bound with the same base but a lower constant prefactor will fail to be true for at least one $n$. We provide a similar bound on the peak crosscorrelation (largest magnitude of crosscorrelation over all shifts) between the sequences in each Rudin-Shapiro pair. The methods that we use generalize to all families of complementary pairs produced by the Golay-Rudin-Shapiro recursion, for which we obtain bounds on the peak sidelobe level and peak crosscorrelation with the same exponential growth rate as we obtain for the original Rudin-Shapiro sequences.
Spectral clustering (SC) is a popular clustering technique to find strongly connected communities on a graph. SC can be used in Graph Neural Networks (GNNs) to implement pooling operations that aggregate nodes belonging to the same cluster. However, the eigendecomposition of the Laplacian is expensive and, since clustering results are graph-specific, pooling methods based on SC must perform a new optimization for each new sample. In this paper, we propose a graph clustering approach that addresses these limitations of SC. We formulate a continuous relaxation of the normalized minCUT problem and train a GNN to compute cluster assignments that minimize this objective. Our GNN-based implementation is differentiable, does not require to compute the spectral decomposition, and learns a clustering function that can be quickly evaluated on out-of-sample graphs. From the proposed clustering method, we design a graph pooling operator that overcomes some important limitations of state-of-the-art graph pooling techniques and achieves the best performance in several supervised and unsupervised tasks.
Question answering over knowledge graphs (KGQA) has evolved from simple single-fact questions to complex questions that require graph traversal and aggregation. We propose a novel approach for complex KGQA that uses unsupervised message passing, which propagates confidence scores obtained by parsing an input question and matching terms in the knowledge graph to a set of possible answers. First, we identify entity, relationship, and class names mentioned in a natural language question, and map these to their counterparts in the graph. Then, the confidence scores of these mappings propagate through the graph structure to locate the answer entities. Finally, these are aggregated depending on the identified question type. This approach can be efficiently implemented as a series of sparse matrix multiplications mimicking joins over small local subgraphs. Our evaluation results show that the proposed approach outperforms the state-of-the-art on the LC-QuAD benchmark. Moreover, we show that the performance of the approach depends only on the quality of the question interpretation results, i.e., given a correct relevance score distribution, our approach always produces a correct answer ranking. Our error analysis reveals correct answers missing from the benchmark dataset and inconsistencies in the DBpedia knowledge graph. Finally, we provide a comprehensive evaluation of the proposed approach accompanied with an ablation study and an error analysis, which showcase the pitfalls for each of the question answering components in more detail.
We present a new clustering method in the form of a single clustering equation that is able to directly discover groupings in the data. The main proposition is that the first neighbor of each sample is all one needs to discover large chains and finding the groups in the data. In contrast to most existing clustering algorithms our method does not require any hyper-parameters, distance thresholds and/or the need to specify the number of clusters. The proposed algorithm belongs to the family of hierarchical agglomerative methods. The technique has a very low computational overhead, is easily scalable and applicable to large practical problems. Evaluation on well known datasets from different domains ranging between 1077 and 8.1 million samples shows substantial performance gains when compared to the existing clustering techniques.
Open Information Extraction (OpenIE) methods extract (noun phrase, relation phrase, noun phrase) triples from text, resulting in the construction of large Open Knowledge Bases (Open KBs). The noun phrases (NPs) and relation phrases in such Open KBs are not canonicalized, leading to the storage of redundant and ambiguous facts. Recent research has posed canonicalization of Open KBs as clustering over manuallydefined feature spaces. Manual feature engineering is expensive and often sub-optimal. In order to overcome this challenge, we propose Canonicalization using Embeddings and Side Information (CESI) - a novel approach which performs canonicalization over learned embeddings of Open KBs. CESI extends recent advances in KB embedding by incorporating relevant NP and relation phrase side information in a principled manner. Through extensive experiments on multiple real-world datasets, we demonstrate CESI's effectiveness.
Clustering is an essential data mining tool that aims to discover inherent cluster structure in data. For most applications, applying clustering is only appropriate when cluster structure is present. As such, the study of clusterability, which evaluates whether data possesses such structure, is an integral part of cluster analysis. However, methods for evaluating clusterability vary radically, making it challenging to select a suitable measure. In this paper, we perform an extensive comparison of measures of clusterability and provide guidelines that clustering users can reference to select suitable measures for their applications.
Many question answering systems over knowledge graphs rely on entity and relation linking components in order to connect the natural language input to the underlying knowledge graph. Traditionally, entity linking and relation linking have been performed either as dependent sequential tasks or as independent parallel tasks. In this paper, we propose a framework called EARL, which performs entity linking and relation linking as a joint task. EARL implements two different solution strategies for which we provide a comparative analysis in this paper: The first strategy is a formalisation of the joint entity and relation linking tasks as an instance of the Generalised Travelling Salesman Problem (GTSP). In order to be computationally feasible, we employ approximate GTSP solvers. The second strategy uses machine learning in order to exploit the connection density between nodes in the knowledge graph. It relies on three base features and re-ranking steps in order to predict entities and relations. We compare the strategies and evaluate them on a dataset with 5000 questions. Both strategies significantly outperform the current state-of-the-art approaches for entity and relation linking.
Knowledge Graph Embedding methods aim at representing entities and relations in a knowledge base as points or vectors in a continuous vector space. Several approaches using embeddings have shown promising results on tasks such as link prediction, entity recommendation, question answering, and triplet classification. However, only a few methods can compute low-dimensional embeddings of very large knowledge bases. In this paper, we propose KG2Vec, a novel approach to Knowledge Graph Embedding based on the skip-gram model. Instead of using a predefined scoring function, we learn it relying on Long Short-Term Memories. We evaluated the goodness of our embeddings on knowledge graph completion and show that KG2Vec is comparable to the quality of the scalable state-of-the-art approaches and can process large graphs by parsing more than a hundred million triples in less than 6 hours on common hardware.