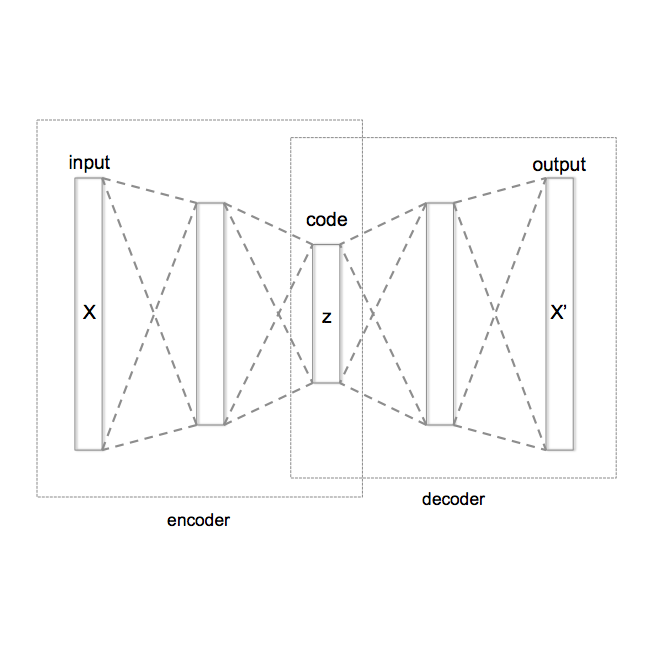
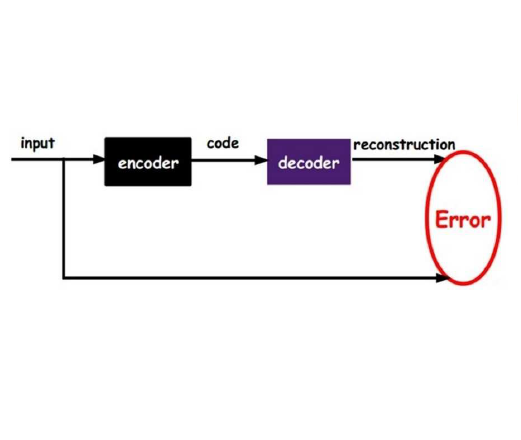
The Gaussianity assumption has been consistently criticized as a main limitation of the Variational Autoencoder (VAE) despite its efficiency in computational modeling. In this paper, we propose a new approach that expands the model capacity (i.e., expressive power of distributional family) without sacrificing the computational advantages of the VAE framework. Our VAE model's decoder is composed of an infinite mixture of asymmetric Laplace distribution, which possesses general distribution fitting capabilities for continuous variables. Our model is represented by a special form of a nonparametric M-estimator for estimating general quantile functions, and we theoretically establish the relevance between the proposed model and quantile estimation. We apply the proposed model to synthetic data generation, and particularly, our model demonstrates superiority in easily adjusting the level of data privacy.
相關內容
3D simulated environments play a critical role in Embodied AI, but their creation requires expertise and extensive manual effort, restricting their diversity and scope. To mitigate this limitation, we present Holodeck, a system that generates 3D environments to match a user-supplied prompt fully automatedly. Holodeck can generate diverse scenes, e.g., arcades, spas, and museums, adjust the designs for styles, and can capture the semantics of complex queries such as "apartment for a researcher with a cat" and "office of a professor who is a fan of Star Wars". Holodeck leverages a large language model (GPT-4) for common sense knowledge about what the scene might look like and uses a large collection of 3D assets from Objaverse to populate the scene with diverse objects. To address the challenge of positioning objects correctly, we prompt GPT-4 to generate spatial relational constraints between objects and then optimize the layout to satisfy those constraints. Our large-scale human evaluation shows that annotators prefer Holodeck over manually designed procedural baselines in residential scenes and that Holodeck can produce high-quality outputs for diverse scene types. We also demonstrate an exciting application of Holodeck in Embodied AI, training agents to navigate in novel scenes like music rooms and daycares without human-constructed data, which is a significant step forward in developing general-purpose embodied agents.
We present a novel method, the Chain of Empathy (CoE) prompting, that utilizes insights from psychotherapy to induce Large Language Models (LLMs) to reason about human emotional states. This method is inspired by various psychotherapy approaches including Cognitive Behavioral Therapy (CBT), Dialectical Behavior Therapy (DBT), Person Centered Therapy (PCT), and Reality Therapy (RT), each leading to different patterns of interpreting clients' mental states. LLMs without reasoning generated predominantly exploratory responses. However, when LLMs used CoE reasoning, we found a more comprehensive range of empathetic responses aligned with the different reasoning patterns of each psychotherapy model. The CBT based CoE resulted in the most balanced generation of empathetic responses. The findings underscore the importance of understanding the emotional context and how it affects human and AI communication. Our research contributes to understanding how psychotherapeutic models can be incorporated into LLMs, facilitating the development of context-specific, safer, and empathetic AI.
In the past several years, the convergence of the last iterate of the Stochastic Gradient Descent (SGD) algorithm has triggered people's interest due to its good performance in practice but lack of theoretical understanding. For Lipschitz and convex functions, different works have established the optimal $O(\log(1/\delta)\log T/\sqrt{T})$ or $O(\sqrt{\log(1/\delta)/T})$ high-probability convergence rates for the final iterate, where $T$ is the time horizon and $\delta$ is the failure probability. However, to prove these bounds, all the existing works are limited to compact domains or require almost surely bounded noises. It is natural to ask whether the last iterate of SGD can still guarantee the optimal convergence rate but without these two restrictive assumptions. Besides this important question, there are still lots of theoretical problems lacking an answer. For example, compared with the last iterate convergence of SGD for non-smooth problems, only few results for smooth optimization have yet been developed. Additionally, the existing results are all limited to a non-composite objective and the standard Euclidean norm. It still remains unclear whether the last-iterate convergence can be provably extended to wider composite optimization and non-Euclidean norms. In this work, to address the issues mentioned above, we revisit the last-iterate convergence of stochastic gradient methods and provide the first unified way to prove the convergence rates both in expectation and in high probability to accommodate general domains, composite objectives, non-Euclidean norms, Lipschitz conditions, smoothness and (strong) convexity simultaneously. Additionally, we extend our analysis to obtain the last-iterate convergence under heavy-tailed noises.
Diabetic Retinopathy (DR) is a prevalent illness associated with Diabetes which, if left untreated, can result in irreversible blindness. Deep Learning based systems are gradually being introduced as automated support for clinical diagnosis. Since healthcare has always been an extremely important domain demanding error-free performance, any adversaries could pose a big threat to the applicability of such systems. In this work, we use Universal Adversarial Perturbations (UAPs) to quantify the vulnerability of Medical Deep Neural Networks (DNNs) for detecting DR. To the best of our knowledge, this is the very first attempt that works on attacking complete fine-grained classification of DR images using various UAPs. Also, as a part of this work, we use UAPs to fine-tune the trained models to defend against adversarial samples. We experiment on several models and observe that the performance of such models towards unseen adversarial attacks gets boosted on average by $3.41$ Cohen-kappa value and maximum by $31.92$ Cohen-kappa value. The performance degradation on normal data upon ensembling the fine-tuned models was found to be statistically insignificant using t-test, highlighting the benefits of UAP-based adversarial fine-tuning.
Large Language Models (LLMs) have gained considerable traction within the Software Engineering (SE) community, impacting various SE tasks from code completion to test generation, from program repair to code summarization. Despite their promise, researchers must still be careful as numerous intricate factors can influence the outcomes of experiments involving LLMs. This paper initiates an open discussion on potential threats to the validity of LLM-based research including issues such as closed-source models, possible data leakage between LLM training data and research evaluation, and the reproducibility of LLM-based findings. In response, this paper proposes a set of guidelines tailored for SE researchers and Language Model (LM) providers to mitigate these concerns. The implications of the guidelines are illustrated using existing good practices followed by LLM providers and a practical example for SE researchers in the context of test case generation.
Thompson sampling (TS) has been known for its outstanding empirical performance supported by theoretical guarantees across various reward models in the classical stochastic multi-armed bandit problems. Nonetheless, its optimality is often restricted to specific priors due to the common observation that TS is fairly insensitive to the choice of the prior when it comes to asymptotic regret bounds. However, when the model contains multiple parameters, the optimality of TS highly depends on the choice of priors, which casts doubt on the generalizability of previous findings to other models. To address this gap, this study explores the impact of selecting noninformative priors, offering insights into the performance of TS when dealing with new models that lack theoretical understanding. We first extend the regret analysis of TS to the model of uniform distributions with unknown supports, which would be the simplest non-regular model. Our findings reveal that changing noninformative priors can significantly affect the expected regret, aligning with previously known results in other multiparameter bandit models. Although the uniform prior is shown to be optimal, we highlight the inherent limitation of its optimality, which is limited to specific parameterizations and emphasizes the significance of the invariance property of priors. In light of this limitation, we propose a slightly modified TS-based policy, called TS with Truncation (TS-T), which can achieve the asymptotic optimality for the Gaussian models and the uniform models by using the reference prior and the Jeffreys prior that are invariant under one-to-one reparameterizations. This policy provides an alternative approach to achieving optimality by employing fine-tuned truncation, which would be much easier than hunting for optimal priors in practice.
Knowledge Graph Embedding (KGE) aims to learn representations for entities and relations. Most KGE models have gained great success, especially on extrapolation scenarios. Specifically, given an unseen triple (h, r, t), a trained model can still correctly predict t from (h, r, ?), or h from (?, r, t), such extrapolation ability is impressive. However, most existing KGE works focus on the design of delicate triple modeling function, which mainly tells us how to measure the plausibility of observed triples, but offers limited explanation of why the methods can extrapolate to unseen data, and what are the important factors to help KGE extrapolate. Therefore in this work, we attempt to study the KGE extrapolation of two problems: 1. How does KGE extrapolate to unseen data? 2. How to design the KGE model with better extrapolation ability? For the problem 1, we first discuss the impact factors for extrapolation and from relation, entity and triple level respectively, propose three Semantic Evidences (SEs), which can be observed from train set and provide important semantic information for extrapolation. Then we verify the effectiveness of SEs through extensive experiments on several typical KGE methods. For the problem 2, to make better use of the three levels of SE, we propose a novel GNN-based KGE model, called Semantic Evidence aware Graph Neural Network (SE-GNN). In SE-GNN, each level of SE is modeled explicitly by the corresponding neighbor pattern, and merged sufficiently by the multi-layer aggregation, which contributes to obtaining more extrapolative knowledge representation. Finally, through extensive experiments on FB15k-237 and WN18RR datasets, we show that SE-GNN achieves state-of-the-art performance on Knowledge Graph Completion task and performs a better extrapolation ability.
Recently, Mutual Information (MI) has attracted attention in bounding the generalization error of Deep Neural Networks (DNNs). However, it is intractable to accurately estimate the MI in DNNs, thus most previous works have to relax the MI bound, which in turn weakens the information theoretic explanation for generalization. To address the limitation, this paper introduces a probabilistic representation of DNNs for accurately estimating the MI. Leveraging the proposed MI estimator, we validate the information theoretic explanation for generalization, and derive a tighter generalization bound than the state-of-the-art relaxations.
Graph Neural Networks (GNNs) have been studied from the lens of expressive power and generalization. However, their optimization properties are less well understood. We take the first step towards analyzing GNN training by studying the gradient dynamics of GNNs. First, we analyze linearized GNNs and prove that despite the non-convexity of training, convergence to a global minimum at a linear rate is guaranteed under mild assumptions that we validate on real-world graphs. Second, we study what may affect the GNNs' training speed. Our results show that the training of GNNs is implicitly accelerated by skip connections, more depth, and/or a good label distribution. Empirical results confirm that our theoretical results for linearized GNNs align with the training behavior of nonlinear GNNs. Our results provide the first theoretical support for the success of GNNs with skip connections in terms of optimization, and suggest that deep GNNs with skip connections would be promising in practice.
Graph Neural Networks (GNNs) have recently become increasingly popular due to their ability to learn complex systems of relations or interactions arising in a broad spectrum of problems ranging from biology and particle physics to social networks and recommendation systems. Despite the plethora of different models for deep learning on graphs, few approaches have been proposed thus far for dealing with graphs that present some sort of dynamic nature (e.g. evolving features or connectivity over time). In this paper, we present Temporal Graph Networks (TGNs), a generic, efficient framework for deep learning on dynamic graphs represented as sequences of timed events. Thanks to a novel combination of memory modules and graph-based operators, TGNs are able to significantly outperform previous approaches being at the same time more computationally efficient. We furthermore show that several previous models for learning on dynamic graphs can be cast as specific instances of our framework. We perform a detailed ablation study of different components of our framework and devise the best configuration that achieves state-of-the-art performance on several transductive and inductive prediction tasks for dynamic graphs.