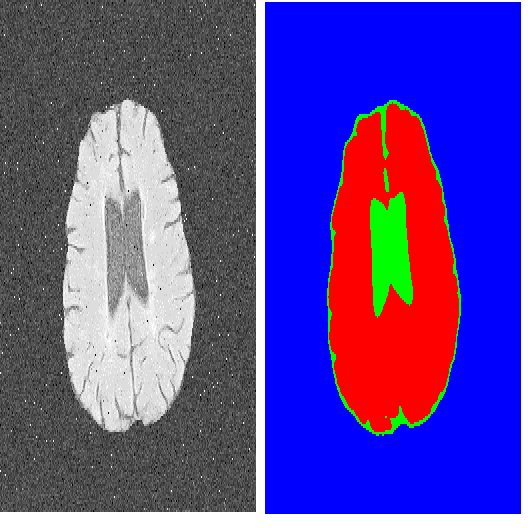
The minimal geodesic models based on the Eikonal equations are capable of finding suitable solutions in various image segmentation scenarios. Existing geodesic-based segmentation approaches usually exploit image features in conjunction with geometric regularization terms, such as Euclidean curve length or curvature-penalized length, for computing geodesic curves. In this paper, we take into account a more complicated problem: finding curvature-penalized geodesic paths with a convexity shape prior. We establish new geodesic models relying on the strategy of orientation-lifting, by which a planar curve can be mapped to an high-dimensional orientation-dependent space. The convexity shape prior serves as a constraint for the construction of local geodesic metrics encoding a particular curvature constraint. Then the geodesic distances and the corresponding closed geodesic paths in the orientation-lifted space can be efficiently computed through state-of-the-art Hamiltonian fast marching method. In addition, we apply the proposed geodesic models to the active contours, leading to efficient interactive image segmentation algorithms that preserve the advantages of convexity shape prior and curvature penalization.
相關內容
Standard neural networks struggle to generalize under distribution shifts in computer vision. Fortunately, combining multiple networks can consistently improve out-of-distribution generalization. In particular, weight averaging (WA) strategies were shown to perform best on the competitive DomainBed benchmark; they directly average the weights of multiple networks despite their nonlinearities. In this paper, we propose Diverse Weight Averaging (DiWA), a new WA strategy whose main motivation is to increase the functional diversity across averaged models. To this end, DiWA averages weights obtained from several independent training runs: indeed, models obtained from different runs are more diverse than those collected along a single run thanks to differences in hyperparameters and training procedures. We motivate the need for diversity by a new bias-variance-covariance-locality decomposition of the expected error, exploiting similarities between WA and standard functional ensembling. Moreover, this decomposition highlights that WA succeeds when the variance term dominates, which we show occurs when the marginal distribution changes at test time. Experimentally, DiWA consistently improves the state of the art on DomainBed without inference overhead.
As a framework for sequential decision-making, Reinforcement Learning (RL) has been regarded as an essential component leading to Artificial General Intelligence (AGI). However, RL is often criticized for having the same training environment as the test one, which also hinders its application in the real world. To mitigate this problem, Distributionally Robust RL (DRRL) is proposed to improve the worst performance in a set of environments that may contain the unknown test environment. Due to the nonlinearity of the robustness goal, most of the previous work resort to the model-based approach, learning with either an empirical distribution learned from the data or a simulator that can be sampled infinitely, which limits their applications in simple dynamics environments. In contrast, we attempt to design a DRRL algorithm that can be trained along a single trajectory, i.e., no repeated sampling from a state. Based on the standard Q-learning, we propose distributionally robust Q-learning with the single trajectory (DRQ) and its average-reward variant named differential DRQ. We provide asymptotic convergence guarantees and experiments for both settings, demonstrating their superiority in the perturbed environments against the non-robust ones.
As the size of the pre-trained language model (PLM) continues to increase, numerous parameter-efficient transfer learning methods have been proposed recently to compensate for the tremendous cost of fine-tuning. Despite the impressive results achieved by large pre-trained language models (PLMs) and various parameter-efficient transfer learning (PETL) methods on sundry benchmarks, it remains unclear if they can handle inputs that have been distributionally shifted effectively. In this study, we systematically explore how the ability to detect out-of-distribution (OOD) changes as the size of the PLM grows or the transfer methods are altered. Specifically, we evaluated various PETL techniques, including fine-tuning, Adapter, LoRA, and prefix-tuning, on three different intention classification tasks, each utilizing various language models with different scales.
We consider linear dynamical systems under floating-point rounding. In these systems, a matrix is repeatedly applied to a vector, but the numbers are rounded into floating-point representation after each step (i.e., stored as a fixed-precision mantissa and an exponent). The approach more faithfully models realistic implementations of linear loops, compared to the exact arbitrary-precision setting often employed in the study of linear dynamical systems. Our results are twofold: We show that for non-negative matrices there is a special structure to the sequence of vectors generated by the system: the mantissas are periodic and the exponents grow linearly. We leverage this to show decidability of $\omega$-regular temporal model checking against semialgebraic predicates. This contrasts with the unrounded setting, where even the non-negative case encompasses the long-standing open Skolem and Positivity problems. On the other hand, when negative numbers are allowed in the matrix, we show that the reachability problem is undecidable by encoding a two-counter machine. Again, this is in contrast with the unrounded setting where point-to-point reachability is known to be decidable in polynomial time.
Most of the literature on learning in games has focused on the restrictive setting where the underlying repeated game does not change over time. Much less is known about the convergence of no-regret learning algorithms in dynamic multiagent settings. In this paper, we characterize the convergence of \emph{optimistic gradient descent (OGD)} in time-varying games by drawing a strong connection with \emph{dynamic regret}. Our framework yields sharp convergence bounds for the equilibrium gap of OGD in zero-sum games parameterized on the \emph{minimal} first-order variation of the Nash equilibria and the second-order variation of the payoff matrices, subsuming known results for static games. Furthermore, we establish improved \emph{second-order} variation bounds under strong convexity-concavity, as long as each game is repeated multiple times. Our results also apply to time-varying \emph{general-sum} multi-player games via a bilinear formulation of correlated equilibria, which has novel implications for meta-learning and for obtaining refined variation-dependent regret bounds, addressing questions left open in prior papers. Finally, we leverage our framework to also provide new insights on dynamic regret guarantees in static games.
Limited look-ahead game solving for imperfect-information games is the breakthrough that allowed defeating expert humans in large poker. The existing algorithms of this type assume that all players are perfectly rational and do not allow explicit modeling and exploitation of the opponent's flaws. As a result, even very weak opponents can tie or lose only very slowly against these powerful methods. We present the first algorithm that allows incorporating opponent models into limited look-ahead game solving. Using only an approximation of a single (optimal) value function, the algorithm efficiently exploits an arbitrary estimate of the opponent's strategy. It guarantees a bounded worst-case loss for the player. We also show that using existing resolving gadgets is problematic and why we need to keep the previously solved parts of the game. Experiments on three different games show that over half of the maximum possible exploitation is achieved by our algorithm without risking almost any loss.
Graph neural networks (GNNs) achieve remarkable performance in graph machine learning tasks but can be hard to train on large-graph data, where their learning dynamics are not well understood. We investigate the training dynamics of large-graph GNNs using graph neural tangent kernels (GNTKs) and graphons. In the limit of large width, optimization of an overparametrized NN is equivalent to kernel regression on the NTK. Here, we investigate how the GNTK evolves as another independent dimension is varied: the graph size. We use graphons to define limit objects -- graphon NNs for GNNs, and graphon NTKs for GNTKs, and prove that, on a sequence of growing graphs, the GNTKs converge to the graphon NTK. We further prove that the eigenspaces of the GNTK, which are related to the problem learning directions and associated learning speeds, converge to the spectrum of the GNTK. This implies that in the large-graph limit, the GNTK fitted on a graph of moderate size can be used to solve the same task on the large-graph and infer the learning dynamics of the large-graph GNN. These results are verified empirically on node regression and node classification tasks.
To avoid poor empirical performance in Metropolis-Hastings and other accept-reject-based algorithms practitioners often tune them by trial and error. Lower bounds on the convergence rate are developed in both total variation and Wasserstein distances in order to identify how the simulations will fail so these settings can be avoided, providing guidance on tuning. Particular attention is paid to using the lower bounds to study the convergence complexity of accept-reject-based Markov chains and to constrain the rate of convergence for geometrically ergodic Markov chains. The theory is applied in several settings. For example, if the target density concentrates with a parameter $n$ (e.g. posterior concentration, Laplace approximations), it is demonstrated that the convergence rate of a Metropolis-Hastings chain can tend to $1$ exponentially fast if the tuning parameters do not depend carefully on $n$. This is demonstrated with Bayesian logistic regression with Zellner's g-prior when the dimension and sample increase in such a way that size $d/n \to \gamma \in (0, 1)$ and flat prior Bayesian logistic regression as $n \to \infty$.
While existing work in robust deep learning has focused on small pixel-level $\ell_p$ norm-based perturbations, this may not account for perturbations encountered in several real world settings. In many such cases although test data might not be available, broad specifications about the types of perturbations (such as an unknown degree of rotation) may be known. We consider a setup where robustness is expected over an unseen test domain that is not i.i.d. but deviates from the training domain. While this deviation may not be exactly known, its broad characterization is specified a priori, in terms of attributes. We propose an adversarial training approach which learns to generate new samples so as to maximize exposure of the classifier to the attributes-space, without having access to the data from the test domain. Our adversarial training solves a min-max optimization problem, with the inner maximization generating adversarial perturbations, and the outer minimization finding model parameters by optimizing the loss on adversarial perturbations generated from the inner maximization. We demonstrate the applicability of our approach on three types of naturally occurring perturbations -- object-related shifts, geometric transformations, and common image corruptions. Our approach enables deep neural networks to be robust against a wide range of naturally occurring perturbations. We demonstrate the usefulness of the proposed approach by showing the robustness gains of deep neural networks trained using our adversarial training on MNIST, CIFAR-10, and a new variant of the CLEVR dataset.
Retrieving object instances among cluttered scenes efficiently requires compact yet comprehensive regional image representations. Intuitively, object semantics can help build the index that focuses on the most relevant regions. However, due to the lack of bounding-box datasets for objects of interest among retrieval benchmarks, most recent work on regional representations has focused on either uniform or class-agnostic region selection. In this paper, we first fill the void by providing a new dataset of landmark bounding boxes, based on the Google Landmarks dataset, that includes $94k$ images with manually curated boxes from $15k$ unique landmarks. Then, we demonstrate how a trained landmark detector, using our new dataset, can be leveraged to index image regions and improve retrieval accuracy while being much more efficient than existing regional methods. In addition, we further introduce a novel regional aggregated selective match kernel (R-ASMK) to effectively combine information from detected regions into an improved holistic image representation. R-ASMK boosts image retrieval accuracy substantially at no additional memory cost, while even outperforming systems that index image regions independently. Our complete image retrieval system improves upon the previous state-of-the-art by significant margins on the Revisited Oxford and Paris datasets. Code and data will be released.