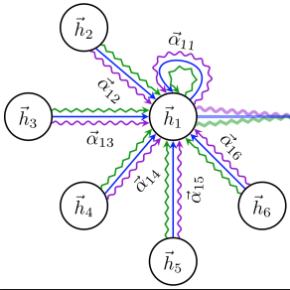
While the expressive power and computational capabilities of graph neural networks (GNNs) have been theoretically studied, their optimization and learning dynamics, in general, remain largely unexplored. Our study undertakes the Graph Attention Network (GAT), a popular GNN architecture in which a node's neighborhood aggregation is weighted by parameterized attention coefficients. We derive a conservation law of GAT gradient flow dynamics, which explains why a high portion of parameters in GATs with standard initialization struggle to change during training. This effect is amplified in deeper GATs, which perform significantly worse than their shallow counterparts. To alleviate this problem, we devise an initialization scheme that balances the GAT network. Our approach i) allows more effective propagation of gradients and in turn enables trainability of deeper networks, and ii) attains a considerable speedup in training and convergence time in comparison to the standard initialization. Our main theorem serves as a stepping stone to studying the learning dynamics of positive homogeneous models with attention mechanisms.
相關內容
The Segment Anything Model (SAM) is the first foundation model for general image segmentation. It has achieved impressive results on various natural image segmentation tasks. However, medical image segmentation (MIS) is more challenging because of the complex modalities, fine anatomical structures, uncertain and complex object boundaries, and wide-range object scales. To fully validate SAM's performance on medical data, we collected and sorted 53 open-source datasets and built a large medical segmentation dataset with 18 modalities, 84 objects, 125 object-modality paired targets, 1050K 2D images, and 6033K masks. We comprehensively analyzed different models and strategies on the so-called COSMOS 1050K dataset. Our findings mainly include the following: 1) SAM showed remarkable performance in some specific objects but was unstable, imperfect, or even totally failed in other situations. 2) SAM with the large ViT-H showed better overall performance than that with the small ViT-B. 3) SAM performed better with manual hints, especially box, than the Everything mode. 4) SAM could help human annotation with high labeling quality and less time. 5) SAM was sensitive to the randomness in the center point and tight box prompts, and may suffer from a serious performance drop. 6) SAM performed better than interactive methods with one or a few points, but will be outpaced as the number of points increases. 7) SAM's performance correlated to different factors, including boundary complexity, intensity differences, etc. 8) Finetuning the SAM on specific medical tasks could improve its average DICE performance by 4.39% and 6.68% for ViT-B and ViT-H, respectively. We hope that this comprehensive report can help researchers explore the potential of SAM applications in MIS, and guide how to appropriately use and develop SAM.
Channel knowledge map (CKM) has been recently proposed to enable environment-aware communications by utilizing historical or simulation generated wireless channel data. This paper studies the construction of one particular type of CKM, namely channel gain map (CGM), by using a finite number of measurements or simulation-generated data, with model-based spatial channel prediction. We try to answer the following question: How much data is sufficient for CKM construction? To this end, we first derive the average mean square error (AMSE) of the channel gain prediction as a function of the sample density of data collection for offline CGM construction, as well as the number of data points used for online spatial channel gain prediction. To model the spatial variation of the wireless environment even within each cell, we divide the CGM into subregions and estimate the channel parameters from the local data within each subregion. The parameter estimation error and the channel prediction error based on estimated channel parameters are derived as functions of the number of data points within the subregion. The analytical results provide useful guide for CGM construction and utilization by determining the required spatial sample density for offline data collection and number of data points to be used for online channel prediction, so that the desired level of channel prediction accuracy is guaranteed.
Transformers are a class of autoregressive deep learning architectures which have recently achieved state-of-the-art performance in various vision, language, and robotics tasks. We revisit the problem of Kalman Filtering in linear dynamical systems and show that Transformers can approximate the Kalman Filter in a strong sense. Specifically, for any observable LTI system we construct an explicit causally-masked Transformer which implements the Kalman Filter, up to a small additive error which is bounded uniformly in time; we call our construction the Transformer Filter. Our construction is based on a two-step reduction. We first show that a softmax self-attention block can exactly represent a certain Gaussian kernel smoothing estimator. We then show that this estimator closely approximates the Kalman Filter. We also investigate how the Transformer Filter can be used for measurement-feedback control and prove that the resulting nonlinear controllers closely approximate the performance of standard optimal control policies such as the LQG controller.
Since its introduction, the partial information decomposition (PID) has emerged as a powerful, information-theoretic technique useful for studying the structure of (potentially higher-order) interactions in complex systems. Despite its utility, the applicability of the PID is restricted by the need to assign elements as either inputs or targets, as well as the specific structure of the mutual information itself. Here, we introduce a generalized information decomposition that relaxes the source/target distinction while still satisfying the basic intuitions about information. This approach is based on the decomposition of the Kullback-Leibler divergence, and consequently allows for the analysis of any information gained when updating from an arbitrary prior to an arbitrary posterior. Consequently, any information-theoretic measure that can be written in as a Kullback-Leibler divergence admits a decomposition in the style of Williams and Beer, including the total correlation, the negentropy, and the mutual information as special cases. In this paper, we explore how the generalized information decomposition can reveal novel insights into existing measures, as well as the nature of higher-order synergies. We show that synergistic information is intimately related to the well-known Tononi-Sporns-Edelman (TSE) complexity, and that synergistic information requires a similar integration/segregation balance as a high TSE complexity. Finally, we end with a discussion of how this approach fits into other attempts to generalize the PID and the possibilities for empirical applications.
Feature attribution methods are popular in interpretable machine learning. These methods compute the attribution of each input feature to represent its importance, but there is no consensus on the definition of "attribution", leading to many competing methods with little systematic evaluation, complicated in particular by the lack of ground truth attribution. To address this, we propose a dataset modification procedure to induce such ground truth. Using this procedure, we evaluate three common methods: saliency maps, rationales, and attentions. We identify several deficiencies and add new perspectives to the growing body of evidence questioning the correctness and reliability of these methods applied on datasets in the wild. We further discuss possible avenues for remedy and recommend new attribution methods to be tested against ground truth before deployment. The code is available at \url{//github.com/YilunZhou/feature-attribution-evaluation}.
Residual networks (ResNets) have displayed impressive results in pattern recognition and, recently, have garnered considerable theoretical interest due to a perceived link with neural ordinary differential equations (neural ODEs). This link relies on the convergence of network weights to a smooth function as the number of layers increases. We investigate the properties of weights trained by stochastic gradient descent and their scaling with network depth through detailed numerical experiments. We observe the existence of scaling regimes markedly different from those assumed in neural ODE literature. Depending on certain features of the network architecture, such as the smoothness of the activation function, one may obtain an alternative ODE limit, a stochastic differential equation or neither of these. These findings cast doubts on the validity of the neural ODE model as an adequate asymptotic description of deep ResNets and point to an alternative class of differential equations as a better description of the deep network limit.
Non-convex optimization is ubiquitous in modern machine learning. Researchers devise non-convex objective functions and optimize them using off-the-shelf optimizers such as stochastic gradient descent and its variants, which leverage the local geometry and update iteratively. Even though solving non-convex functions is NP-hard in the worst case, the optimization quality in practice is often not an issue -- optimizers are largely believed to find approximate global minima. Researchers hypothesize a unified explanation for this intriguing phenomenon: most of the local minima of the practically-used objectives are approximately global minima. We rigorously formalize it for concrete instances of machine learning problems.
Graph Neural Networks (GNNs), which generalize deep neural networks to graph-structured data, have drawn considerable attention and achieved state-of-the-art performance in numerous graph related tasks. However, existing GNN models mainly focus on designing graph convolution operations. The graph pooling (or downsampling) operations, that play an important role in learning hierarchical representations, are usually overlooked. In this paper, we propose a novel graph pooling operator, called Hierarchical Graph Pooling with Structure Learning (HGP-SL), which can be integrated into various graph neural network architectures. HGP-SL incorporates graph pooling and structure learning into a unified module to generate hierarchical representations of graphs. More specifically, the graph pooling operation adaptively selects a subset of nodes to form an induced subgraph for the subsequent layers. To preserve the integrity of graph's topological information, we further introduce a structure learning mechanism to learn a refined graph structure for the pooled graph at each layer. By combining HGP-SL operator with graph neural networks, we perform graph level representation learning with focus on graph classification task. Experimental results on six widely used benchmarks demonstrate the effectiveness of our proposed model.
Graph Neural Networks (GNNs) for representation learning of graphs broadly follow a neighborhood aggregation framework, where the representation vector of a node is computed by recursively aggregating and transforming feature vectors of its neighboring nodes. Many GNN variants have been proposed and have achieved state-of-the-art results on both node and graph classification tasks. However, despite GNNs revolutionizing graph representation learning, there is limited understanding of their representational properties and limitations. Here, we present a theoretical framework for analyzing the expressive power of GNNs in capturing different graph structures. Our results characterize the discriminative power of popular GNN variants, such as Graph Convolutional Networks and GraphSAGE, and show that they cannot learn to distinguish certain simple graph structures. We then develop a simple architecture that is provably the most expressive among the class of GNNs and is as powerful as the Weisfeiler-Lehman graph isomorphism test. We empirically validate our theoretical findings on a number of graph classification benchmarks, and demonstrate that our model achieves state-of-the-art performance.
Recently, graph neural networks (GNNs) have revolutionized the field of graph representation learning through effectively learned node embeddings, and achieved state-of-the-art results in tasks such as node classification and link prediction. However, current GNN methods are inherently flat and do not learn hierarchical representations of graphs---a limitation that is especially problematic for the task of graph classification, where the goal is to predict the label associated with an entire graph. Here we propose DiffPool, a differentiable graph pooling module that can generate hierarchical representations of graphs and can be combined with various graph neural network architectures in an end-to-end fashion. DiffPool learns a differentiable soft cluster assignment for nodes at each layer of a deep GNN, mapping nodes to a set of clusters, which then form the coarsened input for the next GNN layer. Our experimental results show that combining existing GNN methods with DiffPool yields an average improvement of 5-10% accuracy on graph classification benchmarks, compared to all existing pooling approaches, achieving a new state-of-the-art on four out of five benchmark data sets.