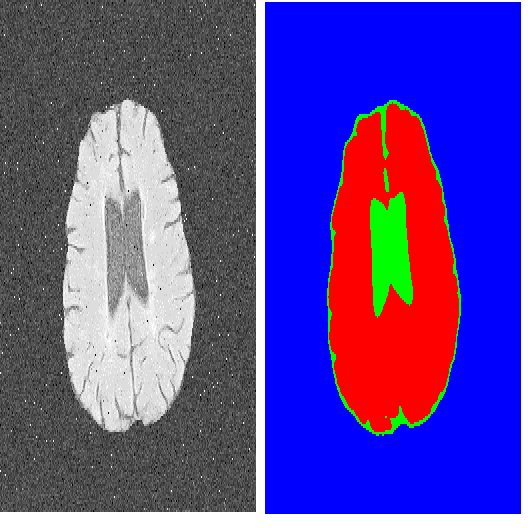
We develop confidence sets which provide spatial uncertainty guarantees for the output of a black-box machine learning model designed for image segmentation. To do so we adapt conformal inference to the imaging setting, obtaining thresholds on a calibration dataset based on the distribution of the maximum of the transformed logit scores within and outside of the ground truth masks. We prove that these confidence sets, when applied to new predictions of the model, are guaranteed to contain the true unknown segmented mask with desired probability. We show that learning appropriate score transformations on a learning dataset before performing calibration is crucial for optimizing performance. We illustrate and validate our approach on a polpys tumor dataset. To do so we obtain the logit scores from a deep neural network trained for polpys segmentation and show that using distance transformed scores to obtain outer confidence sets and the original scores for inner confidence sets enables tight bounds on tumor location whilst controlling the false coverage rate.
相關內容
We address the problem of identifying functional interactions among stochastic neurons with variable-length memory from their spiking activity. The neuronal network is modeled by a stochastic system of interacting point processes with variable-length memory. Each chain describes the activity of a single neuron, indicating whether it spikes at a given time. One neuron's influence on another can be either excitatory or inhibitory. To identify the existence and nature of an interaction between a neuron and its postsynaptic counterpart, we propose a model selection procedure based on the observation of the spike activity of a finite set of neurons over a finite time. The proposed procedure is also based on the maximum likelihood estimator for the synaptic weight matrix of the network neuronal model. In this sense, we prove the consistency of the maximum likelihood estimator followed by a proof of the consistency of the neighborhood interaction estimation procedure. The effectiveness of the proposed model selection procedure is demonstrated using simulated data, which validates the underlying theory. The method is also applied to analyze spike train data recorded from hippocampal neurons in rats during a visual attention task, where a computational model reconstructs the spiking activity and the results reveal interesting and biologically relevant information.
We perform a quantitative assessment of different strategies to compute the contribution due to surface tension in incompressible two-phase flows using a conservative level set (CLS) method. More specifically, we compare classical approaches, such as the direct computation of the curvature from the level set or the Laplace-Beltrami operator, with an evolution equation for the mean curvature recently proposed in literature. We consider the test case of a static bubble, for which an exact solution for the pressure jump across the interface is available, and the test case of an oscillating bubble, showing pros and cons of the different approaches.
We present BALDUR, a novel Bayesian algorithm designed to deal with multi-modal datasets and small sample sizes in high-dimensional settings while providing explainable solutions. To do so, the proposed model combines within a common latent space the different data views to extract the relevant information to solve the classification task and prune out the irrelevant/redundant features/data views. Furthermore, to provide generalizable solutions in small sample size scenarios, BALDUR efficiently integrates dual kernels over the views with a small sample-to-feature ratio. Finally, its linear nature ensures the explainability of the model outcomes, allowing its use for biomarker identification. This model was tested over two different neurodegeneration datasets, outperforming the state-of-the-art models and detecting features aligned with markers already described in the scientific literature.
Because of reinforcement learning's (RL) ability to automatically create more adaptive controlling logics beyond the hand-crafted heuristics, numerous effort has been made to apply RL to congestion control (CC) design for real time video communication (RTC) applications and has successfully shown promising benefits over the rule-based RTC CCs. Online reinforcement learning is often adopted to train the RL models so the models can directly adapt to real network environments. However, its trail-and-error manner can also cause catastrophic degradation of the quality of experience (QoE) of RTC application at run time. Thus, safeguard strategies such as falling back to hand-crafted heuristics can be used to run along with RL models to guarantee the actions explored in the training sensible, despite that these safeguard strategies interrupt the learning process and make it more challenging to discover optimal RL policies. The recent emergence of loss-tolerant neural video codecs (NVC) naturally provides a layer of protection for the online learning of RL-based congestion control because of its resilience to packet losses, but such packet loss resilience have not been fully exploited in prior works yet. In this paper, we present a reinforcement learning (RL) based congestion control which can be aware of and takes advantage of packet loss tolerance characteristic of NVCs via reward in online RL learning. Through extensive evaluation on various videos and network traces in a simulated environment, we demonstrate that our NVC-aware CC running with the loss-tolerant NVC reduces the training time by 41\% compared to other prior RL-based CCs. It also boosts the mean video quality by 0.3 to 1.6dB, lower the tail frame delay by 3 to 200ms, and reduces the video stalls by 20\% to 77\% in comparison with other baseline RTC CCs.
We study the numerical approximation of advection-diffusion equations with highly oscillatory coefficients and possibly dominant advection terms by means of the Multiscale Finite Element Method. The latter method is a now classical, finite element type method that performs a Galerkin approximation on a problem-dependent basis set, itself pre-computed in an offline stage. The approach is implemented here using basis functions that locally resolve both the diffusion and the advection terms. Variants with additional bubble functions and possibly weak inter-element continuity are proposed. Some theoretical arguments and a comprehensive set of numerical experiments allow to investigate and compare the stability and the accuracy of the approaches. The best approach constructed is shown to be adequate for both the diffusion- and advection-dominated regimes, and does not rely on an auxiliary stabilization parameter that would have to be properly adjusted.
Models implicitly defined through a random simulator of a process have become widely used in scientific and industrial applications in recent years. However, simulation-based inference methods for such implicit models, like approximate Bayesian computation (ABC), often scale poorly as data size increases. We develop a scalable inference method for implicitly defined models using a metamodel for the Monte Carlo log-likelihood estimator derived from simulations. This metamodel characterizes both statistical and simulation-based randomness in the distribution of the log-likelihood estimator across different parameter values. Our metamodel-based method quantifies uncertainty in parameter estimation in a principled manner, leveraging the local asymptotic normality of the mean function of the log-likelihood estimator. We apply this method to construct accurate confidence intervals for parameters of partially observed Markov process models where the Monte Carlo log-likelihood estimator is obtained using the bootstrap particle filter. We numerically demonstrate that our method enables accurate and highly scalable parameter inference across several examples, including a mechanistic compartment model for infectious diseases.
This short note introduces a novel diagnostic tool for evaluating the convection boundedness properties of numerical schemes across discontinuities. The proposed method is based on the convection boundedness criterion and the normalised variable diagram. By utilising this tool, we can determine the CFL conditions for numerical schemes to satisfy the convection boundedness criterion, identify the locations of over- and under-shoots, optimize the free parameters in the schemes, and develop strategies to prevent numerical oscillations across the discontinuity. We apply the diagnostic tool to assess representative discontinuity-capturing schemes, including THINC, fifth-order WENO, and fifth-order TENO, and validate the conclusions drawn through numerical tests. We further demonstrate the application of the proposed method by formulating a new THINC scheme with less stringent CFL conditions.
We first present a simple recursive algorithm that generates cyclic rotation Gray codes for stamp foldings and semi-meanders, where consecutive strings differ by a stamp rotation. These are the first known Gray codes for stamp foldings and semi-meanders, and we thus solve an open problem posted by Sawada and Li in [Electron. J. Comb. 19(2), 2012]. We then introduce an iterative algorithm that generates the same rotation Gray codes for stamp foldings and semi-meanders. Both the recursive and iterative algorithms generate stamp foldings and semi-meanders in constant amortized time and $O(n)$-amortized time per string respectively, using a linear amount of memory.
We explore the theoretical possibility of learning $d$-dimensional targets with $W$-parameter models by gradient flow (GF) when $W<d$. Our main result shows that if the targets are described by a particular $d$-dimensional probability distribution, then there exist models with as few as two parameters that can learn the targets with arbitrarily high success probability. On the other hand, we show that for $W<d$ there is necessarily a large subset of GF-non-learnable targets. In particular, the set of learnable targets is not dense in $\mathbb R^d$, and any subset of $\mathbb R^d$ homeomorphic to the $W$-dimensional sphere contains non-learnable targets. Finally, we observe that the model in our main theorem on almost guaranteed two-parameter learning is constructed using a hierarchical procedure and as a result is not expressible by a single elementary function. We show that this limitation is essential in the sense that most models written in terms of elementary functions cannot achieve the learnability demonstrated in this theorem.
We propose a simple methodology to approximate functions with given asymptotic behavior by specifically constructed terms and an unconstrained deep neural network (DNN). The methodology we describe extends to various asymptotic behaviors and multiple dimensions and is easy to implement. In this work we demonstrate it for linear asymptotic behavior in one-dimensional examples. We apply it to function approximation and regression problems where we measure approximation of only function values (``Vanilla Machine Learning''-VML) or also approximation of function and derivative values (``Differential Machine Learning''-DML) on several examples. We see that enforcing given asymptotic behavior leads to better approximation and faster convergence.