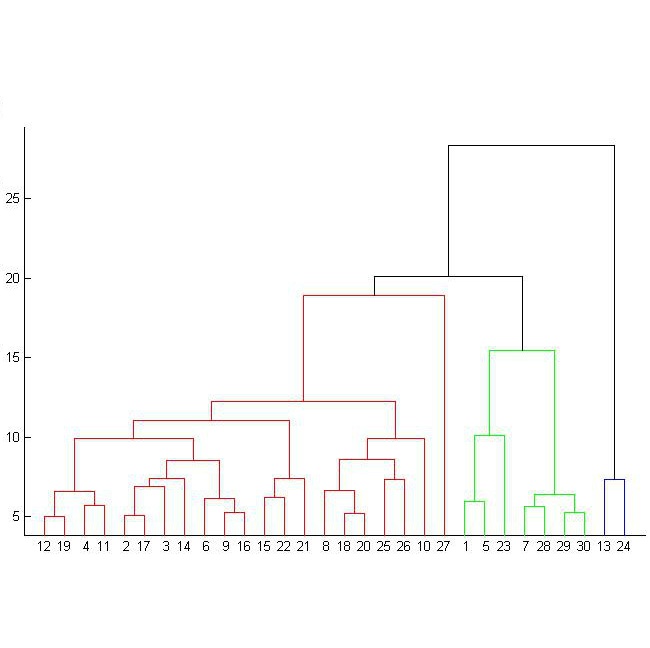
In collaborative learning, multiple parties contribute their datasets to jointly deduce global machine learning models for numerous predictive tasks. Despite its efficacy, this learning paradigm fails to encompass critical application domains that involve highly sensitive data, such as healthcare and security analytics, where privacy risks limit entities to individually train models using only their own datasets. In this work, we target privacy-preserving collaborative hierarchical clustering. We introduce a formal security definition that aims to achieve the balance between utility and privacy and present a two-party protocol that provably satisfies it. We then extend our protocol with: (i) an optimized version for the single-linkage clustering, and (ii) scalable approximation variants. We implement all our schemes and experimentally evaluate their performance and accuracy on synthetic and real datasets, obtaining very encouraging results. For example, end-to-end execution of our secure approximate protocol for over 1M 10-dimensional data samples requires 35sec of computation and achieves 97.09% accuracy.
相關內容
In statistical learning and analysis from shared data, which is increasingly widely adopted in platforms such as federated learning and meta-learning, there are two major concerns: privacy and robustness. Each participating individual should be able to contribute without the fear of leaking one's sensitive information. At the same time, the system should be robust in the presence of malicious participants inserting corrupted data. Recent algorithmic advances in learning from shared data focus on either one of these threats, leaving the system vulnerable to the other. We bridge this gap for the canonical problem of estimating the mean from i.i.d. samples. We introduce PRIME, which is the first efficient algorithm that achieves both privacy and robustness for a wide range of distributions. We further complement this result with a novel exponential time algorithm that improves the sample complexity of PRIME, achieving a near-optimal guarantee and matching a known lower bound for (non-robust) private mean estimation. This proves that there is no extra statistical cost to simultaneously guaranteeing privacy and robustness.
The structure of many complex networks includes edge directionality and weights on top of their topology. Network analysis that can seamlessly consider combination of these properties are desirable. In this paper, we study two important such network analysis techniques, namely, centrality and clustering. An information-flow based model is adopted for clustering, which itself builds upon an information theoretic measure for computing centrality. Our principal contributions include a generalized model of Markov entropic centrality with the flexibility to tune the importance of node degrees, edge weights and directions, with a closed-form asymptotic analysis. It leads to a novel two-stage graph clustering algorithm. The centrality analysis helps reason about the suitability of our approach to cluster a given graph, and determine `query' nodes, around which to explore local community structures, leading to an agglomerative clustering mechanism. The entropic centrality computations are amortized by our clustering algorithm, making it computationally efficient: compared to prior approaches using Markov entropic centrality for clustering, our experiments demonstrate multiple orders of magnitude of speed-up. Our clustering algorithm naturally inherits the flexibility to accommodate edge directionality, as well as different interpretations and interplay between edge weights and node degrees. Overall, this paper thus not only makes significant theoretical and conceptual contributions, but also translates the findings into artifacts of practical relevance, yielding new, effective and scalable centrality computations and graph clustering algorithms, whose efficacy has been validated through extensive benchmarking experiments.
This paper studies the hierarchical clustering problem, where the goal is to produce a dendrogram that represents clusters at varying scales of a data set. We propose the ParChain framework for designing parallel hierarchical agglomerative clustering (HAC) algorithms, and using the framework we obtain novel parallel algorithms for the complete linkage, average linkage, and Ward's linkage criteria. Compared to most previous parallel HAC algorithms, which require quadratic memory, our new algorithms require only linear memory, and are scalable to large data sets. ParChain is based on our parallelization of the nearest-neighbor chain algorithm, and enables multiple clusters to be merged on every round. We introduce two key optimizations that are critical for efficiency: a range query optimization that reduces the number of distance computations required when finding nearest neighbors of clusters, and a caching optimization that stores a subset of previously computed distances, which are likely to be reused. Experimentally, we show that our highly-optimized implementations using 48 cores with two-way hyper-threading achieve 5.8--110.1x speedup over state-of-the-art parallel HAC algorithms and achieve 13.75--54.23x self-relative speedup. Compared to state-of-the-art algorithms, our algorithms require up to 237.3x less space. Our algorithms are able to scale to data set sizes with tens of millions of points, which existing algorithms are not able to handle.
Anomaly and outlier detection is a long-standing problem in machine learning. In some cases, anomaly detection is easy, such as when data are drawn from well-characterized distributions such as the Gaussian. However, when data occupy high-dimensional spaces, anomaly detection becomes more difficult. We present CLAM (Clustered Learning of Approximate Manifolds), a manifold mapping technique in any metric space. CLAM begins with a fast hierarchical clustering technique and then induces a graph from the cluster tree, based on overlapping clusters as selected using several geometric and topological features. Using these graphs, we implement CHAODA (Clustered Hierarchical Anomaly and Outlier Detection Algorithms), exploring various properties of the graphs and their constituent clusters to find outliers. CHAODA employs a form of transfer learning based on a training set of datasets, and applies this knowledge to a separate test set of datasets of different cardinalities, dimensionalities, and domains. On 24 publicly available datasets, we compare CHAODA (by measure of ROC AUC) to a variety of state-of-the-art unsupervised anomaly-detection algorithms. Six of the datasets are used for training. CHAODA outperforms other approaches on 16 of the remaining 18 datasets. CLAM and CHAODA scale to large, high-dimensional "big data" anomaly-detection problems, and generalize across datasets and distance functions. Source code to CLAM and CHAODA are freely available on GitHub at //github.com/URI-ABD/clam.
Contextual multi-armed bandit (MAB) achieves cutting-edge performance on a variety of problems. When it comes to real-world scenarios such as recommendation system and online advertising, however, it is essential to consider the resource consumption of exploration. In practice, there is typically non-zero cost associated with executing a recommendation (arm) in the environment, and hence, the policy should be learned with a fixed exploration cost constraint. It is challenging to learn a global optimal policy directly, since it is a NP-hard problem and significantly complicates the exploration and exploitation trade-off of bandit algorithms. Existing approaches focus on solving the problems by adopting the greedy policy which estimates the expected rewards and costs and uses a greedy selection based on each arm's expected reward/cost ratio using historical observation until the exploration resource is exhausted. However, existing methods are hard to extend to infinite time horizon, since the learning process will be terminated when there is no more resource. In this paper, we propose a hierarchical adaptive contextual bandit method (HATCH) to conduct the policy learning of contextual bandits with a budget constraint. HATCH adopts an adaptive method to allocate the exploration resource based on the remaining resource/time and the estimation of reward distribution among different user contexts. In addition, we utilize full of contextual feature information to find the best personalized recommendation. Finally, in order to prove the theoretical guarantee, we present a regret bound analysis and prove that HATCH achieves a regret bound as low as $O(\sqrt{T})$. The experimental results demonstrate the effectiveness and efficiency of the proposed method on both synthetic data sets and the real-world applications.
Alternating Direction Method of Multipliers (ADMM) is a widely used tool for machine learning in distributed settings, where a machine learning model is trained over distributed data sources through an interactive process of local computation and message passing. Such an iterative process could cause privacy concerns of data owners. The goal of this paper is to provide differential privacy for ADMM-based distributed machine learning. Prior approaches on differentially private ADMM exhibit low utility under high privacy guarantee and often assume the objective functions of the learning problems to be smooth and strongly convex. To address these concerns, we propose a novel differentially private ADMM-based distributed learning algorithm called DP-ADMM, which combines an approximate augmented Lagrangian function with time-varying Gaussian noise addition in the iterative process to achieve higher utility for general objective functions under the same differential privacy guarantee. We also apply the moments accountant method to bound the end-to-end privacy loss. The theoretical analysis shows that DP-ADMM can be applied to a wider class of distributed learning problems, is provably convergent, and offers an explicit utility-privacy tradeoff. To our knowledge, this is the first paper to provide explicit convergence and utility properties for differentially private ADMM-based distributed learning algorithms. The evaluation results demonstrate that our approach can achieve good convergence and model accuracy under high end-to-end differential privacy guarantee.
We present a new clustering method in the form of a single clustering equation that is able to directly discover groupings in the data. The main proposition is that the first neighbor of each sample is all one needs to discover large chains and finding the groups in the data. In contrast to most existing clustering algorithms our method does not require any hyper-parameters, distance thresholds and/or the need to specify the number of clusters. The proposed algorithm belongs to the family of hierarchical agglomerative methods. The technique has a very low computational overhead, is easily scalable and applicable to large practical problems. Evaluation on well known datasets from different domains ranging between 1077 and 8.1 million samples shows substantial performance gains when compared to the existing clustering techniques.
The availability of large microarray data has led to a growing interest in biclustering methods in the past decade. Several algorithms have been proposed to identify subsets of genes and conditions according to different similarity measures and under varying constraints. In this paper we focus on the exclusive row biclustering problem for gene expression data sets, in which each row can only be a member of a single bicluster while columns can participate in multiple ones. This type of biclustering may be adequate, for example, for clustering groups of cancer patients where each patient (row) is expected to be carrying only a single type of cancer, while each cancer type is associated with multiple (and possibly overlapping) genes (columns). We present a novel method to identify these exclusive row biclusters through a combination of existing biclustering algorithms and combinatorial auction techniques. We devise an approach for tuning the threshold for our algorithm based on comparison to a null model in the spirit of the Gap statistic approach. We demonstrate our approach on both synthetic and real-world gene expression data and show its power in identifying large span non-overlapping rows sub matrices, while considering their unique nature. The Gap statistic approach succeeds in identifying appropriate thresholds in all our examples.
Machine Learning is a widely-used method for prediction generation. These predictions are more accurate when the model is trained on a larger dataset. On the other hand, the data is usually divided amongst different entities. For privacy reasons, the training can be done locally and then the model can be safely aggregated amongst the participants. However, if there are only two participants in \textit{Collaborative Learning}, the safe aggregation loses its power since the output of the training already contains much information about the participants. To resolve this issue, they must employ privacy-preserving mechanisms, which inevitably affect the accuracy of the model. In this paper, we model the training process as a two-player game where each player aims to achieve a higher accuracy while preserving its privacy. We introduce the notion of \textit{Price of Privacy}, a novel approach to measure the effect of privacy protection on the accuracy of the model. We develop a theoretical model for different player types, and we either find or prove the existence of a Nash Equilibrium with some assumptions. Moreover, we confirm these assumptions via a Recommendation Systems use case: for a specific learning algorithm, we apply three privacy-preserving mechanisms on two real-world datasets. Finally, as a complementary work for the designed game, we interpolate the relationship between privacy and accuracy for this use case and present three other methods to approximate it in a real-world scenario.
We develop an approach to risk minimization and stochastic optimization that provides a convex surrogate for variance, allowing near-optimal and computationally efficient trading between approximation and estimation error. Our approach builds off of techniques for distributionally robust optimization and Owen's empirical likelihood, and we provide a number of finite-sample and asymptotic results characterizing the theoretical performance of the estimator. In particular, we show that our procedure comes with certificates of optimality, achieving (in some scenarios) faster rates of convergence than empirical risk minimization by virtue of automatically balancing bias and variance. We give corroborating empirical evidence showing that in practice, the estimator indeed trades between variance and absolute performance on a training sample, improving out-of-sample (test) performance over standard empirical risk minimization for a number of classification problems.