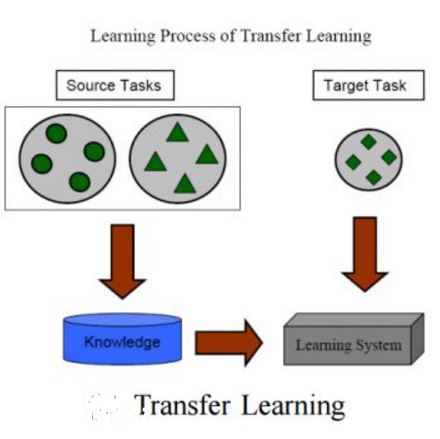
We study the generalization behavior of transfer learning of deep neural networks (DNNs). We adopt the overparameterization perspective -- featuring interpolation of the training data (i.e., approximately zero train error) and the double descent phenomenon -- to explain the delicate effect of the transfer learning setting on generalization performance. We study how the generalization behavior of transfer learning is affected by the dataset size in the source and target tasks, the number of transferred layers that are kept frozen in the target DNN training, and the similarity between the source and target tasks. We show that the test error evolution during the target DNN training has a more significant double descent effect when the target training dataset is sufficiently large. In addition, a larger source training dataset can yield a slower target DNN training. Moreover, we demonstrate that the number of frozen layers can determine whether the transfer learning is effectively underparameterized or overparameterized and, in turn, this may induce a freezing-wise double descent phenomenon that determines the relative success or failure of learning. Also, we show that the double descent phenomenon may make a transfer from a less related source task better than a transfer from a more related source task. We establish our results using image classification experiments with the ResNet, DenseNet and the vision transformer (ViT) architectures.
相關內容
Going beyond stochastic gradient descent (SGD), what new phenomena emerge in wide neural networks trained by adaptive optimizers like Adam? Here we show: The same dichotomy between feature learning and kernel behaviors (as in SGD) holds for general optimizers as well, including Adam -- albeit with a nonlinear notion of "kernel." We derive the corresponding "neural tangent" and "maximal update" limits for any architecture. Two foundational advances underlie the above results: 1) A new Tensor Program language, NEXORT, that can express how adaptive optimizers process gradients into updates. 2) The introduction of bra-ket notation to drastically simplify expressions and calculations in Tensor Programs. This work summarizes and generalizes all previous results in the Tensor Programs series of papers.
Graph neural networks (GNNs), as the de-facto model class for representation learning on graphs, are built upon the multi-layer perceptrons (MLP) architecture with additional message passing layers to allow features to flow across nodes. While conventional wisdom commonly attributes the success of GNNs to their advanced expressivity, we conjecture that this is not the main cause of GNNs' superiority in node-level prediction tasks. This paper pinpoints the major source of GNNs' performance gain to their intrinsic generalization capability, by introducing an intermediate model class dubbed as P(ropagational)MLP, which is identical to standard MLP in training, but then adopts GNN's architecture in testing. Intriguingly, we observe that PMLPs consistently perform on par with (or even exceed) their GNN counterparts, while being much more efficient in training. This finding sheds new insights into understanding the learning behavior of GNNs, and can be used as an analytic tool for dissecting various GNN-related research problems. As an initial step to analyze the inherent generalizability of GNNs, we show the essential difference between MLP and PMLP at infinite-width limit lies in the NTK feature map in the post-training stage. Moreover, by examining their extrapolation behavior, we find that though many GNNs and their PMLP counterparts cannot extrapolate non-linear functions for extremely out-of-distribution samples, they have greater potential to generalize to testing samples near the training data range as natural advantages of GNN architectures.
Causal inference plays a vital role in diverse domains like epidemiology, healthcare, and economics. De-confounding and counterfactual prediction in observational data has emerged as a prominent concern in causal inference research. While existing models tackle observed confounders, the presence of unobserved confounders remains a significant challenge, distorting causal inference and impacting counterfactual outcome accuracy. To address this, we propose a novel variational learning model of unobserved confounders for counterfactual inference (VLUCI), which generates the posterior distribution of unobserved confounders. VLUCI relaxes the unconfoundedness assumption often overlooked by most causal inference methods. By disentangling observed and unobserved confounders, VLUCI constructs a doubly variational inference model to approximate the distribution of unobserved confounders, which are used for inferring more accurate counterfactual outcomes. Extensive experiments on synthetic and semi-synthetic datasets demonstrate VLUCI's superior performance in inferring unobserved confounders. It is compatible with state-of-the-art counterfactual inference models, significantly improving inference accuracy at both group and individual levels. Additionally, VLUCI provides confidence intervals for counterfactual outcomes, aiding decision-making in risk-sensitive domains. We further clarify the considerations when applying VLUCI to cases where unobserved confounders don't strictly conform to our model assumptions using the public IHDP dataset as an example, highlighting the practical advantages of VLUCI.
Multimodality Representation Learning, as a technique of learning to embed information from different modalities and their correlations, has achieved remarkable success on a variety of applications, such as Visual Question Answering (VQA), Natural Language for Visual Reasoning (NLVR), and Vision Language Retrieval (VLR). Among these applications, cross-modal interaction and complementary information from different modalities are crucial for advanced models to perform any multimodal task, e.g., understand, recognize, retrieve, or generate optimally. Researchers have proposed diverse methods to address these tasks. The different variants of transformer-based architectures performed extraordinarily on multiple modalities. This survey presents the comprehensive literature on the evolution and enhancement of deep learning multimodal architectures to deal with textual, visual and audio features for diverse cross-modal and modern multimodal tasks. This study summarizes the (i) recent task-specific deep learning methodologies, (ii) the pretraining types and multimodal pretraining objectives, (iii) from state-of-the-art pretrained multimodal approaches to unifying architectures, and (iv) multimodal task categories and possible future improvements that can be devised for better multimodal learning. Moreover, we prepare a dataset section for new researchers that covers most of the benchmarks for pretraining and finetuning. Finally, major challenges, gaps, and potential research topics are explored. A constantly-updated paperlist related to our survey is maintained at //github.com/marslanm/multimodality-representation-learning.
Graph neural networks generalize conventional neural networks to graph-structured data and have received widespread attention due to their impressive representation ability. In spite of the remarkable achievements, the performance of Euclidean models in graph-related learning is still bounded and limited by the representation ability of Euclidean geometry, especially for datasets with highly non-Euclidean latent anatomy. Recently, hyperbolic space has gained increasing popularity in processing graph data with tree-like structure and power-law distribution, owing to its exponential growth property. In this survey, we comprehensively revisit the technical details of the current hyperbolic graph neural networks, unifying them into a general framework and summarizing the variants of each component. More importantly, we present various HGNN-related applications. Last, we also identify several challenges, which potentially serve as guidelines for further flourishing the achievements of graph learning in hyperbolic spaces.
In light of the emergence of deep reinforcement learning (DRL) in recommender systems research and several fruitful results in recent years, this survey aims to provide a timely and comprehensive overview of the recent trends of deep reinforcement learning in recommender systems. We start with the motivation of applying DRL in recommender systems. Then, we provide a taxonomy of current DRL-based recommender systems and a summary of existing methods. We discuss emerging topics and open issues, and provide our perspective on advancing the domain. This survey serves as introductory material for readers from academia and industry into the topic and identifies notable opportunities for further research.
Normalization is known to help the optimization of deep neural networks. Curiously, different architectures require specialized normalization methods. In this paper, we study what normalization is effective for Graph Neural Networks (GNNs). First, we adapt and evaluate the existing methods from other domains to GNNs. Faster convergence is achieved with InstanceNorm compared to BatchNorm and LayerNorm. We provide an explanation by showing that InstanceNorm serves as a preconditioner for GNNs, but such preconditioning effect is weaker with BatchNorm due to the heavy batch noise in graph datasets. Second, we show that the shift operation in InstanceNorm results in an expressiveness degradation of GNNs for highly regular graphs. We address this issue by proposing GraphNorm with a learnable shift. Empirically, GNNs with GraphNorm converge faster compared to GNNs using other normalization. GraphNorm also improves the generalization of GNNs, achieving better performance on graph classification benchmarks.
Deep neural networks (DNNs) are successful in many computer vision tasks. However, the most accurate DNNs require millions of parameters and operations, making them energy, computation and memory intensive. This impedes the deployment of large DNNs in low-power devices with limited compute resources. Recent research improves DNN models by reducing the memory requirement, energy consumption, and number of operations without significantly decreasing the accuracy. This paper surveys the progress of low-power deep learning and computer vision, specifically in regards to inference, and discusses the methods for compacting and accelerating DNN models. The techniques can be divided into four major categories: (1) parameter quantization and pruning, (2) compressed convolutional filters and matrix factorization, (3) network architecture search, and (4) knowledge distillation. We analyze the accuracy, advantages, disadvantages, and potential solutions to the problems with the techniques in each category. We also discuss new evaluation metrics as a guideline for future research.
Small data challenges have emerged in many learning problems, since the success of deep neural networks often relies on the availability of a huge amount of labeled data that is expensive to collect. To address it, many efforts have been made on training complex models with small data in an unsupervised and semi-supervised fashion. In this paper, we will review the recent progresses on these two major categories of methods. A wide spectrum of small data models will be categorized in a big picture, where we will show how they interplay with each other to motivate explorations of new ideas. We will review the criteria of learning the transformation equivariant, disentangled, self-supervised and semi-supervised representations, which underpin the foundations of recent developments. Many instantiations of unsupervised and semi-supervised generative models have been developed on the basis of these criteria, greatly expanding the territory of existing autoencoders, generative adversarial nets (GANs) and other deep networks by exploring the distribution of unlabeled data for more powerful representations. While we focus on the unsupervised and semi-supervised methods, we will also provide a broader review of other emerging topics, from unsupervised and semi-supervised domain adaptation to the fundamental roles of transformation equivariance and invariance in training a wide spectrum of deep networks. It is impossible for us to write an exclusive encyclopedia to include all related works. Instead, we aim at exploring the main ideas, principles and methods in this area to reveal where we are heading on the journey towards addressing the small data challenges in this big data era.
With the advent of deep neural networks, learning-based approaches for 3D reconstruction have gained popularity. However, unlike for images, in 3D there is no canonical representation which is both computationally and memory efficient yet allows for representing high-resolution geometry of arbitrary topology. Many of the state-of-the-art learning-based 3D reconstruction approaches can hence only represent very coarse 3D geometry or are limited to a restricted domain. In this paper, we propose occupancy networks, a new representation for learning-based 3D reconstruction methods. Occupancy networks implicitly represent the 3D surface as the continuous decision boundary of a deep neural network classifier. In contrast to existing approaches, our representation encodes a description of the 3D output at infinite resolution without excessive memory footprint. We validate that our representation can efficiently encode 3D structure and can be inferred from various kinds of input. Our experiments demonstrate competitive results, both qualitatively and quantitatively, for the challenging tasks of 3D reconstruction from single images, noisy point clouds and coarse discrete voxel grids. We believe that occupancy networks will become a useful tool in a wide variety of learning-based 3D tasks.