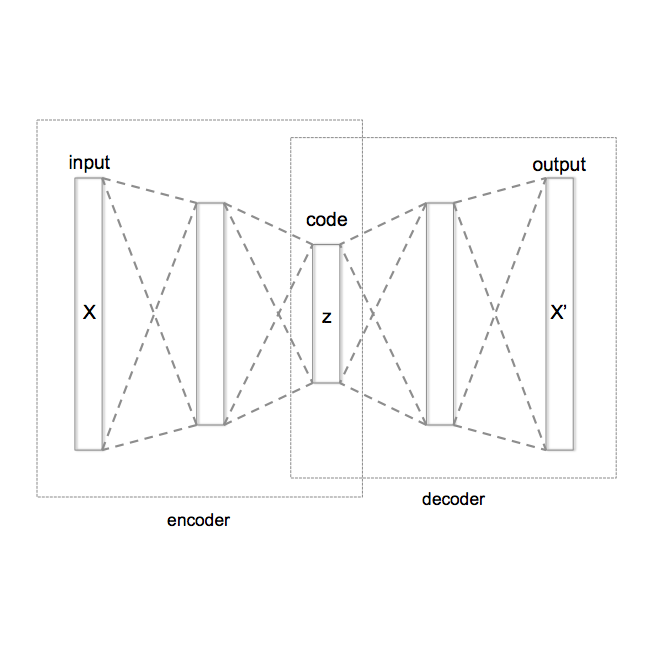
Variational autoencoders (VAEs) are influential generative models with rich representation capabilities from the deep neural network architecture and Bayesian method. However, VAE models have a weakness that assign a higher likelihood to out-of-distribution (OOD) inputs than in-distribution (ID) inputs. To address this problem, a reliable uncertainty estimation is considered to be critical for in-depth understanding of OOD inputs. In this study, we propose an improved noise contrastive prior (INCP) to be able to integrate into the encoder of VAEs, called INCPVAE. INCP is scalable, trainable and compatible with VAEs, and it also adopts the merits from the INCP for uncertainty estimation. Experiments on various datasets demonstrate that compared to the standard VAEs, our model is superior in uncertainty estimation for the OOD data and is robust in anomaly detection tasks. The INCPVAE model obtains reliable uncertainty estimation for OOD inputs and solves the OOD problem in VAE models.
相關內容
Transformers are state-of-the-art in a wide range of NLP tasks and have also been applied to many real-world products. Understanding the reliability and certainty of transformer model predictions is crucial for building trustable machine learning applications, e.g., medical diagnosis. Although many recent transformer extensions have been proposed, the study of the uncertainty estimation of transformer models is under-explored. In this work, we propose a novel way to enable transformers to have the capability of uncertainty estimation and, meanwhile, retain the original predictive performance. This is achieved by learning a hierarchical stochastic self-attention that attends to values and a set of learnable centroids, respectively. Then new attention heads are formed with a mixture of sampled centroids using the Gumbel-Softmax trick. We theoretically show that the self-attention approximation by sampling from a Gumbel distribution is upper bounded. We empirically evaluate our model on two text classification tasks with both in-domain (ID) and out-of-domain (OOD) datasets. The experimental results demonstrate that our approach: (1) achieves the best predictive performance and uncertainty trade-off among compared methods; (2) exhibits very competitive (in most cases, improved) predictive performance on ID datasets; (3) is on par with Monte Carlo dropout and ensemble methods in uncertainty estimation on OOD datasets.
Classic machine learning methods are built on the $i.i.d.$ assumption that training and testing data are independent and identically distributed. However, in real scenarios, the $i.i.d.$ assumption can hardly be satisfied, rendering the sharp drop of classic machine learning algorithms' performances under distributional shifts, which indicates the significance of investigating the Out-of-Distribution generalization problem. Out-of-Distribution (OOD) generalization problem addresses the challenging setting where the testing distribution is unknown and different from the training. This paper serves as the first effort to systematically and comprehensively discuss the OOD generalization problem, from the definition, methodology, evaluation to the implications and future directions. Firstly, we provide the formal definition of the OOD generalization problem. Secondly, existing methods are categorized into three parts based on their positions in the whole learning pipeline, namely unsupervised representation learning, supervised model learning and optimization, and typical methods for each category are discussed in detail. We then demonstrate the theoretical connections of different categories, and introduce the commonly used datasets and evaluation metrics. Finally, we summarize the whole literature and raise some future directions for OOD generalization problem. The summary of OOD generalization methods reviewed in this survey can be found at //out-of-distribution-generalization.com.
Deep neural networks have significantly contributed to the success in predictive accuracy for classification tasks. However, they tend to make over-confident predictions in real-world settings, where domain shifting and out-of-distribution (OOD) examples exist. Most research on uncertainty estimation focuses on computer vision because it provides visual validation on uncertainty quality. However, few have been presented in the natural language process domain. Unlike Bayesian methods that indirectly infer uncertainty through weight uncertainties, current evidential uncertainty-based methods explicitly model the uncertainty of class probabilities through subjective opinions. They further consider inherent uncertainty in data with different root causes, vacuity (i.e., uncertainty due to a lack of evidence) and dissonance (i.e., uncertainty due to conflicting evidence). In our paper, we firstly apply evidential uncertainty in OOD detection for text classification tasks. We propose an inexpensive framework that adopts both auxiliary outliers and pseudo off-manifold samples to train the model with prior knowledge of a certain class, which has high vacuity for OOD samples. Extensive empirical experiments demonstrate that our model based on evidential uncertainty outperforms other counterparts for detecting OOD examples. Our approach can be easily deployed to traditional recurrent neural networks and fine-tuned pre-trained transformers.
Approaches based on deep neural networks have achieved striking performance when testing data and training data share similar distribution, but can significantly fail otherwise. Therefore, eliminating the impact of distribution shifts between training and testing data is crucial for building performance-promising deep models. Conventional methods assume either the known heterogeneity of training data (e.g. domain labels) or the approximately equal capacities of different domains. In this paper, we consider a more challenging case where neither of the above assumptions holds. We propose to address this problem by removing the dependencies between features via learning weights for training samples, which helps deep models get rid of spurious correlations and, in turn, concentrate more on the true connection between discriminative features and labels. Extensive experiments clearly demonstrate the effectiveness of our method on multiple distribution generalization benchmarks compared with state-of-the-art counterparts. Through extensive experiments on distribution generalization benchmarks including PACS, VLCS, MNIST-M, and NICO, we show the effectiveness of our method compared with state-of-the-art counterparts.
Visual salient object detection (SOD) aims at finding the salient object(s) that attract human attention, while camouflaged object detection (COD) on the contrary intends to discover the camouflaged object(s) that hidden in the surrounding. In this paper, we propose a paradigm of leveraging the contradictory information to enhance the detection ability of both salient object detection and camouflaged object detection. We start by exploiting the easy positive samples in the COD dataset to serve as hard positive samples in the SOD task to improve the robustness of the SOD model. Then, we introduce a similarity measure module to explicitly model the contradicting attributes of these two tasks. Furthermore, considering the uncertainty of labeling in both tasks' datasets, we propose an adversarial learning network to achieve both higher order similarity measure and network confidence estimation. Experimental results on benchmark datasets demonstrate that our solution leads to state-of-the-art (SOTA) performance for both tasks.
Modern online advertising systems inevitably rely on personalization methods, such as click-through rate (CTR) prediction. Recent progress in CTR prediction enjoys the rich representation capabilities of deep learning and achieves great success in large-scale industrial applications. However, these methods can suffer from lack of exploration. Another line of prior work addresses the exploration-exploitation trade-off problem with contextual bandit methods, which are less studied in the industry recently due to the difficulty in extending their flexibility with deep models. In this paper, we propose a novel Deep Uncertainty-Aware Learning (DUAL) method to learn deep CTR models based on Gaussian processes, which can provide efficient uncertainty estimations along with the CTR predictions while maintaining the flexibility of deep neural networks. By linking the ability to estimate predictive uncertainties of DUAL to well-known bandit algorithms, we further present DUAL-based Ad-ranking strategies to boost up long-term utilities such as the social welfare in advertising systems. Experimental results on several public datasets demonstrate the effectiveness of our methods. Remarkably, an online A/B test deployed in the Alibaba display advertising platform shows an $8.2\%$ social welfare improvement and an $8.0\%$ revenue lift.
Data augmentation has been widely used for training deep learning systems for medical image segmentation and plays an important role in obtaining robust and transformation-invariant predictions. However, it has seldom been used at test time for segmentation and not been formulated in a consistent mathematical framework. In this paper, we first propose a theoretical formulation of test-time augmentation for deep learning in image recognition, where the prediction is obtained through estimating its expectation by Monte Carlo simulation with prior distributions of parameters in an image acquisition model that involves image transformations and noise. We then propose a novel uncertainty estimation method based on the formulated test-time augmentation. Experiments with segmentation of fetal brains and brain tumors from 2D and 3D Magnetic Resonance Images (MRI) showed that 1) our test-time augmentation outperforms a single-prediction baseline and dropout-based multiple predictions, and 2) it provides a better uncertainty estimation than calculating the model-based uncertainty alone and helps to reduce overconfident incorrect predictions.
We propose the Wasserstein Auto-Encoder (WAE)---a new algorithm for building a generative model of the data distribution. WAE minimizes a penalized form of the Wasserstein distance between the model distribution and the target distribution, which leads to a different regularizer than the one used by the Variational Auto-Encoder (VAE). This regularizer encourages the encoded training distribution to match the prior. We compare our algorithm with several other techniques and show that it is a generalization of adversarial auto-encoders (AAE). Our experiments show that WAE shares many of the properties of VAEs (stable training, encoder-decoder architecture, nice latent manifold structure) while generating samples of better quality, as measured by the FID score.
Methods that align distributions by minimizing an adversarial distance between them have recently achieved impressive results. However, these approaches are difficult to optimize with gradient descent and they often do not converge well without careful hyperparameter tuning and proper initialization. We investigate whether turning the adversarial min-max problem into an optimization problem by replacing the maximization part with its dual improves the quality of the resulting alignment and explore its connections to Maximum Mean Discrepancy. Our empirical results suggest that using the dual formulation for the restricted family of linear discriminators results in a more stable convergence to a desirable solution when compared with the performance of a primal min-max GAN-like objective and an MMD objective under the same restrictions. We test our hypothesis on the problem of aligning two synthetic point clouds on a plane and on a real-image domain adaptation problem on digits. In both cases, the dual formulation yields an iterative procedure that gives more stable and monotonic improvement over time.
In this paper, we study the optimal convergence rate for distributed convex optimization problems in networks. We model the communication restrictions imposed by the network as a set of affine constraints and provide optimal complexity bounds for four different setups, namely: the function $F(\xb) \triangleq \sum_{i=1}^{m}f_i(\xb)$ is strongly convex and smooth, either strongly convex or smooth or just convex. Our results show that Nesterov's accelerated gradient descent on the dual problem can be executed in a distributed manner and obtains the same optimal rates as in the centralized version of the problem (up to constant or logarithmic factors) with an additional cost related to the spectral gap of the interaction matrix. Finally, we discuss some extensions to the proposed setup such as proximal friendly functions, time-varying graphs, improvement of the condition numbers.