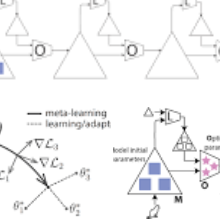
Physics-Informed Neural Network (PINN) has proven itself a powerful tool to obtain the numerical solutions of nonlinear partial differential equations (PDEs) leveraging the expressivity of deep neural networks and the computing power of modern heterogeneous hardware. However, its training is still time-consuming, especially in the multi-query and real-time simulation settings, and its parameterization often overly excessive. In this paper, we propose the Generative Pre-Trained PINN (GPT-PINN) to mitigate both challenges in the setting of parametric PDEs. GPT-PINN represents a brand-new meta-learning paradigm for parametric systems. As a network of networks, its outer-/meta-network is hyper-reduced with only one hidden layer having significantly reduced number of neurons. Moreover, its activation function at each hidden neuron is a (full) PINN pre-trained at a judiciously selected system configuration. The meta-network adaptively ``learns'' the parametric dependence of the system and ``grows'' this hidden layer one neuron at a time. In the end, by encompassing a very small number of networks trained at this set of adaptively-selected parameter values, the meta-network is capable of generating surrogate solutions for the parametric system across the entire parameter domain accurately and efficiently.
相關內容
High-energy collisions at the Large Hadron Collider (LHC) provide valuable insights into open questions in particle physics. However, detector effects must be corrected before measurements can be compared to certain theoretical predictions or measurements from other detectors. Methods to solve this \textit{inverse problem} of mapping detector observations to theoretical quantities of the underlying collision are essential parts of many physics analyses at the LHC. We investigate and compare various generative deep learning methods to approximate this inverse mapping. We introduce a novel unified architecture, termed latent variation diffusion models, which combines the latent learning of cutting-edge generative art approaches with an end-to-end variational framework. We demonstrate the effectiveness of this approach for reconstructing global distributions of theoretical kinematic quantities, as well as for ensuring the adherence of the learned posterior distributions to known physics constraints. Our unified approach achieves a distribution-free distance to the truth of over 20 times less than non-latent state-of-the-art baseline and 3 times less than traditional latent diffusion models.
Automated program repair is a crucial task for improving the efficiency of software developers. Recently, neural-based techniques have demonstrated significant promise in generating correct patches for buggy code snippets. However, most existing approaches arbitrarily treat the buggy context without any analysis to capture the semantic relationship between the buggy statement and its context. Additionally, we observe that existing neural models may output an unaltered patch consistent with the input buggy code snippet, which fails to be the correct human-written one for fixing the given bug. To address the aforementioned limitations, we present in this paper a novel neural program repair framework called \approach, which adapts the general pre-trained language model for fixing single-line Java bugs. We make the first attempt to use program slicing to extract contextual information directly related to the given buggy statement as repair ingredients from the corresponding program dependence graph and eliminate unaltered patches using an intuitive but effective filter mechanism. We demonstrate the effectiveness of \approach on five benchmarks when compared with state-of-the-art baselines.
Given the facts of the extensiveness of multi-material diffusion problems and the inability of the standard PINN(Physics-Informed Neural Networks) method for such problems, in this paper we present a novel PINN method that can accurately solve the multi-material diffusion equation. The new method applies continuity conditions at the material interface derived from the property of the diffusion equation, and combines the distinctive spatial separation strategy and the loss term normalization strategy to solve the problem that the residual points cannot be arranged at the material interface, the problem that it is difficult to express non-smooth functions with a single neural network, and the problem that the neural network is difficult to optimize the loss function with different magnitudes of loss terms, which finally provides the available prediction function for a class of multi-material diffusion problems. Numerical experiments verify the robustness and effectiveness of the new method.
In numerous robotics and mechanical engineering applications, among others, data is often constrained on smooth manifolds due to the presence of rotational degrees of freedom. Common datadriven and learning-based methods such as neural ordinary differential equations (ODEs), however, typically fail to satisfy these manifold constraints and perform poorly for these applications. To address this shortcoming, in this paper we study a class of neural ordinary differential equations that, by design, leave a given manifold invariant, and characterize their properties by leveraging the controllability properties of control affine systems. In particular, using a result due to Agrachev and Caponigro on approximating diffeomorphisms with flows of feedback control systems, we show that any map that can be represented as the flow of a manifold-constrained dynamical system can also be approximated using the flow of manifold-constrained neural ODE, whenever a certain controllability condition is satisfied. Additionally, we show that this universal approximation property holds when the neural ODE has limited width in each layer, thus leveraging the depth of network instead for approximation. We verify our theoretical findings using numerical experiments on PyTorch for the manifolds S2 and the 3-dimensional orthogonal group SO(3), which are model manifolds for mechanical systems such as spacecrafts and satellites. We also compare the performance of the manifold invariant neural ODE with classical neural ODEs that ignore the manifold invariant properties and show the superiority of our approach in terms of accuracy and sample complexity.
Solving Partial Differential Equations (PDEs) is the core of many fields of science and engineering. While classical approaches are often prohibitively slow, machine learning models often fail to incorporate complete system information. Over the past few years, transformers have had a significant impact on the field of Artificial Intelligence and have seen increased usage in PDE applications. However, despite their success, transformers currently lack integration with physics and reasoning. This study aims to address this issue by introducing PITT: Physics Informed Token Transformer. The purpose of PITT is to incorporate the knowledge of physics by embedding partial differential equations (PDEs) into the learning process. PITT uses an equation tokenization method to learn an analytically-driven numerical update operator. By tokenizing PDEs and embedding partial derivatives, the transformer models become aware of the underlying knowledge behind physical processes. To demonstrate this, PITT is tested on challenging PDE neural operators in both 1D and 2D prediction tasks. The results show that PITT outperforms the popular Fourier Neural Operator and has the ability to extract physically relevant information from governing equations.
We propose gradient-enhanced PINNs based on transfer learning (TL-gPINNs) for inverse problems of the function coefficient discovery in order to overcome deficiency of the discrete characterization of the PDE loss in neural networks and improve accuracy of function feature description, which offers a new angle of view for gPINNs. The TL-gPINN algorithm is applied to infer the unknown variable coefficients of various forms (the polynomial, trigonometric function, hyperbolic function and fractional polynomial) and multiple variable coefficients simultaneously with abundant soliton solutions for the well-known variable coefficient nonlinear Schr\"{o}odinger equation. Compared with the PINN and gPINN, TL-gPINN yields considerable improvement in accuracy. Moreover, our method leverages the advantage of the transfer learning technique, which can help to mitigate the problem of inefficiency caused by extra loss terms of the gradient. Numerical results fully demonstrate the effectiveness of the TL-gPINN method in significant accuracy enhancement, and it also outperforms gPINN in efficiency even when the training data was corrupted with different levels of noise or hyper-parameters of neural networks are arbitrarily changed.
Emerging technologies like hypersonic aircraft, space exploration vehicles, and batteries avail fluid circulation in embedded microvasculatures for efficient thermal regulation. Modeling is vital during these engineered systems' design and operational phases. However, many challenges exist in developing a modeling framework. What is lacking is an accurate framework that (i) captures sharp jumps in the thermal flux across complex vasculature layouts, (ii) deals with oblique derivatives (involving tangential and normal components), (iii) handles nonlinearity because of radiative heat transfer, (iv) provides a high-speed forecast for real-time monitoring, and (v) facilitates robust inverse modeling. This paper addresses these challenges by availing the power of physics-informed neural networks (PINNs). We develop a fast, reliable, and accurate Scientific Machine Learning (SciML) framework for vascular-based thermal regulation -- called CoolPINNs: a PINNs-based modeling framework for active cooling. The proposed mesh-less framework elegantly overcomes all the mentioned challenges. The significance of the reported research is multi-fold. First, the framework is valuable for real-time monitoring of thermal regulatory systems because of rapid forecasting. Second, researchers can address complex thermoregulation designs inasmuch as the approach is mesh-less. Finally, the framework facilitates systematic parameter identification and inverse modeling studies, perhaps the current framework's most significant utility.
Graphs are important data representations for describing objects and their relationships, which appear in a wide diversity of real-world scenarios. As one of a critical problem in this area, graph generation considers learning the distributions of given graphs and generating more novel graphs. Owing to their wide range of applications, generative models for graphs, which have a rich history, however, are traditionally hand-crafted and only capable of modeling a few statistical properties of graphs. Recent advances in deep generative models for graph generation is an important step towards improving the fidelity of generated graphs and paves the way for new kinds of applications. This article provides an extensive overview of the literature in the field of deep generative models for graph generation. Firstly, the formal definition of deep generative models for the graph generation and the preliminary knowledge are provided. Secondly, taxonomies of deep generative models for both unconditional and conditional graph generation are proposed respectively; the existing works of each are compared and analyzed. After that, an overview of the evaluation metrics in this specific domain is provided. Finally, the applications that deep graph generation enables are summarized and five promising future research directions are highlighted.
Designing and generating new data under targeted properties has been attracting various critical applications such as molecule design, image editing and speech synthesis. Traditional hand-crafted approaches heavily rely on expertise experience and intensive human efforts, yet still suffer from the insufficiency of scientific knowledge and low throughput to support effective and efficient data generation. Recently, the advancement of deep learning induces expressive methods that can learn the underlying representation and properties of data. Such capability provides new opportunities in figuring out the mutual relationship between the structural patterns and functional properties of the data and leveraging such relationship to generate structural data given the desired properties. This article provides a systematic review of this promising research area, commonly known as controllable deep data generation. Firstly, the potential challenges are raised and preliminaries are provided. Then the controllable deep data generation is formally defined, a taxonomy on various techniques is proposed and the evaluation metrics in this specific domain are summarized. After that, exciting applications of controllable deep data generation are introduced and existing works are experimentally analyzed and compared. Finally, the promising future directions of controllable deep data generation are highlighted and five potential challenges are identified.
Unsupervised domain adaptation has recently emerged as an effective paradigm for generalizing deep neural networks to new target domains. However, there is still enormous potential to be tapped to reach the fully supervised performance. In this paper, we present a novel active learning strategy to assist knowledge transfer in the target domain, dubbed active domain adaptation. We start from an observation that energy-based models exhibit free energy biases when training (source) and test (target) data come from different distributions. Inspired by this inherent mechanism, we empirically reveal that a simple yet efficient energy-based sampling strategy sheds light on selecting the most valuable target samples than existing approaches requiring particular architectures or computation of the distances. Our algorithm, Energy-based Active Domain Adaptation (EADA), queries groups of targe data that incorporate both domain characteristic and instance uncertainty into every selection round. Meanwhile, by aligning the free energy of target data compact around the source domain via a regularization term, domain gap can be implicitly diminished. Through extensive experiments, we show that EADA surpasses state-of-the-art methods on well-known challenging benchmarks with substantial improvements, making it a useful option in the open world. Code is available at //github.com/BIT-DA/EADA.