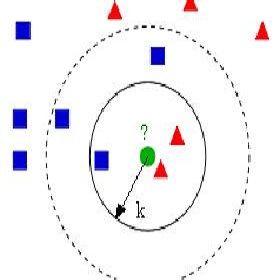
A Shared Nearest Neighbor (SNN) graph is a type of graph construction using shared nearest neighbor information, which is a secondary similarity measure based on the rankings induced by a primary $k$-nearest neighbor ($k$-NN) measure. SNN measures have been touted as being less prone to the curse of dimensionality than conventional distance measures, and thus methods using SNN graphs have been widely used in applications, particularly in clustering high-dimensional data sets and in finding outliers in subspaces of high dimensional data. Despite this, the theoretical study of SNN graphs and graph Laplacians remains unexplored. In this pioneering work, we make the first contribution in this direction. We show that large scale asymptotics of an SNN graph Laplacian reach a consistent continuum limit; this limit is the same as that of a $k$-NN graph Laplacian. Moreover, we show that the pointwise convergence rate of the graph Laplacian is linear with respect to $(k/n)^{1/m}$ with high probability.
相關內容
We are interested in the nonparametric estimation of the probability density of price returns, using the kernel approach. The output of the method heavily relies on the selection of a bandwidth parameter. Many selection methods have been proposed in the statistical literature. We put forward an alternative selection method based on a criterion coming from information theory and from the physics of complex systems: the bandwidth to be selected maximizes a new measure of complexity, with the aim of avoiding both overfitting and underfitting. We review existing methods of bandwidth selection and show that they lead to contradictory conclusions regarding the complexity of the probability distribution of price returns. This has also some striking consequences in the evaluation of the relevance of the efficient market hypothesis. We apply these methods to real financial data, focusing on the Bitcoin.
Empirical best prediction (EBP) is a well-known method for producing reliable proportion estimates when the primary data source provides only small or no sample from finite populations. There are at least two potential challenges encountered in implementing the existing EBP methodology. First, one must accurately link the sample to the finite population frame. This may be a difficult or even impossible task because of absence of identifiers that can be used to link sample and the frame. Secondly, the finite population frame typically contains limited auxiliary variables, which may not be adequate for building a reasonable working predictive model. We propose a data linkage approach in which we replace the finite population frame by a big sample that does not have the outcome binary variable of interest, but has a large set of auxiliary variables. Our proposed method calls for fitting the assumed model using data from the smaller sample, imputing the outcome variable for all the units of the big sample, and then finally using these imputed values to obtain standard weighted proportion using the big sample. We develop a new adjusted maximum likelihood method to avoid estimates of model variance on the boundary encountered in the commonly used in maximum likelihood estimation method. We propose an estimator of mean squared prediction error (MSPE) using a parametric bootstrap method and address computational issues by developing efficient EM algorithm. We illustrate the proposed methodology in the context of election projection for small areas.
The graph traversal edit distance (GTED) is an elegant distance measure defined as the minimum edit distance between strings reconstructed from Eulerian trails in two edge-labeled graphs. GTED can be used to infer evolutionary relationships between species by comparing de Bruijn graphs directly without the computationally costly and error-prone process of genome assembly. Ebrahimpour Boroojeny et al.~(2018) suggest two ILP formulations for GTED and claim that GTED is polynomially solvable because the linear programming relaxation of one of the ILP always yields optimal integer solutions. The result that GTED is polynomially solvable is contradictory to the complexity results of existing string-to-graph matching problems. We resolve this conflict in complexity results by proving that GTED is NP-complete and showing that the ILPs proposed by Ebrahimpour Boroojeny et al. do not solve GTED but instead solve for a lower bound of GTED and are not solvable in polynomial time. In addition, we provide the first two, correct ILP formulations of GTED and evaluate their empirical efficiency. These results provide solid algorithmic foundations for comparing genome graphs and point to the direction of approximation heuristics. The source code to reproduce experimental results is available at //github.com/Kingsford-Group/gtednewilp/.
Knowledge graphs represent factual knowledge about the world as relationships between concepts and are critical for intelligent decision making in enterprise applications. New knowledge is inferred from the existing facts in the knowledge graphs by encoding the concepts and relations into low-dimensional feature vector representations. The most effective representations for this task, called Knowledge Graph Embeddings (KGE), are learned through neural network architectures. Due to their impressive predictive performance, they are increasingly used in high-impact domains like healthcare, finance and education. However, are the black-box KGE models adversarially robust for use in domains with high stakes? This thesis argues that state-of-the-art KGE models are vulnerable to data poisoning attacks, that is, their predictive performance can be degraded by systematically crafted perturbations to the training knowledge graph. To support this argument, two novel data poisoning attacks are proposed that craft input deletions or additions at training time to subvert the learned model's performance at inference time. These adversarial attacks target the task of predicting the missing facts in knowledge graphs using KGE models, and the evaluation shows that the simpler attacks are competitive with or outperform the computationally expensive ones. The thesis contributions not only highlight and provide an opportunity to fix the security vulnerabilities of KGE models, but also help to understand the black-box predictive behaviour of KGE models.
Recently many efforts have been devoted to applying graph neural networks (GNNs) to molecular property prediction which is a fundamental task for computational drug and material discovery. One of major obstacles to hinder the successful prediction of molecule property by GNNs is the scarcity of labeled data. Though graph contrastive learning (GCL) methods have achieved extraordinary performance with insufficient labeled data, most focused on designing data augmentation schemes for general graphs. However, the fundamental property of a molecule could be altered with the augmentation method (like random perturbation) on molecular graphs. Whereas, the critical geometric information of molecules remains rarely explored under the current GNN and GCL architectures. To this end, we propose a novel graph contrastive learning method utilizing the geometry of the molecule across 2D and 3D views, which is named GeomGCL. Specifically, we first devise a dual-view geometric message passing network (GeomMPNN) to adaptively leverage the rich information of both 2D and 3D graphs of a molecule. The incorporation of geometric properties at different levels can greatly facilitate the molecular representation learning. Then a novel geometric graph contrastive scheme is designed to make both geometric views collaboratively supervise each other to improve the generalization ability of GeomMPNN. We evaluate GeomGCL on various downstream property prediction tasks via a finetune process. Experimental results on seven real-life molecular datasets demonstrate the effectiveness of our proposed GeomGCL against state-of-the-art baselines.
Graph Neural Networks (GNNs) have been studied from the lens of expressive power and generalization. However, their optimization properties are less well understood. We take the first step towards analyzing GNN training by studying the gradient dynamics of GNNs. First, we analyze linearized GNNs and prove that despite the non-convexity of training, convergence to a global minimum at a linear rate is guaranteed under mild assumptions that we validate on real-world graphs. Second, we study what may affect the GNNs' training speed. Our results show that the training of GNNs is implicitly accelerated by skip connections, more depth, and/or a good label distribution. Empirical results confirm that our theoretical results for linearized GNNs align with the training behavior of nonlinear GNNs. Our results provide the first theoretical support for the success of GNNs with skip connections in terms of optimization, and suggest that deep GNNs with skip connections would be promising in practice.
Sequential recommendation (SR) is to accurately recommend a list of items for a user based on her current accessed ones. While new-coming users continuously arrive in the real world, one crucial task is to have inductive SR that can produce embeddings of users and items without re-training. Given user-item interactions can be extremely sparse, another critical task is to have transferable SR that can transfer the knowledge derived from one domain with rich data to another domain. In this work, we aim to present the holistic SR that simultaneously accommodates conventional, inductive, and transferable settings. We propose a novel deep learning-based model, Relational Temporal Attentive Graph Neural Networks (RetaGNN), for holistic SR. The main idea of RetaGNN is three-fold. First, to have inductive and transferable capabilities, we train a relational attentive GNN on the local subgraph extracted from a user-item pair, in which the learnable weight matrices are on various relations among users, items, and attributes, rather than nodes or edges. Second, long-term and short-term temporal patterns of user preferences are encoded by a proposed sequential self-attention mechanism. Third, a relation-aware regularization term is devised for better training of RetaGNN. Experiments conducted on MovieLens, Instagram, and Book-Crossing datasets exhibit that RetaGNN can outperform state-of-the-art methods under conventional, inductive, and transferable settings. The derived attention weights also bring model explainability.
Many real-world applications require the prediction of long sequence time-series, such as electricity consumption planning. Long sequence time-series forecasting (LSTF) demands a high prediction capacity of the model, which is the ability to capture precise long-range dependency coupling between output and input efficiently. Recent studies have shown the potential of Transformer to increase the prediction capacity. However, there are several severe issues with Transformer that prevent it from being directly applicable to LSTF, such as quadratic time complexity, high memory usage, and inherent limitation of the encoder-decoder architecture. To address these issues, we design an efficient transformer-based model for LSTF, named Informer, with three distinctive characteristics: (i) a $ProbSparse$ Self-attention mechanism, which achieves $O(L \log L)$ in time complexity and memory usage, and has comparable performance on sequences' dependency alignment. (ii) the self-attention distilling highlights dominating attention by halving cascading layer input, and efficiently handles extreme long input sequences. (iii) the generative style decoder, while conceptually simple, predicts the long time-series sequences at one forward operation rather than a step-by-step way, which drastically improves the inference speed of long-sequence predictions. Extensive experiments on four large-scale datasets demonstrate that Informer significantly outperforms existing methods and provides a new solution to the LSTF problem.
Graph convolutional network (GCN) has been successfully applied to many graph-based applications; however, training a large-scale GCN remains challenging. Current SGD-based algorithms suffer from either a high computational cost that exponentially grows with number of GCN layers, or a large space requirement for keeping the entire graph and the embedding of each node in memory. In this paper, we propose Cluster-GCN, a novel GCN algorithm that is suitable for SGD-based training by exploiting the graph clustering structure. Cluster-GCN works as the following: at each step, it samples a block of nodes that associate with a dense subgraph identified by a graph clustering algorithm, and restricts the neighborhood search within this subgraph. This simple but effective strategy leads to significantly improved memory and computational efficiency while being able to achieve comparable test accuracy with previous algorithms. To test the scalability of our algorithm, we create a new Amazon2M data with 2 million nodes and 61 million edges which is more than 5 times larger than the previous largest publicly available dataset (Reddit). For training a 3-layer GCN on this data, Cluster-GCN is faster than the previous state-of-the-art VR-GCN (1523 seconds vs 1961 seconds) and using much less memory (2.2GB vs 11.2GB). Furthermore, for training 4 layer GCN on this data, our algorithm can finish in around 36 minutes while all the existing GCN training algorithms fail to train due to the out-of-memory issue. Furthermore, Cluster-GCN allows us to train much deeper GCN without much time and memory overhead, which leads to improved prediction accuracy---using a 5-layer Cluster-GCN, we achieve state-of-the-art test F1 score 99.36 on the PPI dataset, while the previous best result was 98.71 by [16]. Our codes are publicly available at //github.com/google-research/google-research/tree/master/cluster_gcn.
In many real-world network datasets such as co-authorship, co-citation, email communication, etc., relationships are complex and go beyond pairwise. Hypergraphs provide a flexible and natural modeling tool to model such complex relationships. The obvious existence of such complex relationships in many real-world networks naturaly motivates the problem of learning with hypergraphs. A popular learning paradigm is hypergraph-based semi-supervised learning (SSL) where the goal is to assign labels to initially unlabeled vertices in a hypergraph. Motivated by the fact that a graph convolutional network (GCN) has been effective for graph-based SSL, we propose HyperGCN, a novel GCN for SSL on attributed hypergraphs. Additionally, we show how HyperGCN can be used as a learning-based approach for combinatorial optimisation on NP-hard hypergraph problems. We demonstrate HyperGCN's effectiveness through detailed experimentation on real-world hypergraphs.