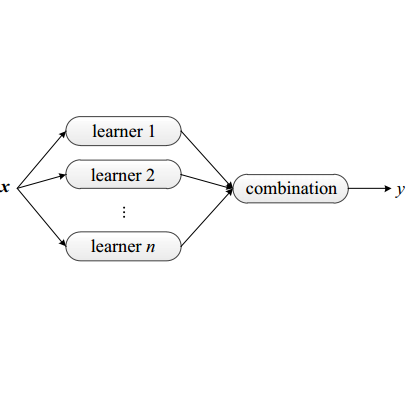
Regression algorithms are regularly used for improving the accuracy of satellite precipitation products. In this context, satellite precipitation and topography data are the predictor variables, and gauged-measured precipitation data are the dependent variables. Alongside this, it is increasingly recognised in many fields that combinations of algorithms through ensemble learning can lead to substantial predictive performance improvements. Still, a sufficient number of ensemble learners for improving the accuracy of satellite precipitation products and their large-scale comparison are currently missing from the literature. In this study, we work towards filling in this specific gap by proposing 11 new ensemble learners in the field and by extensively comparing them. We apply the ensemble learners to monthly data from the PERSIANN (Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks) and IMERG (Integrated Multi-satellitE Retrievals for GPM) gridded datasets that span over a 15-year period and over the entire the contiguous United States (CONUS). We also use gauge-measured precipitation data from the Global Historical Climatology Network monthly database, version 2 (GHCNm). The ensemble learners combine the predictions of six machine learning regression algorithms (base learners), namely the multivariate adaptive regression splines (MARS), multivariate adaptive polynomial splines (poly-MARS), random forests (RF), gradient boosting machines (GBM), extreme gradient boosting (XGBoost) and Bayesian regularized neural networks (BRNN), and each of them is based on a different combiner. The combiners include the equal-weight combiner, the median combiner, two best learners and seven variants of a sophisticated stacking method. The latter stacks a regression algorithm on top of the base learners to combine their independent predictions...
相關內容
The trace plot is seldom used in meta-analysis, yet it is a very informative plot. In this article we define and illustrate what the trace plot is, and discuss why it is important. The Bayesian version of the plot combines the posterior density of tau, the between-study standard deviation, and the shrunken estimates of the study effects as a function of tau. With a small or moderate number of studies, tau is not estimated with much precision, and parameter estimates and shrunken study effect estimates can vary widely depending on the correct value of tau. The trace plot allows visualization of the sensitivity to tau along with a plot that shows which values of tau are plausible and which are implausible. A comparable frequentist or empirical Bayes version provides similar results. The concepts are illustrated using examples in meta-analysis and meta-regression; implementaton in R is facilitated in a Bayesian or frequentist framework using the bayesmeta and metafor packages, respectively.
Many approaches have been proposed to use diffusion models to augment training datasets for downstream tasks, such as classification. However, diffusion models are themselves trained on large datasets, often with noisy annotations, and it remains an open question to which extent these models contribute to downstream classification performance. In particular, it remains unclear if they generalize enough to improve over directly using the additional data of their pre-training process for augmentation. We systematically evaluate a range of existing methods to generate images from diffusion models and study new extensions to assess their benefit for data augmentation. Personalizing diffusion models towards the target data outperforms simpler prompting strategies. However, using the pre-training data of the diffusion model alone, via a simple nearest-neighbor retrieval procedure, leads to even stronger downstream performance. Our study explores the potential of diffusion models in generating new training data, and surprisingly finds that these sophisticated models are not yet able to beat a simple and strong image retrieval baseline on simple downstream vision tasks.
We consider M-estimators and derive supremal-inequalities of exponential-or polynomial type according as a boundedness- or a moment-condition is fulfilled. This enables us to derive rates of r-complete convergence and also to show r-qick convergence in the sense of Strasser.
Regression with random data objects is becoming increasingly common in modern data analysis. Unfortunately, like the traditional regression setting with Euclidean data, random response regression is not immune to the trouble caused by unusual observations. A metric Cook's distance extending the classical Cook's distances of Cook (1977) to general metric-valued response objects is proposed. The performance of the metric Cook's distance in both Euclidean and non-Euclidean response regression with Euclidean predictors is demonstrated in an extensive experimental study. A real data analysis of county-level COVID-19 transmission in the United States also illustrates the usefulness of this method in practice.
Threshold selection is a fundamental problem in any threshold-based extreme value analysis. While models are asymptotically motivated, selecting an appropriate threshold for finite samples can be difficult through standard methods. Inference can also be highly sensitive to the choice of threshold. Too low a threshold choice leads to bias in the fit of the extreme value model, while too high a choice leads to unnecessary additional uncertainty in the estimation of model parameters. In this paper, we develop a novel methodology for automated threshold selection that directly tackles this bias-variance trade-off. We also develop a method to account for the uncertainty in this threshold choice and propagate this uncertainty through to high quantile inference. Through a simulation study, we demonstrate the effectiveness of our method for threshold selection and subsequent extreme quantile estimation. We apply our method to the well-known, troublesome example of the River Nidd dataset.
We consider the problem of using SciML to predict solutions of high Mach fluid flows over irregular geometries. In this setting, data is limited, and so it is desirable for models to perform well in the low-data setting. We show that Neural Basis Functions (NBF), which learns a basis of behavior modes from the data and then uses this basis to make predictions, is more effective than a basis-unaware baseline model. In addition, we identify continuing challenges in the space of predicting solutions for this type of problem.
We analyse the geometric instability of embeddings produced by graph neural networks (GNNs). Existing methods are only applicable for small graphs and lack context in the graph domain. We propose a simple, efficient and graph-native Graph Gram Index (GGI) to measure such instability which is invariant to permutation, orthogonal transformation, translation and order of evaluation. This allows us to study the varying instability behaviour of GNN embeddings on large graphs for both node classification and link prediction.
Linear regression and classification methods with repeated functional data are considered. For each statistical unit in the sample, a real-valued parameter is observed over time under different conditions. Two regression methods based on fusion penalties are presented. The first one is a generalization of the variable fusion methodology based on the 1-nearest neighbor. The second one, called group fusion lasso, assumes some grouping structure of conditions and allows for homogeneity among the regression coefficient functions within groups. A finite sample numerical simulation and an application on EEG data are presented.
A novel method for detecting faults in power grids using a graph neural network (GNN) has been developed, aimed at enhancing intelligent fault diagnosis in network operation and maintenance. This GNN-based approach identifies faulty nodes within the power grid through a specialized electrical feature extraction model coupled with a knowledge graph. Incorporating temporal data, the method leverages the status of nodes from preceding and subsequent time periods to aid in current fault detection. To validate the effectiveness of this GNN in extracting node features, a correlation analysis of the output features from each node within the neural network layer was conducted. The results from experiments show that this method can accurately locate fault nodes in simulated scenarios with a remarkable 99.53% accuracy. Additionally, the graph neural network's feature modeling allows for a qualitative examination of how faults spread across nodes, providing valuable insights for analyzing fault nodes.
The remarkable practical success of deep learning has revealed some major surprises from a theoretical perspective. In particular, simple gradient methods easily find near-optimal solutions to non-convex optimization problems, and despite giving a near-perfect fit to training data without any explicit effort to control model complexity, these methods exhibit excellent predictive accuracy. We conjecture that specific principles underlie these phenomena: that overparametrization allows gradient methods to find interpolating solutions, that these methods implicitly impose regularization, and that overparametrization leads to benign overfitting. We survey recent theoretical progress that provides examples illustrating these principles in simpler settings. We first review classical uniform convergence results and why they fall short of explaining aspects of the behavior of deep learning methods. We give examples of implicit regularization in simple settings, where gradient methods lead to minimal norm functions that perfectly fit the training data. Then we review prediction methods that exhibit benign overfitting, focusing on regression problems with quadratic loss. For these methods, we can decompose the prediction rule into a simple component that is useful for prediction and a spiky component that is useful for overfitting but, in a favorable setting, does not harm prediction accuracy. We focus specifically on the linear regime for neural networks, where the network can be approximated by a linear model. In this regime, we demonstrate the success of gradient flow, and we consider benign overfitting with two-layer networks, giving an exact asymptotic analysis that precisely demonstrates the impact of overparametrization. We conclude by highlighting the key challenges that arise in extending these insights to realistic deep learning settings.