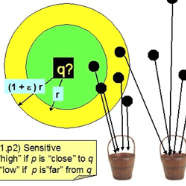
Extended differential privacy, a generalization of standard differential privacy (DP) using a general metric, has been widely studied to provide rigorous privacy guarantees while keeping high utility. However, existing works on extended DP are limited to few metrics, such as the Euclidean metric. Consequently, they have only a small number of applications, such as location-based services and document processing. In this paper, we propose a couple of mechanisms providing extended DP with a different metric: angular distance (or cosine distance). Our mechanisms are based on locality sensitive hashing (LSH), which can be applied to the angular distance and work well for personal data in a high-dimensional space. We theoretically analyze the privacy properties of our mechanisms, and prove extended DP for input data by taking into account that LSH preserves the original metric only approximately. We apply our mechanisms to friend matching based on high-dimensional personal data with angular distance in the local model, and evaluate our mechanisms using two real datasets. We show that LDP requires a very large privacy budget and that RAPPOR does not work in this application. Then we show that our mechanisms enable friend matching with high utility and rigorous privacy guarantees based on extended DP.
相關內容
In this paper, we focus on preserving differential privacy (DP) in continual learning (CL), in which we train ML models to learn a sequence of new tasks while memorizing previous tasks. We first introduce a notion of continual adjacent databases to bound the sensitivity of any data record participating in the training process of CL. Based upon that, we develop a new DP-preserving algorithm for CL with a data sampling strategy to quantify the privacy risk of training data in the well-known Averaged Gradient Episodic Memory (A-GEM) approach by applying a moments accountant. Our algorithm provides formal guarantees of privacy for data records across tasks in CL. Preliminary theoretical analysis and evaluations show that our mechanism tightens the privacy loss while maintaining a promising model utility.
Matrix completion is a prevailing collaborative filtering method for recommendation systems that requires the data offered by users to provide personalized service. However, due to insidious attacks and unexpected inference, the release of user data often raises serious privacy concerns. Most of the existing solutions focus on improving the privacy guarantee for general matrix completion. As a special case, in recommendation systems where the observations are binary, one-bit matrix completion covers a broad range of real-life situations. In this paper, we propose a novel framework for one-bit matrix completion under the differential privacy constraint. In this framework, we develop several perturbation mechanisms and analyze the privacy-accuracy trade-off offered by each mechanism. The experiments conducted on both synthetic and real-world datasets demonstrate that our proposed approaches can maintain high-level privacy with little loss of completion accuracy.
We introduce the multi-dimensional Skellam mechanism, a discrete differential privacy mechanism based on the difference of two independent Poisson random variables. To quantify its privacy guarantees, we analyze the privacy loss distribution via a numerical evaluation and provide a sharp bound on the R\'enyi divergence between two shifted Skellam distributions. While useful in both centralized and distributed privacy applications, we investigate how it can be applied in the context of federated learning with secure aggregation under communication constraints. Our theoretical findings and extensive experimental evaluations demonstrate that the Skellam mechanism provides the same privacy-accuracy trade-offs as the continuous Gaussian mechanism, even when the precision is low. More importantly, Skellam is closed under summation and sampling from it only requires sampling from a Poisson distribution -- an efficient routine that ships with all machine learning and data analysis software packages. These features, along with its discrete nature and competitive privacy-accuracy trade-offs, make it an attractive alternative to the newly introduced discrete Gaussian mechanism.
A maximum distance separable (MDS) array code is composed of $m\times (k+r)$ arrays such that any $k$ out of $k+r$ columns suffice to retrieve all the information symbols. Expanded-Blaum-Roth (EBR) codes and Expanded-Independent-Parity (EIP) codes are two classes of MDS array codes that can repair any one symbol in a column by locally accessing some other symbols within the column, where the number of symbols $m$ in a column is a prime number. By generalizing the constructions of EBR and EIP codes, we propose new MDS array codes, such that any one symbol can be locally recovered and the number of symbols in a column can be not only a prime number but also a power of an odd prime number. Also, we present an efficient encoding/decoding method for the proposed generalized EBR (GEBR) and generalized EIP (GEIP) codes based on the LU factorization of a Vandermonde matrix. We show that the proposed decoding method has less computational complexity than existing methods. Furthermore, we show that the proposed GEBR codes have both a larger minimum symbol distance and a larger recovery ability of erased lines for some parameters when compared to EBR codes. We show that EBR codes can recover any $r$ erased lines of a slope for any parameter $r$, which was an open problem in [2].
In deep learning with differential privacy (DP), the neural network achieves the privacy usually at the cost of slower convergence (and thus lower performance) than its non-private counterpart. This work gives the first convergence analysis of the DP deep learning, through the lens of training dynamics and the neural tangent kernel (NTK). Our convergence theory successfully characterizes the effects of two key components in the DP training: the per-sample clipping and the noise addition. Our analysis not only initiates a general principled framework to understand the DP deep learning with any network architecture and loss function, but also motivates a new clipping method -- the global clipping, that significantly improves the convergence, as well as preserves the same DP guarantee and computational efficiency as the existing method, which we term as local clipping. Theoretically speaking, we precisely characterize the effect of per-sample clipping on the NTK matrix and show that the noise level of DP optimizers does not affect the convergence in the gradient flow regime. In particular, the local clipping almost certainly breaks the positive semi-definiteness of NTK, which can be preserved by our global clipping. Consequently, DP gradient descent (GD) with global clipping converge monotonically to zero loss, which is often violated by the existing DP-GD. Notably, our analysis framework easily extends to other optimizers, e.g., DP-Adam. We demonstrate through numerous experiments that DP optimizers equipped with global clipping perform strongly on classification and regression tasks. In addition, our global clipping is surprisingly effective at learning calibrated classifiers, in contrast to the existing DP classifiers which are oftentimes over-confident and unreliable. Implementation-wise, the new clipping can be realized by inserting one line of code into the Pytorch Opacus library.
In recent years, the transformer has established itself as a workhorse in many applications ranging from natural language processing to reinforcement learning. Similarly, Bayesian deep learning has become the gold-standard for uncertainty estimation in safety-critical applications, where robustness and calibration are crucial. Surprisingly, no successful attempts to improve transformer models in terms of predictive uncertainty using Bayesian inference exist. In this work, we study this curiously underpopulated area of Bayesian transformers. We find that weight-space inference in transformers does not work well, regardless of the approximate posterior. We also find that the prior is at least partially at fault, but that it is very hard to find well-specified weight priors for these models. We hypothesize that these problems stem from the complexity of obtaining a meaningful mapping from weight-space to function-space distributions in the transformer. Therefore, moving closer to function-space, we propose a novel method based on the implicit reparameterization of the Dirichlet distribution to apply variational inference directly to the attention weights. We find that this proposed method performs competitively with our baselines.
Privacy and Byzantine resilience (BR) are two crucial requirements of modern-day distributed machine learning. The two concepts have been extensively studied individually but the question of how to combine them effectively remains unanswered. This paper contributes to addressing this question by studying the extent to which the distributed SGD algorithm, in the standard parameter-server architecture, can learn an accurate model despite (a) a fraction of the workers being malicious (Byzantine), and (b) the other fraction, whilst being honest, providing noisy information to the server to ensure differential privacy (DP). We first observe that the integration of standard practices in DP and BR is not straightforward. In fact, we show that many existing results on the convergence of distributed SGD under Byzantine faults, especially those relying on $(\alpha,f)$-Byzantine resilience, are rendered invalid when honest workers enforce DP. To circumvent this shortcoming, we revisit the theory of $(\alpha,f)$-BR to obtain an approximate convergence guarantee. Our analysis provides key insights on how to improve this guarantee through hyperparameter optimization. Essentially, our theoretical and empirical results show that (1) an imprudent combination of standard approaches to DP and BR might be fruitless, but (2) by carefully re-tuning the learning algorithm, we can obtain reasonable learning accuracy while simultaneously guaranteeing DP and BR.
We study query and computationally efficient planning algorithms with linear function approximation and a simulator. We assume that the agent only has local access to the simulator, meaning that the agent can only query the simulator at states that have been visited before. This setting is more practical than many prior works on reinforcement learning with a generative model. We propose an algorithm named confident Monte Carlo least square policy iteration (Confident MC-LSPI) for this setting. Under the assumption that the Q-functions of all deterministic policies are linear in known features of the state-action pairs, we show that our algorithm has polynomial query and computational complexities in the dimension of the features, the effective planning horizon and the targeted sub-optimality, while these complexities are independent of the size of the state space. One technical contribution of our work is the introduction of a novel proof technique that makes use of a virtual policy iteration algorithm. We use this method to leverage existing results on $\ell_\infty$-bounded approximate policy iteration to show that our algorithm can learn the optimal policy for the given initial state even only with local access to the simulator. We believe that this technique can be extended to broader settings beyond this work.
We present $\zeta$-DP, an extension of differential privacy (DP) to complex-valued functions. After introducing the complex Gaussian mechanism, whose properties we characterise in terms of $(\varepsilon, \delta)$-DP and R\'enyi-DP, we present $\zeta$-DP stochastic gradient descent ($\zeta$-DP-SGD), a variant of DP-SGD for training complex-valued neural networks. We experimentally evaluate $\zeta$-DP-SGD on three complex-valued tasks, i.e. electrocardiogram classification, speech classification and magnetic resonance imaging (MRI) reconstruction. Moreover, we provide $\zeta$-DP-SGD benchmarks for a large variety of complex-valued activation functions and on a complex-valued variant of the MNIST dataset. Our experiments demonstrate that DP training of complex-valued neural networks is possible with rigorous privacy guarantees and excellent utility.
Train machine learning models on sensitive user data has raised increasing privacy concerns in many areas. Federated learning is a popular approach for privacy protection that collects the local gradient information instead of real data. One way to achieve a strict privacy guarantee is to apply local differential privacy into federated learning. However, previous works do not give a practical solution due to three issues. First, the noisy data is close to its original value with high probability, increasing the risk of information exposure. Second, a large variance is introduced to the estimated average, causing poor accuracy. Last, the privacy budget explodes due to the high dimensionality of weights in deep learning models. In this paper, we proposed a novel design of local differential privacy mechanism for federated learning to address the abovementioned issues. It is capable of making the data more distinct from its original value and introducing lower variance. Moreover, the proposed mechanism bypasses the curse of dimensionality by splitting and shuffling model updates. A series of empirical evaluations on three commonly used datasets, MNIST, Fashion-MNIST and CIFAR-10, demonstrate that our solution can not only achieve superior deep learning performance but also provide a strong privacy guarantee at the same time.