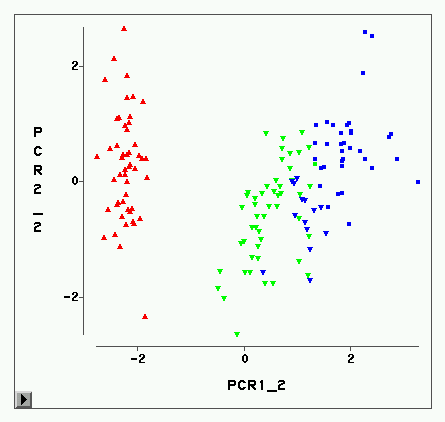
Compositional data are contemporarily defined as positive vectors, the ratios among whose elements are of interest to the researcher. Financial statement analysis by means of accounting ratios fulfils this definition to the letter. Compositional data analysis solves the major problems in statistical analysis of standard financial ratios at industry level, such as skewness, non-normality, non-linearity and dependence of the results on the choice of which accounting figure goes to the numerator and to the denominator of the ratio. In spite of this, compositional applications to financial statement analysis are still rare. In this article, we present some transformations within compositional data analysis that are particularly useful for financial statement analysis. We show how to compute industry or sub-industry means of standard financial ratios from a compositional perspective. We show how to visualise firms in an industry with a compositional biplot, to classify them with compositional cluster analysis and to relate financial and non-financial indicators with compositional regression models. We show an application to the accounting statements of Spanish wineries using DuPont analysis, and a step-by-step tutorial to the compositional freeware CoDaPack.
相關內容
The approach to analysing compositional data has been dominated by the use of logratio transformations, to ensure exact subcompositional coherence and, in some situations, exact isometry as well. A problem with this approach is that data zeros, found in most applications, have to be replaced to allow the logarithmic transformation. An alternative new approach, called the `chiPower' transformation, which allows data zeros, is to combine the standardization inherent in the chi-square distance in correspondence analysis, with the essential elements of the Box-Cox power transformation. The chiPower transformation is justified because it} defines between-sample distances that tend to logratio distances for strictly positive data as the power parameter tends to zero, and are then equivalent to transforming to logratios. For data with zeros, a value of the power can be identified that brings the chiPower transformation as close as possible to a logratio transformation, without having to substitute the zeros. Especially in the area of high-dimensional data, this alternative approach can present such a high level of coherence and isometry as to be a valid approach to the analysis of compositional data. Furthermore, in a supervised learning context, if the compositional variables serve as predictors of a response in a modelling framework, for example generalized linear models, then the power can be used as a tuning parameter in optimizing the accuracy of prediction through cross-validation. The chiPower-transformed variables have a straightforward interpretation, since they are each identified with single compositional parts, not ratios.
Bayesian linear mixed-effects models and Bayesian ANOVA are increasingly being used in the cognitive sciences to perform null hypothesis tests, where a null hypothesis that an effect is zero is compared with an alternative hypothesis that the effect exists and is different from zero. While software tools for Bayes factor null hypothesis tests are easily accessible, how to specify the data and the model correctly is often not clear. In Bayesian approaches, many authors use data aggregation at the by-subject level and estimate Bayes factors on aggregated data. Here, we use simulation-based calibration for model inference applied to several example experimental designs to demonstrate that, as with frequentist analysis, such null hypothesis tests on aggregated data can be problematic in Bayesian analysis. Specifically, when random slope variances differ (i.e., violated sphericity assumption), Bayes factors are too conservative for contrasts where the variance is small and they are too liberal for contrasts where the variance is large. Running Bayesian ANOVA on aggregated data can - if the sphericity assumption is violated - likewise lead to biased Bayes factor results. Moreover, Bayes factors for by-subject aggregated data are biased (too liberal) when random item slope variance is present but ignored in the analysis. These problems can be circumvented or reduced by running Bayesian linear mixed-effects models on non-aggregated data such as on individual trials, and by explicitly modeling the full random effects structure. Reproducible code is available from \url{//osf.io/mjf47/}.
The quantification of cognitive powers rests on identifying a behavioural task that depends on them. Such dependence cannot be assured, for the powers a task invokes cannot be experimentally controlled or constrained a priori, resulting in unknown vulnerability to failure of specificity and generalisability. Evaluating a compact version of Raven's Advanced Progressive Matrices (RAPM), a widely used clinical test of fluid intelligence, we show that LaMa, a self-supervised artificial neural network trained solely on the completion of partially masked images of natural environmental scenes, achieves human-level test scores a prima vista, without any task-specific inductive bias or training. Compared with cohorts of healthy and focally lesioned participants, LaMa exhibits human-like variation with item difficulty, and produces errors characteristic of right frontal lobe damage under degradation of its ability to integrate global spatial patterns. LaMa's narrow training and limited capacity -- comparable to the nervous system of the fruit fly -- suggest RAPM may be open to computationally simple solutions that need not necessarily invoke abstract reasoning.
The work of Kalman and Bucy has established a duality between filtering and optimal estimation in the context of time-continuous linear systems. This duality has recently been extended to time-continuous nonlinear systems in terms of an optimization problem constrained by a backward stochastic partial differential equation. Here we revisit this problem from the perspective of appropriate forward-backward stochastic differential equations. This approach sheds new light on the estimation problem and provides a unifying perspective. It is also demonstrated that certain formulations of the estimation problem lead to deterministic formulations similar to the linear Gaussian case as originally investigated by Kalman and Bucy. Finally, optimal control of partially observed diffusion processes is discussed as an application of the proposed estimators.
A Hadamard-Hitchcock decomposition of a multidimensional array is a decomposition that expresses the latter as a Hadamard product of several tensor rank decompositions. Such decompositions can encode probability distributions that arise from statistical graphical models associated to complete bipartite graphs with one layer of observed random variables and one layer of hidden ones, usually called restricted Boltzmann machines. We establish generic identifiability of Hadamard-Hitchcock decompositions by exploiting the reshaped Kruskal criterion for tensor rank decompositions. A flexible algorithm leveraging existing decomposition algorithms for tensor rank decomposition is introduced for computing a Hadamard-Hitchcock decomposition. Numerical experiments illustrate its computational performance and numerical accuracy.
The purpose of the paper is to provide a characterization of the error of the best polynomial approximation of composite functions in weighted spaces. Such a characterization is essential for the convergence analysis of numerical methods applied to non-linear problems or for numerical approaches that make use of regularization techniques to cure low smoothness of the solution. This result is obtained through an estimate of the derivatives of composite functions in weighted uniform norm.
Temporal irreversibility, often referred to as the arrow of time, is a fundamental concept in statistical mechanics. Markers of irreversibility also provide a powerful characterisation of information processing in biological systems. However, current approaches tend to describe temporal irreversibility in terms of a single scalar quantity, without disentangling the underlying dynamics that contribute to irreversibility. Here we propose a broadly applicable information-theoretic framework to characterise the arrow of time in multivariate time series, which yields qualitatively different types of irreversible information dynamics. This multidimensional characterisation reveals previously unreported high-order modes of irreversibility, and establishes a formal connection between recent heuristic markers of temporal irreversibility and metrics of information processing. We demonstrate the prevalence of high-order irreversibility in the hyperactive regime of a biophysical model of brain dynamics, showing that our framework is both theoretically principled and empirically useful. This work challenges the view of the arrow of time as a monolithic entity, enhancing both our theoretical understanding of irreversibility and our ability to detect it in practical applications.
It is desirable for statistical models to detect signals of interest independently of their position. If the data is generated by some smooth process, this additional structure should be taken into account. We introduce a new class of neural networks that are shift invariant and preserve smoothness of the data: functional neural networks (FNNs). For this, we use methods from functional data analysis (FDA) to extend multi-layer perceptrons and convolutional neural networks to functional data. We propose different model architectures, show that the models outperform a benchmark model from FDA in terms of accuracy and successfully use FNNs to classify electroencephalography (EEG) data.
Given $n$ independent and identically distributed observations and measuring the value of obtaining an additional observation in terms of Le Cam's notion of deficiency between experiments, we show for certain types of non-parametric experiments that the value of an additional observation decreases at a rate of $1/\sqrt{n}$. This is distinct from the known typical decrease at a rate of $1/n$ for parametric experiments and the non-decreasing value in the case of very large experiments. In particular, the rate of $1/\sqrt{n}$ holds for the experiment given by observing samples from a density about which we know only that it is bounded from below by some fixed constant. Thus there exists an experiment where the value of additional observations tends to zero but for which no estimator that is consistent (in total variation distance) exists.
Surgical instrument segmentation is recognised as a key enabler to provide advanced surgical assistance and improve computer assisted interventions. In this work, we propose SegMatch, a semi supervised learning method to reduce the need for expensive annotation for laparoscopic and robotic surgical images. SegMatch builds on FixMatch, a widespread semi supervised classification pipeline combining consistency regularization and pseudo labelling, and adapts it for the purpose of segmentation. In our proposed SegMatch, the unlabelled images are weakly augmented and fed into the segmentation model to generate a pseudo-label to enforce the unsupervised loss against the output of the model for the adversarial augmented image on the pixels with a high confidence score. Our adaptation for segmentation tasks includes carefully considering the equivariance and invariance properties of the augmentation functions we rely on. To increase the relevance of our augmentations, we depart from using only handcrafted augmentations and introduce a trainable adversarial augmentation strategy. Our algorithm was evaluated on the MICCAI Instrument Segmentation Challenge datasets Robust-MIS 2019 and EndoVis 2017. Our results demonstrate that adding unlabelled data for training purposes allows us to surpass the performance of fully supervised approaches which are limited by the availability of training data in these challenges. SegMatch also outperforms a range of state-of-the-art semi-supervised learning semantic segmentation models in different labelled to unlabelled data ratios.