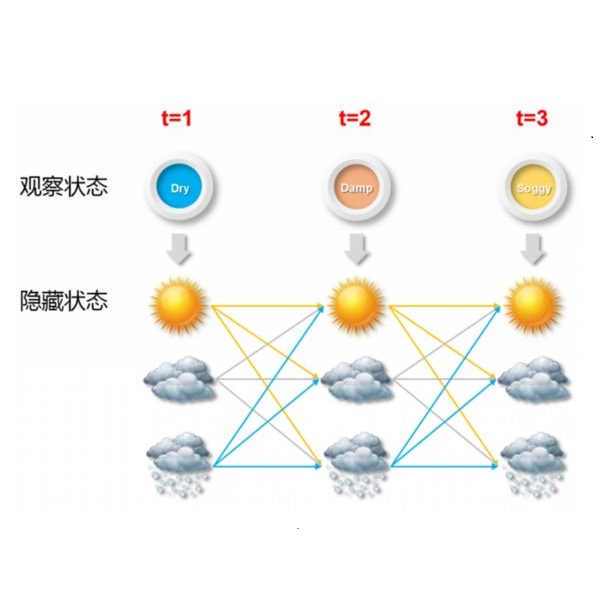
In this paper we consider the problem of quickly detecting changes in hidden Markov models (HMMs) in a Bayesian setting, as well as several structured generalisations including changes in statistically periodic processes, quickest detection of a Markov process across a sensor array, quickest detection of a moving target in a sensor network and quickest change detection (QCD) in multistream data. Our main result establishes an optimal Bayesian HMM QCD rule with a threshold structure. This framework and proof techniques allow us to elegantly establish optimal rules for the structured generalisations by showing that these problems are special cases of the Bayesian HMM QCD problem. The threshold structure enables us to develop bounds to characterise the performance of our optimal rule and provide an efficient method for computing the test statistic. Finally, we examine the performance of our rule in several simulation examples and propose a technique for calculating the optimal threshold.
相關內容
This article proposes omnibus portmanteau tests for contrasting adequacy of time series models. The test statistics are based on combining the autocorrelation function of the conditional residuals, the autocorrelation function of the conditional squared residuals, and the cross-correlation function between these residuals and their squares. The maximum likelihood estimator is used to derive the asymptotic distribution of the proposed test statistics under a general class of time series models, including ARMA, GARCH, and other nonlinear structures. An extensive Monte Carlo simulation study shows that the proposed tests successfully control the type I error probability and tend to have more power than other competitor tests in many scenarios. Two applications to a set of weekly stock returns for 92 companies from the S&P 500 demonstrate the practical use of the proposed tests.
The improvement of pose estimation accuracy is currently the fundamental problem in mobile robots. This study aims to improve the use of observations to enhance accuracy. The selection of feature points affects the accuracy of pose estimation, leading to the question of how the contribution of observation influences the system. Accordingly, the contribution of information to the pose estimation process is analyzed. Moreover, the uncertainty model, sensitivity model, and contribution theory are formulated, providing a method for calculating the contribution of every residual term. The proposed selection method has been theoretically proven capable of achieving a global statistical optimum. The proposed method is tested on artificial data simulations and compared with the KITTI benchmark. The experiments revealed superior results in contrast to ALOAM and MLOAM. The proposed algorithm is implemented in LiDAR odometry and LiDAR Inertial odometry both indoors and outdoors using diverse LiDAR sensors with different scan modes, demonstrating its effectiveness in improving pose estimation accuracy. A new configuration of two laser scan sensors is subsequently inferred. The configuration is valid for three-dimensional pose localization in a prior map and yields results at the centimeter level.
For a partial structural change in a linear regression model with a single break, we develop a continuous record asymptotic framework to build inference methods for the break date. We have T observations with a sampling frequency h over a fixed time horizon [0, N] , and let T with h 0 while keeping the time span N fixed. We impose very mild regularity conditions on an underlying continuous-time model assumed to generate the data. We consider the least-squares estimate of the break date and establish consistency and convergence rate. We provide a limit theory for shrinking magnitudes of shifts and locally increasing variances. The asymptotic distribution corresponds to the location of the extremum of a function of the quadratic variation of the regressors and of a Gaussian centered martingale process over a certain time interval. We can account for the asymmetric informational content provided by the pre- and post-break regimes and show how the location of the break and shift magnitude are key ingredients in shaping the distribution. We consider a feasible version based on plug-in estimates, which provides a very good approximation to the finite sample distribution. We use the concept of Highest Density Region to construct confidence sets. Overall, our method is reliable and delivers accurate coverage probabilities and relatively short average length of the confidence sets. Importantly, it does so irrespective of the size of the break.
Given a graph $G$ of degree $k$ over $n$ vertices, we consider the problem of computing a near maximum cut or a near minimum bisection in polynomial time. For graphs of girth $L$, we develop a local message passing algorithm whose complexity is $O(nkL)$, and that achieves near optimal cut values among all $L$-local algorithms. Focusing on max-cut, the algorithm constructs a cut of value $nk/4+ n\mathsf{P}_\star\sqrt{k/4}+\mathsf{err}(n,k,L)$, where $\mathsf{P}_\star\approx 0.763166$ is the value of the Parisi formula from spin glass theory, and $\mathsf{err}(n,k,L)=o_n(n)+no_k(\sqrt{k})+n \sqrt{k} o_L(1)$ (subscripts indicate the asymptotic variables). Our result generalizes to locally treelike graphs, i.e., graphs whose girth becomes $L$ after removing a small fraction of vertices. Earlier work established that, for random $k$-regular graphs, the typical max-cut value is $nk/4+ n\mathsf{P}_\star\sqrt{k/4}+o_n(n)+no_k(\sqrt{k})$. Therefore our algorithm is nearly optimal on such graphs. An immediate corollary of this result is that random regular graphs have nearly minimum max-cut, and nearly maximum min-bisection among all regular locally treelike graphs. This can be viewed as a combinatorial version of the near-Ramanujan property of random regular graphs.
We consider off-policy evaluation (OPE) in Partially Observable Markov Decision Processes (POMDPs), where the evaluation policy depends only on observable variables and the behavior policy depends on unobservable latent variables. Existing works either assume no unmeasured confounders, or focus on settings where both the observation and the state spaces are tabular. As such, these methods suffer from either a large bias in the presence of unmeasured confounders, or a large variance in settings with continuous or large observation/state spaces. In this work, we first propose novel identification methods for OPE in POMDPs with latent confounders, by introducing bridge functions that link the target policy's value and the observed data distribution. In fully-observable MDPs, these bridge functions reduce to the familiar value functions and marginal density ratios between the evaluation and the behavior policies. We next propose minimax estimation methods for learning these bridge functions. Our proposal permits general function approximation and is thus applicable to settings with continuous or large observation/state spaces. Finally, we construct three estimators based on these estimated bridge functions, corresponding to a value function-based estimator, a marginalized importance sampling estimator, and a doubly-robust estimator. Their nonasymptotic and asymptotic properties are investigated in detail.
We study the problem of list-decodable mean estimation, where an adversary can corrupt a majority of the dataset. Specifically, we are given a set $T$ of $n$ points in $\mathbb{R}^d$ and a parameter $0< \alpha <\frac 1 2$ such that an $\alpha$-fraction of the points in $T$ are i.i.d. samples from a well-behaved distribution $\mathcal{D}$ and the remaining $(1-\alpha)$-fraction are arbitrary. The goal is to output a small list of vectors, at least one of which is close to the mean of $\mathcal{D}$. We develop new algorithms for list-decodable mean estimation, achieving nearly-optimal statistical guarantees, with running time $O(n^{1 + \epsilon_0} d)$, for any fixed $\epsilon_0 > 0$. All prior algorithms for this problem had additional polynomial factors in $\frac 1 \alpha$. We leverage this result, together with additional techniques, to obtain the first almost-linear time algorithms for clustering mixtures of $k$ separated well-behaved distributions, nearly-matching the statistical guarantees of spectral methods. Prior clustering algorithms inherently relied on an application of $k$-PCA, thereby incurring runtimes of $\Omega(n d k)$. This marks the first runtime improvement for this basic statistical problem in nearly two decades. The starting point of our approach is a novel and simpler near-linear time robust mean estimation algorithm in the $\alpha \to 1$ regime, based on a one-shot matrix multiplicative weights-inspired potential decrease. We crucially leverage this new algorithmic framework in the context of the iterative multi-filtering technique of Diakonikolas et al. '18, '20, providing a method to simultaneously cluster and downsample points using one-dimensional projections -- thus, bypassing the $k$-PCA subroutines required by prior algorithms.
In this paper, we propose a time-series stochastic model based on a scale mixture distribution with Markov transitions to detect epileptic seizures in electroencephalography (EEG). In the proposed model, an EEG signal at each time point is assumed to be a random variable following a Gaussian distribution. The covariance matrix of the Gaussian distribution is weighted with a latent scale parameter, which is also a random variable, resulting in the stochastic fluctuations of covariances. By introducing a latent state variable with a Markov chain in the background of this stochastic relationship, time-series changes in the distribution of latent scale parameters can be represented according to the state of epileptic seizures. In an experiment, we evaluated the performance of the proposed model for seizure detection using EEGs with multiple frequency bands decomposed from a clinical dataset. The results demonstrated that the proposed model can detect seizures with high sensitivity and outperformed several baselines.
There is growing interest in object detection in advanced driver assistance systems and autonomous robots and vehicles. To enable such innovative systems, we need faster object detection. In this work, we investigate the trade-off between accuracy and speed with domain-specific approximations, i.e. category-aware image size scaling and proposals scaling, for two state-of-the-art deep learning-based object detection meta-architectures. We study the effectiveness of applying approximation both statically and dynamically to understand the potential and the applicability of them. By conducting experiments on the ImageNet VID dataset, we show that domain-specific approximation has great potential to improve the speed of the system without deteriorating the accuracy of object detectors, i.e. up to 7.5x speedup for dynamic domain-specific approximation. To this end, we present our insights toward harvesting domain-specific approximation as well as devise a proof-of-concept runtime, AutoFocus, that exploits dynamic domain-specific approximation.
Dynamic topic models (DTMs) model the evolution of prevalent themes in literature, online media, and other forms of text over time. DTMs assume that word co-occurrence statistics change continuously and therefore impose continuous stochastic process priors on their model parameters. These dynamical priors make inference much harder than in regular topic models, and also limit scalability. In this paper, we present several new results around DTMs. First, we extend the class of tractable priors from Wiener processes to the generic class of Gaussian processes (GPs). This allows us to explore topics that develop smoothly over time, that have a long-term memory or are temporally concentrated (for event detection). Second, we show how to perform scalable approximate inference in these models based on ideas around stochastic variational inference and sparse Gaussian processes. This way we can train a rich family of DTMs to massive data. Our experiments on several large-scale datasets show that our generalized model allows us to find interesting patterns that were not accessible by previous approaches.
We consider the task of learning the parameters of a {\em single} component of a mixture model, for the case when we are given {\em side information} about that component, we call this the "search problem" in mixture models. We would like to solve this with computational and sample complexity lower than solving the overall original problem, where one learns parameters of all components. Our main contributions are the development of a simple but general model for the notion of side information, and a corresponding simple matrix-based algorithm for solving the search problem in this general setting. We then specialize this model and algorithm to four common scenarios: Gaussian mixture models, LDA topic models, subspace clustering, and mixed linear regression. For each one of these we show that if (and only if) the side information is informative, we obtain parameter estimates with greater accuracy, and also improved computation complexity than existing moment based mixture model algorithms (e.g. tensor methods). We also illustrate several natural ways one can obtain such side information, for specific problem instances. Our experiments on real data sets (NY Times, Yelp, BSDS500) further demonstrate the practicality of our algorithms showing significant improvement in runtime and accuracy.