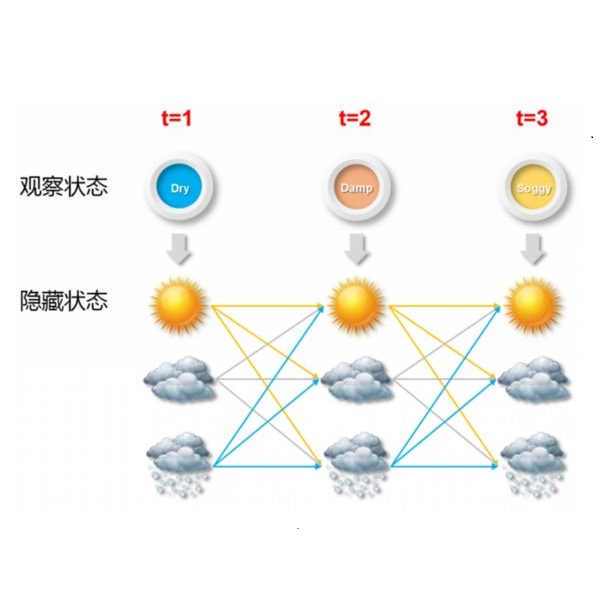
Pufferfish is a Bayesian privacy framework for designing and analyzing privacy mechanisms. It refines differential privacy, the current gold standard in data privacy, by allowing explicit prior knowledge in privacy analysis. Through these privacy frameworks, a number of privacy mechanisms have been developed in literature. In practice, privacy mechanisms often need be modified or adjusted to specific applications. Their privacy risks have to be re-evaluated for different circumstances. Moreover, computing devices only approximate continuous noises through floating-point computation, which is discrete in nature. Privacy proofs can thus be complicated and prone to errors. Such tedious tasks can be burdensome to average data curators. In this paper, we propose an automatic verification technique for Pufferfish privacy. We use hidden Markov models to specify and analyze discretized Pufferfish privacy mechanisms. We show that the Pufferfish verification problem in hidden Markov models is NP-hard. Using Satisfiability Modulo Theories solvers, we propose an algorithm to analyze privacy requirements. We implement our algorithm in a prototypical tool called FAIER, and present several case studies. Surprisingly, our case studies show that na\"ive discretization of well-established privacy mechanisms often fail, witnessed by counterexamples generated by FAIER. In discretized \emph{Above Threshold}, we show that it results in absolutely no privacy. Finally, we compare our approach with testing based approach on several case studies, and show that our verification technique can be combined with testing based approach for the purpose of (i) efficiently certifying counterexamples and (ii) obtaining a better lower bound for the privacy budget $\epsilon$.
相關內容
The exponential growth of collected, processed, and shared microdata has given rise to concerns about individuals' privacy. As a result, laws and regulations have emerged to control what organisations do with microdata and how they protect it. Statistical Disclosure Control seeks to reduce the risk of confidential information disclosure by de-identifying them. Such de-identification is guaranteed through privacy-preserving techniques. However, de-identified data usually results in loss of information, with a possible impact on data analysis precision and model predictive performance. The main goal is to protect the individuals' privacy while maintaining the interpretability of the data, i.e. its usefulness. Statistical Disclosure Control is an area that is expanding and needs to be explored since there is still no solution that guarantees optimal privacy and utility. This survey focuses on all steps of the de-identification process. We present existing privacy-preserving techniques used in microdata de-identification, privacy measures suitable for several disclosure types and, information loss and predictive performance measures. In this survey, we discuss the main challenges raised by privacy constraints, describe the main approaches to handle these obstacles, review taxonomies of privacy-preserving techniques, provide a theoretical analysis of existing comparative studies, and raise multiple open issues.
Markov Chain Monte Carlo (MCMC) is one of the most powerful methods to sample from a given probability distribution, of which the Metropolis Adjusted Langevin Algorithm (MALA) is a variant wherein the gradient of the distribution is used towards faster convergence. However, being set up in the Euclidean framework, MALA might perform poorly in higher dimensional problems or in those involving anisotropic densities as the underlying non-Euclidean aspects of the geometry of the sample space remain unaccounted for. We make use of concepts from differential geometry and stochastic calculus on Riemannian manifolds to geometrically adapt a stochastic differential equation with a non-trivial drift term. This adaptation is also referred to as a stochastic development. We apply this method specifically to the Langevin diffusion equation and arrive at a geometrically adapted Langevin dynamics. This new approach far outperforms MALA, certain manifold variants of MALA, and other approaches such as Hamiltonian Monte Carlo (HMC), its adaptive variant the no-U-turn sampler (NUTS) implemented in Stan, especially as the dimension of the problem increases where often GALA is actually the only successful method. This is evidenced through several numerical examples that include parameter estimation of a broad class of probability distributions and a logistic regression problem.
This document considers the counteracting requirements of privacy and accountability applied to identity management. Based on the requirements of GDPR applied to identity attributes, two forms of identity, with differing balances between privacy and accountability, are suggested, termed "publicly-recognised identity" and "domain-specific identity". These forms of identity can be further refined using "pseudonymisation" and as described in GDPR. This leads to the different forms of identity on the spectrum of accountability vs privacy. It is recommended that the privacy and accountability requirements, and hence the appropriate form of identity, are considered in designing an identification scheme and in the adoption of a scheme by data processing systems. Also, users should be aware of the implications of the form of identity requested by a system, so that they can decide whether this is acceptable.
Pufferfish privacy achieves $\epsilon$-indistinguishability over a set of secret pairs in the disclosed dataset. This paper studies how to attain pufferfish privacy by the exponential mechanism, an additive noise scheme that generalizes Gaussian and Laplace noise. A sufficient condition is derived showing that pufferfish privacy is attained by calibrating noise to the sensitivity of the Kantorovich optimal transport plan. Such a plan can be directly computed by using the data statistics conditioned on the secret, the prior knowledge about the system. It is shown that Gaussian noise provides better data utility than Laplace noise when the privacy budget $\epsilon$ is small. The sufficient condition is then relaxed to reduce the noise power. Experimental results show that the relaxed sufficient condition improves data utility of the pufferfish private data regulation schemes.
The availability of genomic data is essential to progress in biomedical research, personalized medicine, etc. However, its extreme sensitivity makes it problematic, if not outright impossible, to publish or share it. As a result, several initiatives have been launched to experiment with synthetic genomic data, e.g., using generative models to learn the underlying distribution of the real data and generate artificial datasets that preserve its salient characteristics without exposing it. This paper provides the first evaluation of both utility and privacy protection of six state-of-the-art models for generating synthetic genomic data. We assess the performance of the synthetic data on several common tasks, such as allele population statistics and linkage disequilibrium. We then measure privacy through the lens of membership inference attacks, i.e., inferring whether a record was part of the training data. Our experiments show that no single approach to generate synthetic genomic data yields both high utility and strong privacy across the board. Also, the size and nature of the training dataset matter. Moreover, while some combinations of datasets and models produce synthetic data with distributions close to the real data, there often are target data points that are vulnerable to membership inference. Looking forward, our techniques can be used by practitioners to assess the risks of deploying synthetic genomic data in the wild and serve as a benchmark for future work.
This document considers the counteracting requirements of privacy and accountability applied to identity management. Based on the requirements of GDPR 1 applied to identity attributes two forms of identity, with differing balances between privacy and accountability, are suggested termed "publicly-recognised identity" and "domain-specific identity". These forms of identity can be further refined using "pseudonymisation" and as described in GDPR. This leads to the different forms of identity on the spectrum of accountability vs privacy. It is recommended that the privacy and accountability requirements, and hence the appropriate form of identity, is considered in designing an identification scheme, and in the adoption of a scheme by data processing systems. Also, users should be aware of the implications of the form of identity requested by a system so that they can decide whether this is acceptable.
(Gradient) Expectation Maximization (EM) is a widely used algorithm for estimating the maximum likelihood of mixture models or incomplete data problems. A major challenge facing this popular technique is how to effectively preserve the privacy of sensitive data. Previous research on this problem has already lead to the discovery of some Differentially Private (DP) algorithms for (Gradient) EM. However, unlike in the non-private case, existing techniques are not yet able to provide finite sample statistical guarantees. To address this issue, we propose in this paper the first DP version of (Gradient) EM algorithm with statistical guarantees. Moreover, we apply our general framework to three canonical models: Gaussian Mixture Model (GMM), Mixture of Regressions Model (MRM) and Linear Regression with Missing Covariates (RMC). Specifically, for GMM in the DP model, our estimation error is near optimal in some cases. For the other two models, we provide the first finite sample statistical guarantees. Our theory is supported by thorough numerical experiments.
Alternating Direction Method of Multipliers (ADMM) is a widely used tool for machine learning in distributed settings, where a machine learning model is trained over distributed data sources through an interactive process of local computation and message passing. Such an iterative process could cause privacy concerns of data owners. The goal of this paper is to provide differential privacy for ADMM-based distributed machine learning. Prior approaches on differentially private ADMM exhibit low utility under high privacy guarantee and often assume the objective functions of the learning problems to be smooth and strongly convex. To address these concerns, we propose a novel differentially private ADMM-based distributed learning algorithm called DP-ADMM, which combines an approximate augmented Lagrangian function with time-varying Gaussian noise addition in the iterative process to achieve higher utility for general objective functions under the same differential privacy guarantee. We also apply the moments accountant method to bound the end-to-end privacy loss. The theoretical analysis shows that DP-ADMM can be applied to a wider class of distributed learning problems, is provably convergent, and offers an explicit utility-privacy tradeoff. To our knowledge, this is the first paper to provide explicit convergence and utility properties for differentially private ADMM-based distributed learning algorithms. The evaluation results demonstrate that our approach can achieve good convergence and model accuracy under high end-to-end differential privacy guarantee.
The concept of Fisher information can be useful even in cases where the probability distributions of interest are not absolutely continuous with respect to the natural reference measure on the underlying space. Practical examples where this extension is useful are provided in the context of multi-object tracking statistical models. Upon defining the Fisher information without introducing a reference measure, we provide remarkably concise proofs of the loss of Fisher information in some widely used multi-object tracking observation models.
We consider the task of learning the parameters of a {\em single} component of a mixture model, for the case when we are given {\em side information} about that component, we call this the "search problem" in mixture models. We would like to solve this with computational and sample complexity lower than solving the overall original problem, where one learns parameters of all components. Our main contributions are the development of a simple but general model for the notion of side information, and a corresponding simple matrix-based algorithm for solving the search problem in this general setting. We then specialize this model and algorithm to four common scenarios: Gaussian mixture models, LDA topic models, subspace clustering, and mixed linear regression. For each one of these we show that if (and only if) the side information is informative, we obtain parameter estimates with greater accuracy, and also improved computation complexity than existing moment based mixture model algorithms (e.g. tensor methods). We also illustrate several natural ways one can obtain such side information, for specific problem instances. Our experiments on real data sets (NY Times, Yelp, BSDS500) further demonstrate the practicality of our algorithms showing significant improvement in runtime and accuracy.