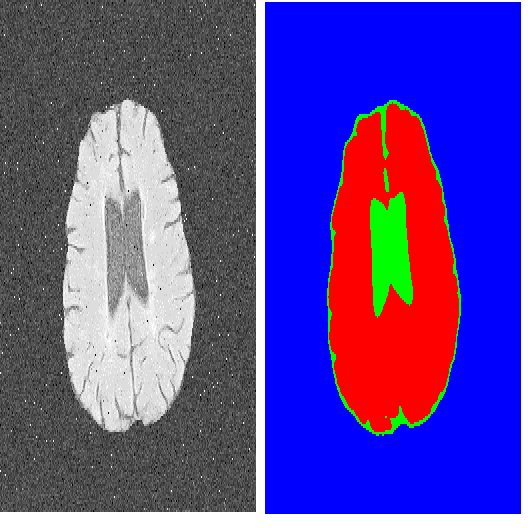
Minimum distance estimation methodology based on an empirical distribution function has been popular due to its desirable properties including robustness. Even though the statistical literature is awash with the research on the minimum distance estimation, the most of it is confined to the theoretical findings: only few statisticians conducted research on the application of the method to real world problems. Through this paper, we extend the domain of application of this methodology to various applied fields by providing a solution to a rather challenging and complicated computational problem. The problem this paper tackles is an image segmentation which has been used in various fields. We propose a novel method based on the classical minimum distance estimation theory to solve the image segmentation problem. The performance of the proposed method is then further elevated by integrating it with the ``segmenting-together" strategy. We demonstrate that the proposed method combined with the segmenting-together strategy successfully completes the segmentation problem when it is applied to the complex, real images such as magnetic resonance images.
相關內容
Recovering temporal image sequences (videos) based on indirect, noisy, or incomplete data is an essential yet challenging task. We specifically consider the case where each data set is missing vital information, which prevents the accurate recovery of the individual images. Although some recent (variational) methods have demonstrated high-resolution image recovery based on jointly recovering sequential images, there remain robustness issues due to parameter tuning and restrictions on the type of the sequential images. Here, we present a method based on hierarchical Bayesian learning for the joint recovery of sequential images that incorporates prior intra- and inter-image information. Our method restores the missing information in each image by "borrowing" it from the other images. As a result, \emph{all} of the individual reconstructions yield improved accuracy. Our method can be used for various data acquisitions and allows for uncertainty quantification. Some preliminary results indicate its potential use for sequential deblurring and magnetic resonance imaging.
The study of robustness has received much attention due to its inevitability in data-driven settings where many systems face uncertainty. One such example of concern is Bayesian Optimization (BO), where uncertainty is multi-faceted, yet there only exists a limited number of works dedicated to this direction. In particular, there is the work of Kirschner et al. (2020), which bridges the existing literature of Distributionally Robust Optimization (DRO) by casting the BO problem from the lens of DRO. While this work is pioneering, it admittedly suffers from various practical shortcomings such as finite contexts assumptions, leaving behind the main question Can one devise a computationally tractable algorithm for solving this DRO-BO problem? In this work, we tackle this question to a large degree of generality by considering robustness against data-shift in $\phi$-divergences, which subsumes many popular choices, such as the $\chi^2$-divergence, Total Variation, and the extant Kullback-Leibler (KL) divergence. We show that the DRO-BO problem in this setting is equivalent to a finite-dimensional optimization problem which, even in the continuous context setting, can be easily implemented with provable sublinear regret bounds. We then show experimentally that our method surpasses existing methods, attesting to the theoretical results.
We study the voting game with information uncertainty where agents can coordinate in groups. We show that strategic voting behaviors have a positive impact on leading to the ``correct'' decision, outperforming the common non-strategic behavior of informative voting and sincere voting. Our results give merit to strategic voting for making good decisions. We reveal the surprising equivalence between a strategy profile being a strong equilibrium and leading to the decision favored by the majority (the {\em informed majority decision}): as the size of the vote goes to infinity, every $\varepsilon$-strong Bayes Nash Equilibrium with $\varepsilon$ converging to $0$ formed by strategic agents leads to the informed majority decision with probability converging to $1$. On the other hand, we show that informative voting leads to the informed majority decision only under unbiased instances, and sincere voting leads to the informed majority decision only when it also forms an equilibrium. In our model, voters' preferences between two alternatives depend on a discrete state variable that is not directly observable. Each voter receives a private signal that is correlated with the state variable.
This paper focuses on a challenging class of inverse problems that is often encountered in applications. The forward model is a complex non-linear black-box, potentially non-injective, whose outputs cover multiple decades in amplitude. Observations are supposed to be simultaneously damaged by additive and multiplicative noises and censorship. As needed in many applications, the aim of this work is to provide uncertainty quantification on top of parameter estimates. The resulting log-likelihood is intractable and potentially non-log-concave. An adapted Bayesian approach is proposed to provide credibility intervals along with point estimates. An MCMC algorithm is proposed to deal with the multimodal posterior distribution, even in a situation where there is no global Lipschitz constant (or it is very large). It combines two kernels, namely an improved version of (Preconditioned Metropolis Adjusted Langevin) PMALA and a Multiple Try Metropolis (MTM) kernel. Whenever smooth, its gradient admits a Lipschitz constant too large to be exploited in the inference process. This sampler addresses all the challenges induced by the complex form of the likelihood. The proposed method is illustrated on classical test multimodal distributions as well as on a challenging and realistic inverse problem in astronomy.
This paper presents a new method for reconstructing regions of interest (ROI) from a limited number of computed tomography (CT) measurements. Classical model-based iterative reconstruction methods lead to images with predictable features. Still, they often suffer from tedious parameterization and slow convergence. On the contrary, deep learning methods are fast, and they can reach high reconstruction quality by leveraging information from large datasets, but they lack interpretability. At the crossroads of both methods, deep unfolding networks have been recently proposed. Their design includes the physics of the imaging system and the steps of an iterative optimization algorithm. Motivated by the success of these networks for various applications, we introduce an unfolding neural network called U-RDBFB designed for ROI CT reconstruction from limited data. Few-view truncated data are effectively handled thanks to a robust non-convex data fidelity term combined with a sparsity-inducing regularization function. We unfold the Dual Block coordinate Forward-Backward (DBFB) algorithm, embedded in an iterative reweighted scheme, allowing the learning of key parameters in a supervised manner. Our experiments show an improvement over several state-of-the-art methods, including a model-based iterative scheme, a multi-scale deep learning architecture, and other deep unfolding methods.
We propose a simple, statistically principled, and theoretically justified method to improve supervised learning when the training set is not representative, a situation known as covariate shift. We build upon a well-established methodology in causal inference, and show that the effects of covariate shift can be reduced or eliminated by conditioning on propensity scores. In practice, this is achieved by fitting learners within strata constructed by partitioning the data based on the estimated propensity scores, leading to approximately balanced covariates and much-improved target prediction. We demonstrate the effectiveness of our general-purpose method on two contemporary research questions in cosmology, outperforming state-of-the-art importance weighting methods. We obtain the best reported AUC (0.958) on the updated "Supernovae photometric classification challenge", and we improve upon existing conditional density estimation of galaxy redshift from Sloan Data Sky Survey (SDSS) data.
Integrated visible light positioning and communication (VLPC), capable of combining advantages of visible light communications (VLC) and visible light positioning (VLP), is a promising key technology for the future Internet of Things. In VLPC networks, positioning and communications are inherently coupled, which has not been sufficiently explored in the literature. We propose a robust power allocation scheme for integrated VLPC Networks by exploiting the intrinsic relationship between positioning and communications. Specifically, we derive explicit relationships between random positioning errors, following both a Gaussian distribution and an arbitrary distribution, and channel state information errors. Then, we minimize the Cramer-Rao lower bound (CRLB) of positioning errors, subject to the rate outage constraint and the power constraints, which is a chance-constrained optimization problem and generally computationally intractable. To circumvent the nonconvex challenge, we conservatively transform the chance constraints to deterministic forms by using the Bernstein-type inequality and the conditional value-at-risk for the Gaussian and arbitrary distributed positioning errors, respectively, and then approximate them as convex semidefinite programs. Finally, simulation results verify the robustness and effectiveness of our proposed integrated VLPC design schemes.
Deep Learning algorithms have achieved the state-of-the-art performance for Image Classification and have been used even in security-critical applications, such as biometric recognition systems and self-driving cars. However, recent works have shown those algorithms, which can even surpass the human capabilities, are vulnerable to adversarial examples. In Computer Vision, adversarial examples are images containing subtle perturbations generated by malicious optimization algorithms in order to fool classifiers. As an attempt to mitigate these vulnerabilities, numerous countermeasures have been constantly proposed in literature. Nevertheless, devising an efficient defense mechanism has proven to be a difficult task, since many approaches have already shown to be ineffective to adaptive attackers. Thus, this self-containing paper aims to provide all readerships with a review of the latest research progress on Adversarial Machine Learning in Image Classification, however with a defender's perspective. Here, novel taxonomies for categorizing adversarial attacks and defenses are introduced and discussions about the existence of adversarial examples are provided. Further, in contrast to exisiting surveys, it is also given relevant guidance that should be taken into consideration by researchers when devising and evaluating defenses. Finally, based on the reviewed literature, it is discussed some promising paths for future research.
Deep neural networks (DNNs) are successful in many computer vision tasks. However, the most accurate DNNs require millions of parameters and operations, making them energy, computation and memory intensive. This impedes the deployment of large DNNs in low-power devices with limited compute resources. Recent research improves DNN models by reducing the memory requirement, energy consumption, and number of operations without significantly decreasing the accuracy. This paper surveys the progress of low-power deep learning and computer vision, specifically in regards to inference, and discusses the methods for compacting and accelerating DNN models. The techniques can be divided into four major categories: (1) parameter quantization and pruning, (2) compressed convolutional filters and matrix factorization, (3) network architecture search, and (4) knowledge distillation. We analyze the accuracy, advantages, disadvantages, and potential solutions to the problems with the techniques in each category. We also discuss new evaluation metrics as a guideline for future research.

Recent advances in 3D fully convolutional networks (FCN) have made it feasible to produce dense voxel-wise predictions of volumetric images. In this work, we show that a multi-class 3D FCN trained on manually labeled CT scans of several anatomical structures (ranging from the large organs to thin vessels) can achieve competitive segmentation results, while avoiding the need for handcrafting features or training class-specific models. To this end, we propose a two-stage, coarse-to-fine approach that will first use a 3D FCN to roughly define a candidate region, which will then be used as input to a second 3D FCN. This reduces the number of voxels the second FCN has to classify to ~10% and allows it to focus on more detailed segmentation of the organs and vessels. We utilize training and validation sets consisting of 331 clinical CT images and test our models on a completely unseen data collection acquired at a different hospital that includes 150 CT scans, targeting three anatomical organs (liver, spleen, and pancreas). In challenging organs such as the pancreas, our cascaded approach improves the mean Dice score from 68.5 to 82.2%, achieving the highest reported average score on this dataset. We compare with a 2D FCN method on a separate dataset of 240 CT scans with 18 classes and achieve a significantly higher performance in small organs and vessels. Furthermore, we explore fine-tuning our models to different datasets. Our experiments illustrate the promise and robustness of current 3D FCN based semantic segmentation of medical images, achieving state-of-the-art results. Our code and trained models are available for download: //github.com/holgerroth/3Dunet_abdomen_cascade.