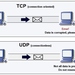
Batched network coding (BNC) is a solution to multi-hop transmission on networks with packet loss. To be compatible with the existing infrastructure, BNC is usually implemented over UDP. A single error bit will probably result in discarding the packet. UDP-Lite is a variant of UDP that supports partial checksums. As long as the data covered by the checksum is correct, damaged payload will be delivered. With UDP-Lite, we can cope with other techniques such as payload aggregation of BNC packets to reduce the protocol overhead, and forward error correction to combat against bit errors. Unlike traditional transmissions, BNC has a loss resilience feature and there are dependencies between BNC packets. In this paper, we conduct a preliminary investigation on BNC over UDP-Lite. We show that aggregating as much as we can is not always the best strategy, and a hop-by-hop distributed efficiency optimization approach may lead to a worse throughput compared with the scheme without aggregation in a long network. These unnatural results caution that a casual integration of techniques with BNC can be harmful, and give us hints on future research directions.
相關內容
A key goal in mechanistic interpretability is circuit analysis: finding sparse subgraphs of models corresponding to specific behaviors or capabilities. However, MLP sublayers make fine-grained circuit analysis on transformer-based language models difficult. In particular, interpretable features -- such as those found by sparse autoencoders (SAEs) -- are typically linear combinations of extremely many neurons, each with its own nonlinearity to account for. Circuit analysis in this setting thus either yields intractably large circuits or fails to disentangle local and global behavior. To address this we explore transcoders, which seek to faithfully approximate a densely activating MLP layer with a wider, sparsely-activating MLP layer. We introduce a novel method for using transcoders to perform weights-based circuit analysis through MLP sublayers. The resulting circuits neatly factorize into input-dependent and input-invariant terms. We then successfully train transcoders on language models with 120M, 410M, and 1.4B parameters, and find them to perform at least on par with SAEs in terms of sparsity, faithfulness, and human-interpretability. Finally, we apply transcoders to reverse-engineer unknown circuits in the model, and we obtain novel insights regarding the "greater-than circuit" in GPT2-small. Our results suggest that transcoders can prove effective in decomposing model computations involving MLPs into interpretable circuits. Code is available at //github.com/jacobdunefsky/transcoder_circuits/.
The application of deep neural networks in geospatial data has become a trending research problem in the present day. A significant amount of statistical research has already been introduced, such as generalized least square optimization by incorporating spatial variance-covariance matrix, considering basis functions in the input nodes of the neural networks, and so on. However, for lattice data, there is no available literature about the utilization of asymptotic analysis of neural networks in regression for spatial data. This article proposes a consistent localized two-layer deep neural network-based regression for spatial data. We have proved the consistency of this deep neural network for bounded and unbounded spatial domains under a fixed sampling design of mixed-increasing spatial regions. We have proved that its asymptotic convergence rate is faster than that of \cite{zhan2024neural}'s neural network and an improved generalization of \cite{shen2023asymptotic}'s neural network structure. We empirically observe the rate of convergence of discrepancy measures between the empirical probability distribution of observed and predicted data, which will become faster for a less smooth spatial surface. We have applied our asymptotic analysis of deep neural networks to the estimation of the monthly average temperature of major cities in the USA from its satellite image. This application is an effective showcase of non-linear spatial regression. We demonstrate our methodology with simulated lattice data in various scenarios.
With the advancements in graph neural network, there has been increasing interest in applying this network to ECG signal analysis. In this study, we generated an adjacency matrix using correlation matrix of extracted features and applied a graph neural network to classify arrhythmias. The proposed model was compared with existing approaches from the literature. The results demonstrated that precision and recall for all arrhythmia classes exceeded 50%, suggesting that this method can be considered an approach for arrhythmia classification.
The Schr\"odinger Bridge (SB) problem offers a powerful framework for combining optimal transport and diffusion models. A promising recent approach to solve the SB problem is the Iterative Markovian Fitting (IMF) procedure, which alternates between Markovian and reciprocal projections of continuous-time stochastic processes. However, the model built by the IMF procedure has a long inference time due to using many steps of numerical solvers for stochastic differential equations. To address this limitation, we propose a novel Discrete-time IMF (D-IMF) procedure in which learning of stochastic processes is replaced by learning just a few transition probabilities in discrete time. Its great advantage is that in practice it can be naturally implemented using the Denoising Diffusion GAN (DD-GAN), an already well-established adversarial generative modeling technique. We show that our D-IMF procedure can provide the same quality of unpaired domain translation as the IMF, using only several generation steps instead of hundreds. We provide the code at //github.com/Daniil-Selikhanovych/ASBM.

Technology ecosystems often undergo significant transformations as they mature. For example, telephony, the Internet, and PCs all started with a single provider, but in the United States each is now served by a competitive market that uses comprehensive and universal technology standards to provide compatibility. This white paper presents our view on how the cloud ecosystem, barely over fifteen years old, could evolve as it matures.
Recently, a considerable literature has grown up around the theme of Graph Convolutional Network (GCN). How to effectively leverage the rich structural information in complex graphs, such as knowledge graphs with heterogeneous types of entities and relations, is a primary open challenge in the field. Most GCN methods are either restricted to graphs with a homogeneous type of edges (e.g., citation links only), or focusing on representation learning for nodes only instead of jointly propagating and updating the embeddings of both nodes and edges for target-driven objectives. This paper addresses these limitations by proposing a novel framework, namely the Knowledge Embedding based Graph Convolutional Network (KE-GCN), which combines the power of GCNs in graph-based belief propagation and the strengths of advanced knowledge embedding (a.k.a. knowledge graph embedding) methods, and goes beyond. Our theoretical analysis shows that KE-GCN offers an elegant unification of several well-known GCN methods as specific cases, with a new perspective of graph convolution. Experimental results on benchmark datasets show the advantageous performance of KE-GCN over strong baseline methods in the tasks of knowledge graph alignment and entity classification.
Minimizing cross-entropy over the softmax scores of a linear map composed with a high-capacity encoder is arguably the most popular choice for training neural networks on supervised learning tasks. However, recent works show that one can directly optimize the encoder instead, to obtain equally (or even more) discriminative representations via a supervised variant of a contrastive objective. In this work, we address the question whether there are fundamental differences in the sought-for representation geometry in the output space of the encoder at minimal loss. Specifically, we prove, under mild assumptions, that both losses attain their minimum once the representations of each class collapse to the vertices of a regular simplex, inscribed in a hypersphere. We provide empirical evidence that this configuration is attained in practice and that reaching a close-to-optimal state typically indicates good generalization performance. Yet, the two losses show remarkably different optimization behavior. The number of iterations required to perfectly fit to data scales superlinearly with the amount of randomly flipped labels for the supervised contrastive loss. This is in contrast to the approximately linear scaling previously reported for networks trained with cross-entropy.
This paper presents a new approach for assembling graph neural networks based on framelet transforms. The latter provides a multi-scale representation for graph-structured data. With the framelet system, we can decompose the graph feature into low-pass and high-pass frequencies as extracted features for network training, which then defines a framelet-based graph convolution. The framelet decomposition naturally induces a graph pooling strategy by aggregating the graph feature into low-pass and high-pass spectra, which considers both the feature values and geometry of the graph data and conserves the total information. The graph neural networks with the proposed framelet convolution and pooling achieve state-of-the-art performance in many types of node and graph prediction tasks. Moreover, we propose shrinkage as a new activation for the framelet convolution, which thresholds the high-frequency information at different scales. Compared to ReLU, shrinkage in framelet convolution improves the graph neural network model in terms of denoising and signal compression: noises in both node and structure can be significantly reduced by accurately cutting off the high-pass coefficients from framelet decomposition, and the signal can be compressed to less than half its original size with the prediction performance well preserved.
This paper is an attempt to explain all the matrix calculus you need in order to understand the training of deep neural networks. We assume no math knowledge beyond what you learned in calculus 1, and provide links to help you refresh the necessary math where needed. Note that you do not need to understand this material before you start learning to train and use deep learning in practice; rather, this material is for those who are already familiar with the basics of neural networks, and wish to deepen their understanding of the underlying math. Don't worry if you get stuck at some point along the way---just go back and reread the previous section, and try writing down and working through some examples. And if you're still stuck, we're happy to answer your questions in the Theory category at forums.fast.ai. Note: There is a reference section at the end of the paper summarizing all the key matrix calculus rules and terminology discussed here. See related articles at //explained.ai

This paper proposes a method to modify traditional convolutional neural networks (CNNs) into interpretable CNNs, in order to clarify knowledge representations in high conv-layers of CNNs. In an interpretable CNN, each filter in a high conv-layer represents a certain object part. We do not need any annotations of object parts or textures to supervise the learning process. Instead, the interpretable CNN automatically assigns each filter in a high conv-layer with an object part during the learning process. Our method can be applied to different types of CNNs with different structures. The clear knowledge representation in an interpretable CNN can help people understand the logics inside a CNN, i.e., based on which patterns the CNN makes the decision. Experiments showed that filters in an interpretable CNN were more semantically meaningful than those in traditional CNNs.