亚洲男人的天堂2018av,欧美草比,久久久久久免费视频精选,国色天香在线看免费,久久久久亚洲av成人片仓井空

Machine Learning (ML) techniques are increasingly adopted to tackle ever-evolving high-profile network attacks, including DDoS, botnet, and ransomware, due to their unique ability to extract complex patterns hidden in data streams. These approaches are however routinely validated with data collected in the same environment, and their performance degrades when deployed in different network topologies and/or applied on previously unseen traffic, as we uncover. This suggests malicious/benign behaviors are largely learned superficially and ML-based Network Intrusion Detection System (NIDS) need revisiting, to be effective in practice. In this paper we dive into the mechanics of large-scale network attacks, with a view to understanding how to use ML for Network Intrusion Detection (NID) in a principled way. We reveal that, although cyberattacks vary significantly in terms of payloads, vectors and targets, their early stages, which are critical to successful attack outcomes, share many similarities and exhibit important temporal correlations. Therefore, we treat NID as a time-sensitive task and propose NetSentry, perhaps the first of its kind NIDS that builds on Bidirectional Asymmetric LSTM (Bi-ALSTM), an original ensemble of sequential neural models, to detect network threats before they spread. We cross-evaluate NetSentry using two practical datasets, training on one and testing on the other, and demonstrate F1 score gains above 33% over the state-of-the-art, as well as up to 3 times higher rates of detecting attacks such as XSS and web bruteforce. Further, we put forward a novel data augmentation technique that boosts the generalization abilities of a broad range of supervised deep learning algorithms, leading to average F1 score gains above 35%.

What is the "right" topological invariant of a large point cloud X? Prior research has focused on estimating the full persistence diagram of X, a quantity that is very expensive to compute, unstable to outliers, and far from a sufficient statistic. We therefore propose that the correct invariant is not the persistence diagram of X, but rather the collection of persistence diagrams of many small subsets. This invariant, which we call "distributed persistence," is perfectly parallelizable, more stable to outliers, and has a rich inverse theory. The map from the space of point clouds (with the quasi-isometry metric) to the space of distributed persistence invariants (with the Hausdorff-Bottleneck distance) is a global quasi-isometry. This is a much stronger property than simply being injective, as it implies that the inverse of a small neighborhood is a small neighborhood, and is to our knowledge the only result of its kind in the TDA literature. Moreover, the quasi-isometry bounds depend on the size of the subsets taken, so that as the size of these subsets goes from small to large, the invariant interpolates between a purely geometric one and a topological one. Lastly, we note that our inverse results do not actually require considering all subsets of a fixed size (an enormous collection), but a relatively small collection satisfying certain covering properties that arise with high probability when randomly sampling subsets. These theoretical results are complemented by two synthetic experiments demonstrating the use of distributed persistence in practice.

Deep neural networks have been shown to be very powerful modeling tools for many supervised learning tasks involving complex input patterns. However, they can also easily overfit to training set biases and label noises. In addition to various regularizers, example reweighting algorithms are popular solutions to these problems, but they require careful tuning of additional hyperparameters, such as example mining schedules and regularization hyperparameters. In contrast to past reweighting methods, which typically consist of functions of the cost value of each example, in this work we propose a novel meta-learning algorithm that learns to assign weights to training examples based on their gradient directions. To determine the example weights, our method performs a meta gradient descent step on the current mini-batch example weights (which are initialized from zero) to minimize the loss on a clean unbiased validation set. Our proposed method can be easily implemented on any type of deep network, does not require any additional hyperparameter tuning, and achieves impressive performance on class imbalance and corrupted label problems where only a small amount of clean validation data is available.

Few-shot Learning aims to learn classifiers for new classes with only a few training examples per class. Existing meta-learning or metric-learning based few-shot learning approaches are limited in handling diverse domains with various number of labels. The meta-learning approaches train a meta learner to predict weights of homogeneous-structured task-specific networks, requiring a uniform number of classes across tasks. The metric-learning approaches learn one task-invariant metric for all the tasks, and they fail if the tasks diverge. We propose to deal with these limitations with meta metric learning. Our meta metric learning approach consists of task-specific learners, that exploit metric learning to handle flexible labels, and a meta learner, that discovers good parameters and gradient decent to specify the metrics in task-specific learners. Thus the proposed model is able to handle unbalanced classes as well as to generate task-specific metrics. We test our approach in the `$k$-shot $N$-way' few-shot learning setting used in previous work and new realistic few-shot setting with diverse multi-domain tasks and flexible label numbers. Experiments show that our approach attains superior performances in both settings.

We study object recognition under the constraint that each object class is only represented by very few observations. In such cases, naive supervised learning would lead to severe over-fitting in deep neural networks due to limited training data. We tackle this problem by creating much more training data through label propagation from the few labeled examples to a vast collection of unannotated images. Our main insight is that such a label propagation scheme can be highly effective when the similarity metric used for propagation is learned and transferred from other related domains with lots of data. We test our approach on semi-supervised learning, transfer learning and few-shot recognition, where we learn our similarity metric using various supervised/unsupervised pretraining methods, and transfer it to unlabeled data across different data distributions. By taking advantage of unlabeled data in this way, we achieve significant improvements on all three tasks. Notably, our approach outperforms current state-of-the-art techniques by an absolute $20\%$ for semi-supervised learning on CIFAR10, $10\%$ for transfer learning from ImageNet to CIFAR10, and $6\%$ for few-shot recognition on mini-ImageNet, when labeled examples are limited.

Tracking by detection is a common approach to solving the Multiple Object Tracking problem. In this paper we show how deep metric learning can be used to improve three aspects of tracking by detection. We train a convolutional neural network to learn an embedding function in a Siamese configuration on a large person re-identification dataset offline. It is then used to improve the online performance of tracking while retaining a high frame rate. We use this learned appearance metric to robustly build estimates of pedestrian's trajectories in the MOT16 dataset. In breaking with the tracking by detection model, we use our appearance metric to propose detections using the predicted state of a tracklet as a prior in the case where the detector fails. This method achieves competitive results in evaluation, especially among online, real-time approaches. We present an ablative study showing the impact of each of the three uses of our deep appearance metric.

Metric learning learns a metric function from training data to calculate the similarity or distance between samples. From the perspective of feature learning, metric learning essentially learns a new feature space by feature transformation (e.g., Mahalanobis distance metric). However, traditional metric learning algorithms are shallow, which just learn one metric space (feature transformation). Can we further learn a better metric space from the learnt metric space? In other words, can we learn metric progressively and nonlinearly like deep learning by just using the existing metric learning algorithms? To this end, we present a hierarchical metric learning scheme and implement an online deep metric learning framework, namely ODML. Specifically, we take one online metric learning algorithm as a metric layer, followed by a nonlinear layer (i.e., ReLU), and then stack these layers modelled after the deep learning. The proposed ODML enjoys some nice properties, indeed can learn metric progressively and performs superiorly on some datasets. Various experiments with different settings have been conducted to verify these properties of the proposed ODML.

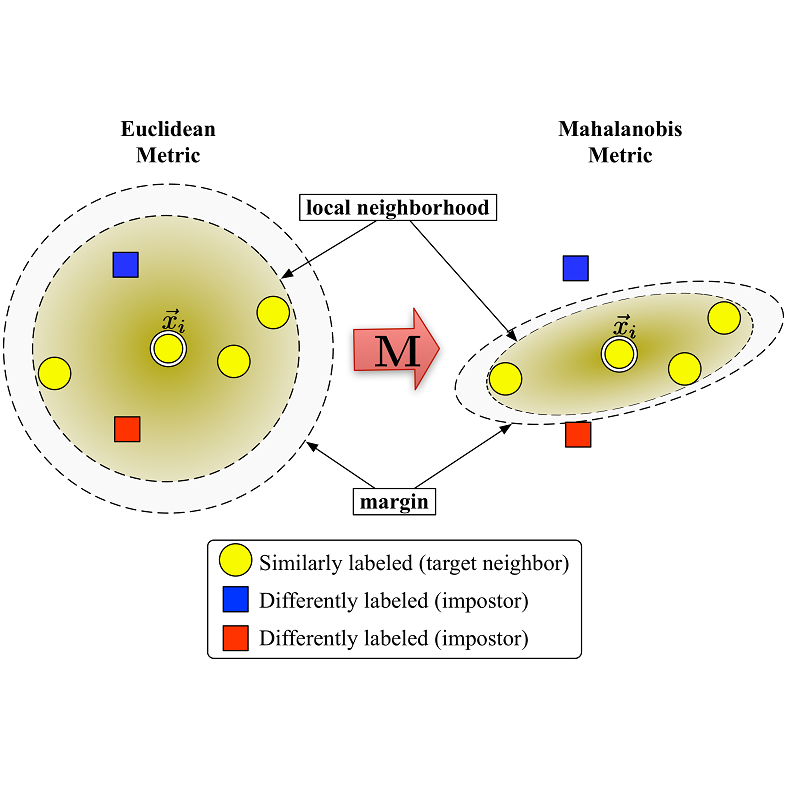
Large margin nearest neighbor (LMNN) is a metric learner which optimizes the performance of the popular $k$NN classifier. However, its resulting metric relies on pre-selected target neighbors. In this paper, we address the feasibility of LMNN's optimization constraints regarding these target points, and introduce a mathematical measure to evaluate the size of the feasible region of the optimization problem. We enhance the optimization framework of LMNN by a weighting scheme which prefers data triplets which yield a larger feasible region. This increases the chances to obtain a good metric as the solution of LMNN's problem. We evaluate the performance of the resulting feasibility-based LMNN algorithm using synthetic and real datasets. The empirical results show an improved accuracy for different types of datasets in comparison to regular LMNN.

In this work we present a novel unsupervised framework for hard training example mining. The only input to the method is a collection of images relevant to the target application and a meaningful initial representation, provided e.g. by pre-trained CNN. Positive examples are distant points on a single manifold, while negative examples are nearby points on different manifolds. Both types of examples are revealed by disagreements between Euclidean and manifold similarities. The discovered examples can be used in training with any discriminative loss. The method is applied to unsupervised fine-tuning of pre-trained networks for fine-grained classification and particular object retrieval. Our models are on par or are outperforming prior models that are fully or partially supervised.

Product recommendation systems are important for major movie studios during the movie greenlight process and as part of machine learning personalization pipelines. Collaborative Filtering (CF) models have proved to be effective at powering recommender systems for online streaming services with explicit customer feedback data. CF models do not perform well in scenarios in which feedback data is not available, in cold start situations like new product launches, and situations with markedly different customer tiers (e.g., high frequency customers vs. casual customers). Generative natural language models that create useful theme-based representations of an underlying corpus of documents can be used to represent new product descriptions, like new movie plots. When combined with CF, they have shown to increase the performance in cold start situations. Outside of those cases though in which explicit customer feedback is available, recommender engines must rely on binary purchase data, which materially degrades performance. Fortunately, purchase data can be combined with product descriptions to generate meaningful representations of products and customer trajectories in a convenient product space in which proximity represents similarity. Learning to measure the distance between points in this space can be accomplished with a deep neural network that trains on customer histories and on dense vectorizations of product descriptions. We developed a system based on Collaborative (Deep) Metric Learning (CML) to predict the purchase probabilities of new theatrical releases. We trained and evaluated the model using a large dataset of customer histories, and tested the model for a set of movies that were released outside of the training window. Initial experiments show gains relative to models that do not train on collaborative preferences.