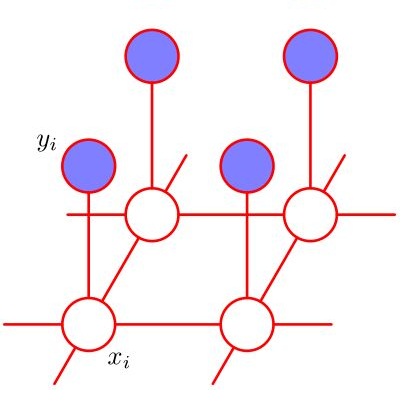
We propose a penalized pseudo-likelihood criterion to estimate the graph of conditional dependencies in a discrete Markov random field that can be partially observed. We prove the convergence of the estimator in the case of a finite or countable infinite set of variables. In the finite case the underlying graph can be recovered with probability one, while in the countable infinite case we can recover any finite sub-graph with probability one, by allowing the candidate neighborhoods to grow with the sample size n and provided the penalizing constant is sufficiently large. Our method requires minimal assumptions on the probability distribution and contrary to other approaches in the literature, the usual positivity condition is not needed. We evaluate the performance of the estimator on simulated data and we apply the methodology to a real dataset of stock index markets in different countries.
相關內容
An irreducible stochastic matrix with rational entries has a stationary distribution given by a vector of rational numbers. We give an upper bound on the lowest common denominator of the entries of this vector. Bounds of this kind are used to study the complexity of algorithms for solving stochastic mean payoff games. They are usually derived using the Hadamard inequality, but this leads to suboptimal results. We replace the Hadamard inequality with the Markov chain tree formula in order to obtain optimal bounds. We also adapt our approach to obtain bounds on the absorption probabilities of finite Markov chains and on the gains and bias vectors of Markov chains with rewards.
We study the fundamental problem of ReLU regression, where the goal is to fit Rectified Linear Units (ReLUs) to data. This supervised learning task is efficiently solvable in the realizable setting, but is known to be computationally hard with adversarial label noise. In this work, we focus on ReLU regression in the Massart noise model, a natural and well-studied semi-random noise model. In this model, the label of every point is generated according to a function in the class, but an adversary is allowed to change this value arbitrarily with some probability, which is {\em at most} $\eta < 1/2$. We develop an efficient algorithm that achieves exact parameter recovery in this model under mild anti-concentration assumptions on the underlying distribution. Such assumptions are necessary for exact recovery to be information-theoretically possible. We demonstrate that our algorithm significantly outperforms naive applications of $\ell_1$ and $\ell_2$ regression on both synthetic and real data.
The tube method or the volume-of-tube method approximates the tail probability of the maximum of a smooth Gaussian random field with zero mean and unit variance. This method evaluates the volume of a spherical tube about the index set, and then transforms it to the tail probability. In this study, we generalize the tube method to a case in which the variance is not constant. We provide the volume formula for a spherical tube with a non-constant radius in terms of curvature tensors, and the tail probability formula of the maximum of a Gaussian random field with inhomogeneous variance, as well as its Laplace approximation. In particular, the critical radius of the tube is generalized for evaluation of the asymptotic approximation error. As an example, we discuss the approximation of the largest eigenvalue distribution of the Wishart matrix with a non-identity matrix parameter. The Bonferroni method is the tube method when the index set is a finite set. We provide the formula for the asymptotic approximation error for the Bonferroni method when the variance is not constant.
Estimating the density of a continuous random variable X has been studied extensively in statistics, in the setting where n independent observations of X are given a priori and one wishes to estimate the density from that. Popular methods include histograms and kernel density estimators. In this review paper, we are interested instead in the situation where the observations are generated by Monte Carlo simulation from a model. Then, one can take advantage of variance reduction methods such as stratification, conditional Monte Carlo, and randomized quasi-Monte Carlo (RQMC), and obtain a more accurate density estimator than with standard Monte Carlo for a given computing budget. We discuss several ways of doing this, proposed in recent papers, with a focus on methods that exploit RQMC. A first idea is to directly combine RQMC with a standard kernel density estimator. Another one is to adapt a simulation-based derivative estimation method such as smoothed perturbation analysis or the likelihood ratio method to obtain a continuous estimator of the cdf, whose derivative is an unbiased estimator of the density. This can then be combined with RQMC. We summarize recent theoretical results with these approaches and give numerical illustrations of how they improve the convergence of the mean square integrated error.
This paper studies the rates of convergence for learning distributions implicitly with the adversarial framework and Generative Adversarial Networks (GANs), which subsume Wasserstein, Sobolev, MMD GAN, and Generalized/Simulated Method of Moments (GMM/SMM) as special cases. We study a wide range of parametric and nonparametric target distributions under a host of objective evaluation metrics. We investigate how to obtain valid statistical guarantees for GANs through the lens of regularization. On the nonparametric end, we derive the optimal minimax rates for distribution estimation under the adversarial framework. On the parametric end, we establish a theory for general neural network classes (including deep leaky ReLU networks) that characterizes the interplay on the choice of generator and discriminator pair. We discover and isolate a new notion of regularization, called the generator-discriminator-pair regularization, that sheds light on the advantage of GANs compared to classical parametric and nonparametric approaches for explicit distribution estimation. We develop novel oracle inequalities as the main technical tools for analyzing GANs, which are of independent interest.
Graph neural networks (GNNs) are a popular class of machine learning models whose major advantage is their ability to incorporate a sparse and discrete dependency structure between data points. Unfortunately, GNNs can only be used when such a graph-structure is available. In practice, however, real-world graphs are often noisy and incomplete or might not be available at all. With this work, we propose to jointly learn the graph structure and the parameters of graph convolutional networks (GCNs) by approximately solving a bilevel program that learns a discrete probability distribution on the edges of the graph. This allows one to apply GCNs not only in scenarios where the given graph is incomplete or corrupted but also in those where a graph is not available. We conduct a series of experiments that analyze the behavior of the proposed method and demonstrate that it outperforms related methods by a significant margin.
This paper proposes a model-free Reinforcement Learning (RL) algorithm to synthesise policies for an unknown Markov Decision Process (MDP), such that a linear time property is satisfied. We convert the given property into a Limit Deterministic Buchi Automaton (LDBA), then construct a synchronized MDP between the automaton and the original MDP. According to the resulting LDBA, a reward function is then defined over the state-action pairs of the product MDP. With this reward function, our algorithm synthesises a policy whose traces satisfies the linear time property: as such, the policy synthesis procedure is "constrained" by the given specification. Additionally, we show that the RL procedure sets up an online value iteration method to calculate the maximum probability of satisfying the given property, at any given state of the MDP - a convergence proof for the procedure is provided. Finally, the performance of the algorithm is evaluated via a set of numerical examples. We observe an improvement of one order of magnitude in the number of iterations required for the synthesis compared to existing approaches.
In structure learning, the output is generally a structure that is used as supervision information to achieve good performance. Considering the interpretation of deep learning models has raised extended attention these years, it will be beneficial if we can learn an interpretable structure from deep learning models. In this paper, we focus on Recurrent Neural Networks (RNNs) whose inner mechanism is still not clearly understood. We find that Finite State Automaton (FSA) that processes sequential data has more interpretable inner mechanism and can be learned from RNNs as the interpretable structure. We propose two methods to learn FSA from RNN based on two different clustering methods. We first give the graphical illustration of FSA for human beings to follow, which shows the interpretability. From the FSA's point of view, we then analyze how the performance of RNNs are affected by the number of gates, as well as the semantic meaning behind the transition of numerical hidden states. Our results suggest that RNNs with simple gated structure such as Minimal Gated Unit (MGU) is more desirable and the transitions in FSA leading to specific classification result are associated with corresponding words which are understandable by human beings.
We consider the exploration-exploitation trade-off in reinforcement learning and we show that an agent imbued with a risk-seeking utility function is able to explore efficiently, as measured by regret. The parameter that controls how risk-seeking the agent is can be optimized exactly, or annealed according to a schedule. We call the resulting algorithm K-learning and show that the corresponding K-values are optimistic for the expected Q-values at each state-action pair. The K-values induce a natural Boltzmann exploration policy for which the `temperature' parameter is equal to the risk-seeking parameter. This policy achieves an expected regret bound of $\tilde O(L^{3/2} \sqrt{S A T})$, where $L$ is the time horizon, $S$ is the number of states, $A$ is the number of actions, and $T$ is the total number of elapsed time-steps. This bound is only a factor of $L$ larger than the established lower bound. K-learning can be interpreted as mirror descent in the policy space, and it is similar to other well-known methods in the literature, including Q-learning, soft-Q-learning, and maximum entropy policy gradient, and is closely related to optimism and count based exploration methods. K-learning is simple to implement, as it only requires adding a bonus to the reward at each state-action and then solving a Bellman equation. We conclude with a numerical example demonstrating that K-learning is competitive with other state-of-the-art algorithms in practice.
In this paper we introduce a covariance framework for the analysis of EEG and MEG data that takes into account observed temporal stationarity on small time scales and trial-to-trial variations. We formulate a model for the covariance matrix, which is a Kronecker product of three components that correspond to space, time and epochs/trials, and consider maximum likelihood estimation of the unknown parameter values. An iterative algorithm that finds approximations of the maximum likelihood estimates is proposed. We perform a simulation study to assess the performance of the estimator and investigate the influence of different assumptions about the covariance factors on the estimated covariance matrix and on its components. Apart from that, we illustrate our method on real EEG and MEG data sets. The proposed covariance model is applicable in a variety of cases where spontaneous EEG or MEG acts as source of noise and realistic noise covariance estimates are needed for accurate dipole localization, such as in evoked activity studies, or where the properties of spontaneous EEG or MEG are themselves the topic of interest, such as in combined EEG/fMRI experiments in which the correlation between EEG and fMRI signals is investigated.