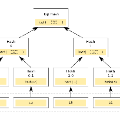
Motivated by a practical scenario in blockchains in which a client, who possesses a transaction, wishes to privately verify that the transaction actually belongs to a block, we investigate the problem of private retrieval of Merkle proofs (i.e. proofs of inclusion/membership) in a Merkle tree. In this setting, one or more servers store the nodes of a binary tree (a Merkle tree), while a client wants to retrieve the set of nodes along a root-to-leaf path (i.e. a Merkle proof, after appropriate node swapping operations), without letting the servers know which path is being retrieved. We propose a method that partitions the Merkle tree to enable parallel private retrieval of the Merkle proofs. The partitioning step is based on a novel tree coloring called ancestral coloring in which nodes that have ancestor-descendant relationship must have distinct colors. To minimize the retrieval time, the coloring is required to be balanced, i.e. the sizes of the color classes differ by at most one. We develop a fast algorithm to find a balanced (in fact, any) ancestral coloring in almost linear time in the number of tree nodes, which can handle trees with billions of nodes in a few minutes. Our partitioning method can be applied on top of any private information retrieval scheme, leading to the minimum storage overhead and fastest running times compared to existing approaches.
相關內容
The Geometric Brownian Motion (GBM) is a standard model in quantitative finance, but the potential function of its stochastic differential equation (SDE) cannot include stable nonzero prices. This article generalises the GBM to an SDE with polynomial drift of order q and shows via model selection that q=2 is most frequently the optimal model to describe the data. Moreover, Markov chain Monte Carlo ensembles of the accompanying potential functions show a clear and pronounced potential well, indicating the existence of a stable price.
Ordered sequences of data, specified with a join operation to combine sequences, serve as a foundation for the implementation of parallel functional algorithms. This abstract data type can be elegantly and efficiently implemented using balanced binary trees, where a join operation is provided to combine two trees and rebalance as necessary. In this work, we present a verified implementation and cost analysis of joinable red-black trees in $\textbf{calf}$, a dependent type theory for cost analysis. We implement red-black trees and auxiliary intermediate data structures in such a way that all correctness invariants are intrinsically maintained. Then, we describe and verify precise cost bounds on the operations, making use of the red-black tree invariants. Finally, we implement standard algorithms on sequences using the simple join-based signature and bound their cost in the case that red-black trees are used as the underlying implementation. All proofs are formally mechanized using the embedding of $\textbf{calf}$ in the Agda theorem prover.
PyPI provides a convenient and accessible package management platform to developers, enabling them to quickly implement specific functions and improve work efficiency. However, the rapid development of the PyPI ecosystem has led to a severe problem of malicious package propagation. Malicious developers disguise malicious packages as normal, posing a significant security risk to end-users. To this end, we conducted an empirical study to understand the characteristics and current state of the malicious code lifecycle in the PyPI ecosystem. We first built an automated data collection framework and collated a multi-source malicious code dataset containing 4,669 malicious package files. We preliminarily classified these malicious code into five categories based on malicious behaviour characteristics. Our research found that over 50% of malicious code exhibits multiple malicious behaviours, with information stealing and command execution being particularly prevalent. In addition, we observed several novel attack vectors and anti-detection techniques. Our analysis revealed that 74.81% of all malicious packages successfully entered end-user projects through source code installation, thereby increasing security risks. A real-world investigation showed that many reported malicious packages persist in PyPI mirror servers globally, with over 72% remaining for an extended period after being discovered. Finally, we sketched a portrait of the malicious code lifecycle in the PyPI ecosystem, effectively reflecting the characteristics of malicious code at different stages. We also present some suggested mitigations to improve the security of the Python open-source ecosystem.
Opioids are an effective analgesic for acute and chronic pain, but also carry a considerable risk of addiction leading to millions of opioid use disorder (OUD) cases and tens of thousands of premature deaths in the United States yearly. Estimating OUD risk prior to prescription could improve the efficacy of treatment regimens, monitoring programs, and intervention strategies, but risk estimation is typically based on self-reported data or questionnaires. We develop an experimental design and computational methods that combines genetic variants associated with OUD with behavioral features extracted from GPS and Wi-Fi spatiotemporal coordinates to assess OUD risk. Since both OUD mobility and genetic data do not exist for the same cohort, we develop algorithms to (1) generate mobility features from empirical distributions and (2) synthesize mobility and genetic samples assuming a level of comorbidity and relative risks. We show that integrating genetic and mobility modalities improves risk modelling using classification accuracy, area under the precision-recall and receiver operator characteristic curves, and $F_1$ score. Interpreting the fitted models suggests that mobility features have more influence on OUD risk, although the genetic contribution was significant, particularly in linear models. While there exists concerns with respect to privacy, security, bias, and generalizability that must be evaluated in clinical trials before being implemented in practice, our framework provides preliminary evidence that behavioral and genetic features may improve OUD risk estimation to assist with personalized clinical decision-making.
Analog computing has reemerged as a promising avenue for accelerating deep neural networks (DNNs) due to its potential to overcome the energy efficiency and scalability challenges posed by traditional digital architectures. However, achieving high precision and DNN accuracy using such technologies is challenging, as high-precision data converters are costly and impractical. In this paper, we address this challenge by using the residue number system (RNS). RNS allows composing high-precision operations from multiple low-precision operations, thereby eliminating the information loss caused by the limited precision of the data converters. Our study demonstrates that analog accelerators utilizing the RNS-based approach can achieve ${\geq}99\%$ of FP32 accuracy for state-of-the-art DNN inference using data converters with only $6$-bit precision whereas a conventional analog core requires more than $8$-bit precision to achieve the same accuracy in the same DNNs. The reduced precision requirements imply that using RNS can reduce the energy consumption of analog accelerators by several orders of magnitude while maintaining the same throughput and precision. Our study extends this approach to DNN training, where we can efficiently train DNNs using $7$-bit integer arithmetic while achieving accuracy comparable to FP32 precision. Lastly, we present a fault-tolerant dataflow using redundant RNS error-correcting codes to protect the computation against noise and errors inherent within an analog accelerator.
Performing inference in statistical models with an intractable likelihood is challenging, therefore, most likelihood-free inference (LFI) methods encounter accuracy and efficiency limitations. In this paper, we present the implementation of the LFI method Robust Optimisation Monte Carlo (ROMC) in the Python package ELFI. ROMC is a novel and efficient (highly-parallelizable) LFI framework that provides accurate weighted samples from the posterior. Our implementation can be used in two ways. First, a scientist may use it as an out-of-the-box LFI algorithm; we provide an easy-to-use API harmonized with the principles of ELFI, enabling effortless comparisons with the rest of the methods included in the package. Additionally, we have carefully split ROMC into isolated components for supporting extensibility. A researcher may experiment with novel method(s) for solving part(s) of ROMC without reimplementing everything from scratch. In both scenarios, the ROMC parts can run in a fully-parallelized manner, exploiting all CPU cores. We also provide helpful functionalities for (i) inspecting the inference process and (ii) evaluating the obtained samples. Finally, we test the robustness of our implementation on some typical LFI examples.
Large Language Models (LLMs) have shown excellent generalization capabilities that have led to the development of numerous models. These models propose various new architectures, tweaking existing architectures with refined training strategies, increasing context length, using high-quality training data, and increasing training time to outperform baselines. Analyzing new developments is crucial for identifying changes that enhance training stability and improve generalization in LLMs. This survey paper comprehensively analyses the LLMs architectures and their categorization, training strategies, training datasets, and performance evaluations and discusses future research directions. Moreover, the paper also discusses the basic building blocks and concepts behind LLMs, followed by a complete overview of LLMs, including their important features and functions. Finally, the paper summarizes significant findings from LLM research and consolidates essential architectural and training strategies for developing advanced LLMs. Given the continuous advancements in LLMs, we intend to regularly update this paper by incorporating new sections and featuring the latest LLM models.
We consider the problem of explaining the predictions of graph neural networks (GNNs), which otherwise are considered as black boxes. Existing methods invariably focus on explaining the importance of graph nodes or edges but ignore the substructures of graphs, which are more intuitive and human-intelligible. In this work, we propose a novel method, known as SubgraphX, to explain GNNs by identifying important subgraphs. Given a trained GNN model and an input graph, our SubgraphX explains its predictions by efficiently exploring different subgraphs with Monte Carlo tree search. To make the tree search more effective, we propose to use Shapley values as a measure of subgraph importance, which can also capture the interactions among different subgraphs. To expedite computations, we propose efficient approximation schemes to compute Shapley values for graph data. Our work represents the first attempt to explain GNNs via identifying subgraphs explicitly and directly. Experimental results show that our SubgraphX achieves significantly improved explanations, while keeping computations at a reasonable level.
Residual networks (ResNets) have displayed impressive results in pattern recognition and, recently, have garnered considerable theoretical interest due to a perceived link with neural ordinary differential equations (neural ODEs). This link relies on the convergence of network weights to a smooth function as the number of layers increases. We investigate the properties of weights trained by stochastic gradient descent and their scaling with network depth through detailed numerical experiments. We observe the existence of scaling regimes markedly different from those assumed in neural ODE literature. Depending on certain features of the network architecture, such as the smoothness of the activation function, one may obtain an alternative ODE limit, a stochastic differential equation or neither of these. These findings cast doubts on the validity of the neural ODE model as an adequate asymptotic description of deep ResNets and point to an alternative class of differential equations as a better description of the deep network limit.
We describe the new field of mathematical analysis of deep learning. This field emerged around a list of research questions that were not answered within the classical framework of learning theory. These questions concern: the outstanding generalization power of overparametrized neural networks, the role of depth in deep architectures, the apparent absence of the curse of dimensionality, the surprisingly successful optimization performance despite the non-convexity of the problem, understanding what features are learned, why deep architectures perform exceptionally well in physical problems, and which fine aspects of an architecture affect the behavior of a learning task in which way. We present an overview of modern approaches that yield partial answers to these questions. For selected approaches, we describe the main ideas in more detail.