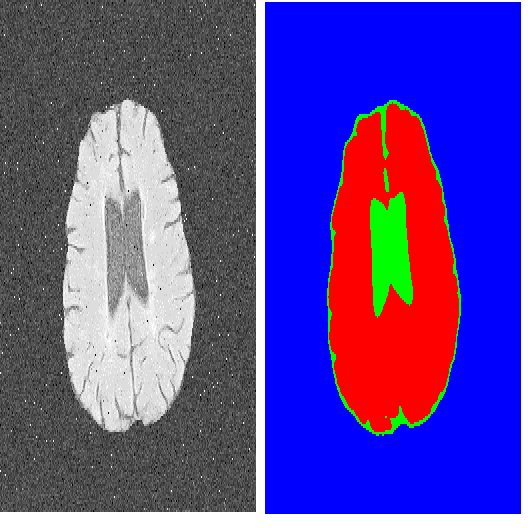
Given an image $u_0$, the aim of minimising the Mumford-Shah functional is to find a decomposition of the image domain into sub-domains and a piecewise smooth approximation $u$ of $u_0$ such that $u$ varies smoothly within each sub-domain. Since the Mumford-Shah functional is highly non-smooth, regularizations such as the Ambrosio-Tortorelli approximation can be considered which is one of the most computationally efficient approximations of the Mumford-Shah functional for image segmentation. While very impressive numerical results have been achieved in a large range of applications when minimising the functional, no analytical results are currently available for minimizers of the functional in the piecewise smooth setting, and this is the goal of this work. Our main result is the $\Gamma$-convergence of the Ambrosio-Tortorelli approximation of the Mumford-Shah functional for piecewise smooth approximations. This requires the introduction of an appropriate function space. As a consequence of our $\Gamma$-convergence result, we can infer the convergence of minimizers of the respective functionals.
相關內容
We study transfer learning in the context of estimating piecewise-constant signals when source data, which may be relevant but disparate, are available in addition to the target data. We initially investigate transfer learning estimators that respectively employ $\ell_1$- and $\ell_0$-penalties for unisource data scenarios and then generalise these estimators to accommodate multisource data. To further reduce estimation errors, especially in scenarios where some sources significantly differ from the target, we introduce an informative source selection algorithm. We then examine these estimators with multisource selection and establish their minimax optimality under specific regularity conditions. It is worth emphasising that, unlike the prevalent narrative in the transfer learning literature that the performance is enhanced through large source sample sizes, our approaches leverage higher observation frequencies and accommodate diverse frequencies across multiple sources. Our theoretical findings are empirically validated through extensive numerical experiments, with the code available online, see //github.com/chrisfanwang/transferlearning
Models of complex technological systems inherently contain interactions and dependencies among their input variables that affect their joint influence on the output. Such models are often computationally expensive and few sensitivity analysis methods can effectively process such complexities. Moreover, the sensitivity analysis field as a whole pays limited attention to the nature of interaction effects, whose understanding can prove to be critical for the design of safe and reliable systems. In this paper, we introduce and extensively test a simple binning approach for computing sensitivity indices and demonstrate how complementing it with the smart visualization method, simulation decomposition (SimDec), can permit important insights into the behavior of complex engineering models. The simple binning approach computes first-, second-order effects, and a combined sensitivity index, and is considerably more computationally efficient than Sobol' indices. The totality of the sensitivity analysis framework provides an efficient and intuitive way to analyze the behavior of complex systems containing interactions and dependencies.
We describe a new dependent-rounding algorithmic framework for bipartite graphs. Given a fractional assignment $y$ of values to edges of graph $G = (U \cup V, E)$, the algorithms return an integral solution $Y$ such that each right-node $v \in V$ has at most one neighboring edge $f$ with $Y_f = 1$, and where the variables $Y_e$ also satisfy broad nonpositive-correlation properties. In particular, for any edges $e_1, e_2$ sharing a left-node $u \in U$, the variables $Y_{e_1}, Y_{e_2}$ have strong negative-correlation properties, i.e. the expectation of $Y_{e_1} Y_{e_2}$ is significantly below $y_{e_1} y_{e_2}$. This algorithm is based on generating negatively-correlated Exponential random variables and using them in a contention-resolution scheme inspired by an algorithm Im & Shadloo (2020). Our algorithm gives stronger and much more flexible negative correlation properties. Dependent rounding schemes with negative correlation properties have been used for approximation algorithms for job-scheduling on unrelated machines to minimize weighted completion times (Bansal, Srinivasan, & Svensson (2021), Im & Shadloo (2020), Im & Li (2023)). Using our new dependent-rounding algorithm, among other improvements, we obtain a $1.4$-approximation for this problem. This significantly improves over the prior $1.45$-approximation ratio of Im & Li (2023).
We present a semi-Lagrangian characteristic mapping method for the incompressible Euler equations on a rotating sphere. The numerical method uses a spatio-temporal discretization of the inverse flow map generated by the Eulerian velocity as a composition of sub-interval flows formed by $C^1$ spherical spline interpolants. This approximation technique has the capacity of resolving sub-grid scales generated over time without increasing the spatial resolution of the computational grid. The numerical method is analyzed and validated using standard test cases yielding third-order accuracy in the supremum norm. Numerical experiments illustrating the unique resolution properties of the method are performed and demonstrate the ability to reproduce the forward energy cascade at sub-grid scales by upsampling the numerical solution.
Rational function approximations provide a simple but flexible alternative to polynomial approximation, allowing one to capture complex non-linearities without oscillatory artifacts. However, there have been few attempts to use rational functions on noisy data due to the likelihood of creating spurious singularities. To avoid the creation of singularities, we use Bernstein polynomials and appropriate conditions on their coefficients to force the denominator to be strictly positive. While this reduces the range of rational polynomials that can be expressed, it keeps all the benefits of rational functions while maintaining the robustness of polynomial approximation in noisy data scenarios. Our numerical experiments on noisy data show that existing rational approximation methods continually produce spurious poles inside the approximation domain. This contrasts our method, which cannot create poles in the approximation domain and provides better fits than a polynomial approximation and even penalized splines on functions with multiple variables. Moreover, guaranteeing pole-free in an interval is critical for estimating non-constant coefficients when numerically solving differential equations using spectral methods. This provides a compact representation of the original differential equation, allowing numeric solvers to achieve high accuracy quickly, as seen in our experiments.
Determining the weight distribution of a code is an old and fundamental topic in coding theory that has been thoroughly studied. In 1977, Helleseth, Kl{\o}ve, and Mykkeltveit presented a weight enumerator polynomial of the lifted code over $\mathbb{F}_{q^\ell}$ of a $q$-ary linear code with significant combinatorial properties, which can determine the support weight distribution of this linear code. The Solomon-Stiffler codes are a family of famous Griesmer codes, which were proposed by Solomon and Stiffler in 1965. In this paper, we determine the weight enumerator polynomials of the lifted codes of the projective Solomon-Stiffler codes using some combinatorial properties of subspaces. As a result, we determine the support weight distributions of the projective Solomon-Stiffler codes. In particular, we determine the weight hierarchies of the projective Solomon-Stiffler codes.
In this article, we focus on the error that is committed when computing the matrix logarithm using the Gauss--Legendre quadrature rules. These formulas can be interpreted as Pad\'e approximants of a suitable Gauss hypergeometric function. Empirical observation tells us that the convergence of these quadratures becomes slow when the matrix is not close to the identity matrix, thus suggesting the usage of an inverse scaling and squaring approach for obtaining a matrix with this property. The novelty of this work is the introduction of error estimates that can be used to select a priori both the number of Legendre points needed to obtain a given accuracy and the number of inverse scaling and squaring to be performed. We include some numerical experiments to show the reliability of the estimates introduced.
We investigate the randomized decision tree complexity of a specific class of read-once threshold functions. A read-once threshold formula can be defined by a rooted tree, every internal node of which is labeled by a threshold function $T_k^n$ (with output 1 only when at least $k$ out of $n$ input bits are 1) and each leaf by a distinct variable. Such a tree defines a Boolean function in a natural way. We focus on the randomized decision tree complexity of such functions, when the underlying tree is a uniform tree with all its internal nodes labeled by the same threshold function. We prove lower bounds of the form $c(k,n)^d$, where $d$ is the depth of the tree. We also treat trees with alternating levels of AND and OR gates separately and show asymptotically optimal bounds, extending the known bounds for the binary case.
A modelling framework suitable for detecting shape shifts in functional profiles combining the notion of Fr\'echet mean and the concept of deformation models is developed and proposed. The generalized mean sense offered by the Fr\'echet mean notion is employed to capture the typical pattern of the profiles under study, while the concept of deformation models, and in particular of the shape invariant model, allows for interpretable parameterizations of profile's deviations from the typical shape. EWMA-type control charts compatible with the functional nature of data and the employed deformation model are built and proposed, exploiting certain shape characteristics of the profiles under study with respect to the generalized mean sense, allowing for the identification of potential shifts concerning the shape and/or the deformation process. Potential shifts in the shape deformation process, are further distinguished to significant shifts with respect to amplitude and/or the phase of the profile under study. The proposed modelling and shift detection framework is implemented to a real world case study, where daily concentration profiles concerning air pollutants from an area in the city of Athens are modelled, while profiles indicating hazardous concentration levels are successfully identified in most of the cases.
HyperNetX (HNX) is an open source Python library for the analysis and visualization of complex network data modeled as hypergraphs. Initially released in 2019, HNX facilitates exploratory data analysis of complex networks using algebraic topology, combinatorics, and generalized hypergraph and graph theoretical methods on structured data inputs. With its 2023 release, the library supports attaching metadata, numerical and categorical, to nodes (vertices) and hyperedges, as well as to node-hyperedge pairings (incidences). HNX has a customizable Matplotlib-based visualization module as well as HypernetX-Widget, its JavaScript addon for interactive exploration and visualization of hypergraphs within Jupyter Notebooks. Both packages are available on GitHub and PyPI. With a growing community of users and collaborators, HNX has become a preeminent tool for hypergraph analysis.