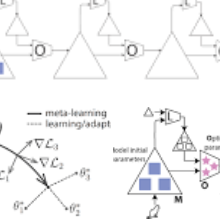
Conventional optimization methods in machine learning and controls rely heavily on first-order update rules. Selecting the right method and hyperparameters for a particular task often involves trial-and-error or practitioner intuition, motivating the field of meta-learning. We generalize a broad family of preexisting update rules by proposing a meta-learning framework in which the inner loop optimization step involves solving a differentiable convex optimization (DCO). We illustrate the theoretical appeal of this approach by showing that it enables one-step optimization of a family of linear least squares problems, given that the meta-learner has sufficient exposure to similar tasks. Various instantiations of the DCO update rule are compared to conventional optimizers on a range of illustrative experimental settings.
相關內容
Foundation Models (FMs), such as BERT, GPT, ViT, and CLIP, have demonstrated remarkable success in a wide range of applications, driven by their ability to leverage vast amounts of data for pre-training. However, optimizing FMs often requires access to sensitive data, raising privacy concerns and limiting their applicability in certain domains. In this paper, we introduce the concept of Federated Foundation Models (FFMs), a novel approach that combines the benefits of FMs and Federated Learning (FL) to enable privacy-preserving and collaborative learning across multiple institutions. We discuss the potential benefits and challenges of integrating FL into the lifespan of FMs, covering pre-training, fine-tuning, and application. We further provide formal definitions of FFM tasks, including FFM pre-training, FFM fine-tuning, and federated prompt engineering, allowing for more personalized and context-aware models while maintaining data privacy. Moreover, we explore the possibility of continual/lifelong learning in FFMs, as increased computational power at the edge unlocks the potential for optimizing FMs using newly generated private data at edges. We present experiments and evaluations comparing the performance of FFMs to traditional FMs on various downstream tasks, demonstrating the effectiveness of our approach in preserving privacy, reducing overfitting, and improving model generalizability. The proposed Federated Foundation Models offer a flexible and scalable framework for training large language models in a privacy-preserving manner, paving the way for future advancements in both FM pre-training and federated learning.
This article proposes a meta-learning method for estimating the conditional average treatment effect (CATE) from a few observational data. The proposed method learns how to estimate CATEs from multiple tasks and uses the knowledge for unseen tasks. In the proposed method, based on the meta-learner framework, we decompose the CATE estimation problem into sub-problems. For each sub-problem, we formulate our estimation models using neural networks with task-shared and task-specific parameters. With our formulation, we can obtain optimal task-specific parameters in a closed form that are differentiable with respect to task-shared parameters, making it possible to perform effective meta-learning. The task-shared parameters are trained such that the expected CATE estimation performance in few-shot settings is improved by minimizing the difference between a CATE estimated with a large amount of data and one estimated with just a few data. Our experimental results demonstrate that our method outperforms the existing meta-learning approaches and CATE estimation methods.
Research in machine learning has polarized into two general approaches for regression tasks: Transductive methods construct estimates directly from available data but are usually problem unspecific. Inductive methods can be much more specific but generally require compute-intensive solution searches. In this work, we propose a hybrid approach and show that transductive regression principles can be meta-learned through gradient descent to form efficient in-context neural approximators by leveraging the theory of vector-valued Reproducing Kernel Banach Spaces (RKBS). We apply this approach to function spaces defined over finite and infinite-dimensional spaces (function-valued operators) and show that once trained, the Transducer can almost instantaneously capture an infinity of functional relationships given a few pairs of input and output examples and return new image estimates. We demonstrate the benefit of our meta-learned transductive approach to model complex physical systems influenced by varying external factors with little data at a fraction of the usual deep learning training computational cost for partial differential equations and climate modeling applications.
Robots often rely on a repertoire of previously-learned motion policies for performing tasks of diverse complexities. When facing unseen task conditions or when new task requirements arise, robots must adapt their motion policies accordingly. In this context, policy optimization is the \emph{de facto} paradigm to adapt robot policies as a function of task-specific objectives. Most commonly-used motion policies carry particular structures that are often overlooked in policy optimization algorithms. We instead propose to leverage the structure of probabilistic policies by casting the policy optimization as an optimal transport problem. Specifically, we focus on robot motion policies that build on Gaussian mixture models (GMMs) and formulate the policy optimization as a Wassertein gradient flow over the GMMs space. This naturally allows us to constrain the policy updates via the $L^2$-Wasserstein distance between GMMs to enhance the stability of the policy optimization process. Furthermore, we leverage the geometry of the Bures-Wasserstein manifold to optimize the Gaussian distributions of the GMM policy via Riemannian optimization. We evaluate our approach on common robotic settings: Reaching motions, collision-avoidance behaviors, and multi-goal tasks. Our results show that our method outperforms common policy optimization baselines in terms of task success rate and low-variance solutions.
Reinforcement Learning (RL) with constraints is becoming an increasingly important problem for various applications. Often, the average criterion is more suitable than the discounted criterion. Yet, RL for average criterion-constrained MDPs remains a challenging problem. Algorithms designed for discounted constrained RL problems often do not perform well for the average CMDP setting. In this paper, we introduce a new policy optimization with function approximation algorithm for constrained MDPs with the average criterion. The Average-Constrained Policy Optimization (ACPO) algorithm is inspired by the famed PPO-type algorithms based on trust region methods. We develop basic sensitivity theory for average MDPs, and then use the corresponding bounds in the design of the algorithm. We provide theoretical guarantees on its performance, and through extensive experimental work in various challenging MuJoCo environments, show the superior performance of the algorithm when compared to other state-of-the-art algorithms adapted for the average CMDP setting.
This work, for the first time, introduces two constant factor approximation algorithms with linear query complexity for non-monotone submodular maximization over a ground set of size $n$ subject to a knapsack constraint, $\mathsf{DLA}$ and $\mathsf{RLA}$. $\mathsf{DLA}$ is a deterministic algorithm that provides an approximation factor of $6+\epsilon$ while $\mathsf{RLA}$ is a randomized algorithm with an approximation factor of $4+\epsilon$. Both run in $O(n \log(1/\epsilon)/\epsilon)$ query complexity. The key idea to obtain a constant approximation ratio with linear query lies in: (1) dividing the ground set into two appropriate subsets to find the near-optimal solution over these subsets with linear queries, and (2) combining a threshold greedy with properties of two disjoint sets or a random selection process to improve solution quality. In addition to the theoretical analysis, we have evaluated our proposed solutions with three applications: Revenue Maximization, Image Summarization, and Maximum Weighted Cut, showing that our algorithms not only return comparative results to state-of-the-art algorithms but also require significantly fewer queries.
The conjoining of dynamical systems and deep learning has become a topic of great interest. In particular, neural differential equations (NDEs) demonstrate that neural networks and differential equation are two sides of the same coin. Traditional parameterised differential equations are a special case. Many popular neural network architectures, such as residual networks and recurrent networks, are discretisations. NDEs are suitable for tackling generative problems, dynamical systems, and time series (particularly in physics, finance, ...) and are thus of interest to both modern machine learning and traditional mathematical modelling. NDEs offer high-capacity function approximation, strong priors on model space, the ability to handle irregular data, memory efficiency, and a wealth of available theory on both sides. This doctoral thesis provides an in-depth survey of the field. Topics include: neural ordinary differential equations (e.g. for hybrid neural/mechanistic modelling of physical systems); neural controlled differential equations (e.g. for learning functions of irregular time series); and neural stochastic differential equations (e.g. to produce generative models capable of representing complex stochastic dynamics, or sampling from complex high-dimensional distributions). Further topics include: numerical methods for NDEs (e.g. reversible differential equations solvers, backpropagation through differential equations, Brownian reconstruction); symbolic regression for dynamical systems (e.g. via regularised evolution); and deep implicit models (e.g. deep equilibrium models, differentiable optimisation). We anticipate this thesis will be of interest to anyone interested in the marriage of deep learning with dynamical systems, and hope it will provide a useful reference for the current state of the art.
It has been shown that deep neural networks are prone to overfitting on biased training data. Towards addressing this issue, meta-learning employs a meta model for correcting the training bias. Despite the promising performances, super slow training is currently the bottleneck in the meta learning approaches. In this paper, we introduce a novel Faster Meta Update Strategy (FaMUS) to replace the most expensive step in the meta gradient computation with a faster layer-wise approximation. We empirically find that FaMUS yields not only a reasonably accurate but also a low-variance approximation of the meta gradient. We conduct extensive experiments to verify the proposed method on two tasks. We show our method is able to save two-thirds of the training time while still maintaining the comparable or achieving even better generalization performance. In particular, our method achieves the state-of-the-art performance on both synthetic and realistic noisy labels, and obtains promising performance on long-tailed recognition on standard benchmarks.
Federated learning enables multiple parties to collaboratively train a machine learning model without communicating their local data. A key challenge in federated learning is to handle the heterogeneity of local data distribution across parties. Although many studies have been proposed to address this challenge, we find that they fail to achieve high performance in image datasets with deep learning models. In this paper, we propose MOON: model-contrastive federated learning. MOON is a simple and effective federated learning framework. The key idea of MOON is to utilize the similarity between model representations to correct the local training of individual parties, i.e., conducting contrastive learning in model-level. Our extensive experiments show that MOON significantly outperforms the other state-of-the-art federated learning algorithms on various image classification tasks.
Recently, graph neural networks (GNNs) have revolutionized the field of graph representation learning through effectively learned node embeddings, and achieved state-of-the-art results in tasks such as node classification and link prediction. However, current GNN methods are inherently flat and do not learn hierarchical representations of graphs---a limitation that is especially problematic for the task of graph classification, where the goal is to predict the label associated with an entire graph. Here we propose DiffPool, a differentiable graph pooling module that can generate hierarchical representations of graphs and can be combined with various graph neural network architectures in an end-to-end fashion. DiffPool learns a differentiable soft cluster assignment for nodes at each layer of a deep GNN, mapping nodes to a set of clusters, which then form the coarsened input for the next GNN layer. Our experimental results show that combining existing GNN methods with DiffPool yields an average improvement of 5-10% accuracy on graph classification benchmarks, compared to all existing pooling approaches, achieving a new state-of-the-art on four out of five benchmark data sets.