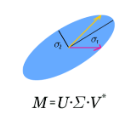
A flexible transform-based tensor product named $\star_{{\rm{QT}}}$-product for $L$th-order ($L\geq 3$) quaternion tensors is proposed. Based on the $\star_{{\rm{QT}}}$-product, we define the corresponding singular value decomposition named TQt-SVD and the rank named TQt-rank of the $L$th-order ($L\geq 3$) quaternion tensor. Furthermore, with orthogonal quaternion transformations, the TQt-SVD can provide the best TQt-rank-$s$ approximation of any $L$th-order ($L\geq 3$) quaternion tensor. In the experiments, we have verified the effectiveness of the proposed TQt-SVD in the application of the best TQt-rank-$s$ approximation for color videos represented by third-order quaternion tensors.
相關內容
We study the problem of selling information to a data-buyer who faces a decision problem under uncertainty. We consider the classic Bayesian decision-theoretic model pioneered by [Blackwell, 1951, 1953]. Initially, the data buyer has only partial information about the payoff-relevant state of the world. A data seller offers additional information about the state of the world. The information is revealed through signaling schemes, also referred to as experiments. In the single-agent setting, any mechanism can be represented as a menu of experiments. [Bergemann et al., 2018] present a complete characterization of the revenue-optimal mechanism in a binary state and binary action environment. By contrast, no characterization is known for the case with more actions. In this paper, we consider more general environments and study arguably the simplest mechanism, which only sells the fully informative experiment. In the environment with binary state and $m\geq 3$ actions, we provide an $O(m)$-approximation to the optimal revenue by selling only the fully informative experiment and show that the approximation ratio is tight up to an absolute constant factor. An important corollary of our lower bound is that the size of the optimal menu must grow at least linearly in the number of available actions, so no universal upper bound exists for the size of the optimal menu in the general single-dimensional setting. For multi-dimensional environments, we prove that even in arguably the simplest matching utility environment with 3 states and 3 actions, the ratio between the optimal revenue and the revenue by selling only the fully informative experiment can grow immediately to a polynomial of the number of agent types. Nonetheless, if the distribution is uniform, we show that selling only the fully informative experiment is indeed the optimal mechanism.
We present a classical algorithm that, for any $D$-dimensional geometrically-local, quantum circuit $C$ of polylogarithmic-depth, and any bit string $x \in {0,1}^n$, can compute the quantity $|<x|C|0^{\otimes n}>|^2$ to within any inverse-polynomial additive error in quasi-polynomial time, for any fixed dimension $D$. This is an extension of the result [CC21], which originally proved this result for $D = 3$. To see why this is interesting, note that, while the $D = 1$ case of this result follows from standard use of Matrix Product States, known for decades, the $D = 2$ case required novel and interesting techniques introduced in [BGM19]. Extending to the case $D = 3$ was even more laborious and required further new techniques introduced in [CC21]. Our work here shows that, while handling each new dimension has historically required a new insight, and fixed algorithmic primitive, based on known techniques for $D \leq 3$, we can now handle any fixed dimension $D > 3$. Our algorithm uses the Divide-and-Conquer framework of [CC21] to approximate the desired quantity via several instantiations of the same problem type, each involving $D$-dimensional circuits on about half the number of qubits as the original. This division step is then applied recursively, until the width of the recursively decomposed circuits in the $D^{th}$ dimension is so small that they can effectively be regarded as $(D-1)$-dimensional problems by absorbing the small width in the $D^{th}$ dimension into the qudit structure at the cost of a moderate increase in runtime. The main technical challenge lies in ensuring that the more involved portions of the recursive circuit decomposition and error analysis from [CC21] still hold in higher dimensions, which requires small modifications to the analysis in some places.
We advocate for the use of dual quaternions to represent poses and twists for robotics. We show how to represent torques and forces using dual quaternions. We introduce the notion of the Lie derivative, and explain how it can be used to calculate the behavior of actuators. We show how to combine dual quaternions with the Newton-Raphson method to compute forward kinematics for parallel robots. We derive the equations of motion in dual quaternion form. This paper contains results we have not seen before, which are listed in the conclusion.
This paper is concerned with two improved variants of the Hutch++ algorithm for estimating the trace of a square matrix, implicitly given through matrix-vector products. Hutch++ combines randomized low-rank approximation in a first phase with stochastic trace estimation in a second phase. In turn, Hutch++ only requires $O\left(\varepsilon^{-1}\right)$ matrix-vector products to approximate the trace within a relative error $\varepsilon$ with high probability. This compares favorably with the $O\left(\varepsilon^{-2}\right)$ matrix-vector products needed when using stochastic trace estimation alone. In Hutch++, the number of matrix-vector products is fixed a priori and distributed in a prescribed fashion among the two phases. In this work, we derive an adaptive variant of Hutch++, which outputs an estimate of the trace that is within some prescribed error tolerance with a controllable failure probability, while splitting the matrix-vector products in a near-optimal way among the two phases. For the special case of symmetric positive semi-definite matrix, we present another variant of Hutch++, called Nystr\"om++, which utilizes the so called Nystr\"om approximation and requires only one pass over the matrix, as compared to two passes with Hutch++. We extend the analysis of Hutch++ to Nystr\"om++. Numerical experiments demonstrate the effectiveness of our two new algorithms.
We develop methodology for testing hypotheses regarding the slope function in functional linear regression for time series via a reproducing kernel Hilbert space approach. In contrast to most of the literature, which considers tests for the exact nullity of the slope function, we are interested in the null hypothesis that the slope function vanishes only approximately, where deviations are measured with respect to the $L^2$-norm. An asymptotically pivotal test is proposed, which does not require the estimation of nuisance parameters and long-run covariances. The key technical tools to prove the validity of our approach include a uniform Bahadur representation and a weak invariance principle for a sequential process of estimates of the slope function. Both scalar-on-function and function-on-function linear regression are considered and finite-sample methods for implementing our methodology are provided. We also illustrate the potential of our methods by means of a small simulation study and a data example.
Computing the top eigenvectors of a matrix is a problem of fundamental interest to various fields. While the majority of the literature has focused on analyzing the reconstruction error of low-rank matrices associated with the retrieved eigenvectors, in many applications one is interested in finding one vector with high Rayleigh quotient. In this paper we study the problem of approximating the top-eigenvector. Given a symmetric matrix $\mathbf{A}$ with largest eigenvalue $\lambda_1$, our goal is to find a vector \hu that approximates the leading eigenvector $\mathbf{u}_1$ with high accuracy, as measured by the ratio $R(\hat{\mathbf{u}})=\lambda_1^{-1}{\hat{\mathbf{u}}^T\mathbf{A}\hat{\mathbf{u}}}/{\hat{\mathbf{u}}^T\hat{\mathbf{u}}}$. We present a novel analysis of the randomized SVD algorithm of \citet{halko2011finding} and derive tight bounds in many cases of interest. Notably, this is the first work that provides non-trivial bounds of $R(\hat{\mathbf{u}})$ for randomized SVD with any number of iterations. Our theoretical analysis is complemented with a thorough experimental study that confirms the efficiency and accuracy of the method.
We present a constant-round algorithm in the massively parallel computation (MPC) model for evaluating a natural join where every input relation has two attributes. Our algorithm achieves a load of $\tilde{O}(m/p^{1/\rho})$ where $m$ is the total size of the input relations, $p$ is the number of machines, $\rho$ is the join's fractional edge covering number, and $\tilde{O}(.)$ hides a polylogarithmic factor. The load matches a known lower bound up to a polylogarithmic factor. At the core of the proposed algorithm is a new theorem (which we name {\em the isolated cartesian product theorem}) that provides fresh insight into the problem's mathematical structure. Our result implies that the {\em subgraph enumeration problem}, where the goal is to report all the occurrences of a constant-sized subgraph pattern, can be settled optimally (up to a polylogarithmic factor) in the MPC model.
Singularity subtraction for linear weakly singular Fredholm integral equations of the second kind is generalized to nonlinear integral equations. Two approaches are presented: The Classical Approach discretizes the nonlinear problem, and uses some finite dimensional linearization process to solve numerically the discrete problem. Its convergence is proved under mild hypotheses on the nonlinearity and the quadrature rule of the singularity subtraction scheme. The New Approach is based on linearization of the problem in its infinite dimensional setting, and discretization of the sequence of linear problems by singularity subtraction. It is more efficient than the former, as two numerical experiments confirm.
In recent years, knowledge graph completion methods have been extensively studied, in which graph embedding approaches learn low dimensional representations of entities and relations to predict missing facts. Those models usually view the relation vector as a translation (TransE) or rotation (rotatE and QuatE) between entity pairs, enjoying the advantage of simplicity and efficiency. However, QuatE has two main problems: 1) The model to capture the ability of representation and feature interaction between entities and relations are relatively weak because it only relies on the rigorous calculation of three embedding vectors; 2) Although the model can handle various relation patterns including symmetry, anti-symmetry, inversion and composition, but mapping properties of relations are not to be considered, such as one-to-many, many-to-one, and many-to-many. In this paper, we propose a novel model, QuatDE, with a dynamic mapping strategy to explicitly capture a variety of relational patterns, enhancing the feature interaction capability between elements of the triplet. Our model relies on three extra vectors donated as subject transfer vector, object transfer vector and relation transfer vector. The mapping strategy dynamically selects the transition vectors associated with each triplet, used to adjust the point position of the entity embedding vectors in the quaternion space via Hamilton product. Experiment results show QuatDE achieves state-of-the-art performance on three well-established knowledge graph completion benchmarks. In particular, the MR evaluation has relatively increased by 26% on WN18 and 15% on WN18RR, which proves the generalization of QuatDE.
The main contribution of this paper is a new submap joining based approach for solving large-scale Simultaneous Localization and Mapping (SLAM) problems. Each local submap is independently built using the local information through solving a small-scale SLAM; the joining of submaps mainly involves solving linear least squares and performing nonlinear coordinate transformations. Through approximating the local submap information as the state estimate and its corresponding information matrix, judiciously selecting the submap coordinate frames, and approximating the joining of a large number of submaps by joining only two maps at a time, either sequentially or in a more efficient Divide and Conquer manner, the nonlinear optimization process involved in most of the existing submap joining approaches is avoided. Thus the proposed submap joining algorithm does not require initial guess or iterations since linear least squares problems have closed-form solutions. The proposed Linear SLAM technique is applicable to feature-based SLAM, pose graph SLAM and D-SLAM, in both two and three dimensions, and does not require any assumption on the character of the covariance matrices. Simulations and experiments are performed to evaluate the proposed Linear SLAM algorithm. Results using publicly available datasets in 2D and 3D show that Linear SLAM produces results that are very close to the best solutions that can be obtained using full nonlinear optimization algorithm started from an accurate initial guess. The C/C++ and MATLAB source codes of Linear SLAM are available on OpenSLAM.