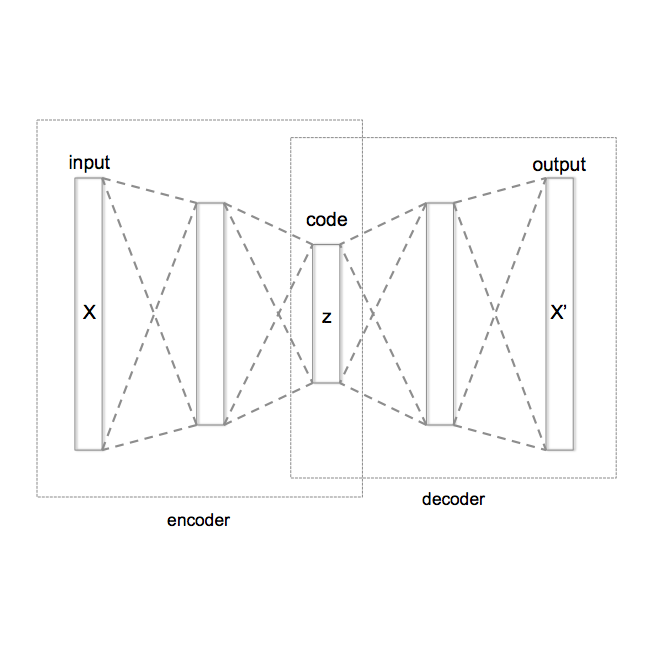
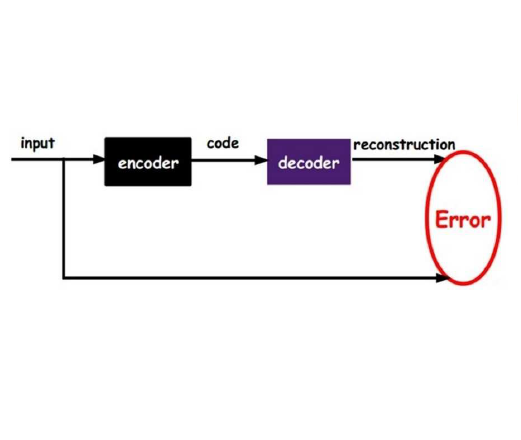
Despite its wide use and empirical successes, the theoretical understanding and study of the behaviour and performance of the variational autoencoder (VAE) have only emerged in the past few years. We contribute to this recent line of work by analysing the VAE's reconstruction ability for unseen test data, leveraging arguments from the PAC-Bayes theory. We provide generalisation bounds on the theoretical reconstruction error, and provide insights on the regularisation effect of VAE objectives. We illustrate our theoretical results with supporting experiments on classical benchmark datasets.
相關內容
Unsupervised domain adaptation approaches have recently succeeded in various medical image segmentation tasks. The reported works often tackle the domain shift problem by aligning the domain-invariant features and minimizing the domain-specific discrepancies. That strategy works well when the difference between a specific domain and between different domains is slight. However, the generalization ability of these models on diverse imaging modalities remains a significant challenge. This paper introduces UDA-VAE++, an unsupervised domain adaptation framework for cardiac segmentation with a compact loss function lower bound. To estimate this new lower bound, we develop a novel Structure Mutual Information Estimation (SMIE) block with a global estimator, a local estimator, and a prior information matching estimator to maximize the mutual information between the reconstruction and segmentation tasks. Specifically, we design a novel sequential reparameterization scheme that enables information flow and variance correction from the low-resolution latent space to the high-resolution latent space. Comprehensive experiments on benchmark cardiac segmentation datasets demonstrate that our model outperforms previous state-of-the-art qualitatively and quantitatively. The code is available at //github.com/LOUEY233/Toward-Mutual-Information}{//github.com/LOUEY233/Toward-Mutual-Information
We present a data-efficient framework for solving sequential decision-making problems which exploits the combination of reinforcement learning (RL) and latent variable generative models. The framework, called GenRL, trains deep policies by introducing an action latent variable such that the feed-forward policy search can be divided into two parts: (i) training a sub-policy that outputs a distribution over the action latent variable given a state of the system, and (ii) unsupervised training of a generative model that outputs a sequence of motor actions conditioned on the latent action variable. GenRL enables safe exploration and alleviates the data-inefficiency problem as it exploits prior knowledge about valid sequences of motor actions. Moreover, we provide a set of measures for evaluation of generative models such that we are able to predict the performance of the RL policy training prior to the actual training on a physical robot. We experimentally determine the characteristics of generative models that have most influence on the performance of the final policy training on two robotics tasks: shooting a hockey puck and throwing a basketball. Furthermore, we empirically demonstrate that GenRL is the only method which can safely and efficiently solve the robotics tasks compared to two state-of-the-art RL methods.
The presence of noise is an intrinsic problem in acquisition processes for digital images. One way to enhance images is to combine the forward and backward diffusion equations. However, the latter problem is well known to be exponentially unstable with respect to any small perturbations on the final data. In this scenario, the final data can be regarded as a blurred image obtained from the forward process, and that image can be pixelated as a network. Therefore, we study in this work a regularization framework for the backward diffusion equation on graphs. Our aim is to construct a spectral graph-based solution based upon a cut-off projection. Stability and convergence results are provided together with some numerical experiments.
Gaussian process regression is increasingly applied for learning unknown dynamical systems. In particular, the implicit quantification of the uncertainty of the learned model makes it a promising approach for safety-critical applications. When using Gaussian process regression to learn unknown systems, a commonly considered approach consists of learning the residual dynamics after applying some generic discretization technique, which might however disregard properties of the underlying physical system. Variational integrators are a less common yet promising approach to discretization, as they retain physical properties of the underlying system, such as energy conservation and satisfaction of explicit kinematic constraints. In this work, we present a novel structure-preserving learning-based modelling approach that combines a variational integrator for the nominal dynamics of a mechanical system and learning residual dynamics with Gaussian process regression. We extend our approach to systems with known kinematic constraints and provide formal bounds on the prediction uncertainty. The simulative evaluation of the proposed method shows desirable energy conservation properties in accordance with general theoretical results and demonstrates exact constraint satisfaction for constrained dynamical systems.
In this paper, we propose a PAC-Bayesian \textit{a posteriori} parameter selection scheme for adaptive regularized regression in Hilbert scales under general, unknown source conditions. We demonstrate that our approach is adaptive to misspecification, and achieves the optimal learning rate under subgaussian noise. Unlike existing parameter selection schemes, the computational complexity of our approach is independent of sample size. We derive minimax adaptive rates for a new, broad class of Tikhonov-regularized learning problems under general, misspecified source conditions, that notably do not require any conventional a priori assumptions on kernel eigendecay. Using the theory of interpolation, we demonstrate that the spectrum of the Mercer operator can be inferred in the presence of "tight" $L^{\infty}$ embeddings of suitable Hilbert scales. Finally, we prove, that under a $\Delta_2$ condition on the smoothness index functions, our PAC-Bayesian scheme can indeed achieve minimax rates. We discuss applications of our approach to statistical inverse problems and oracle-efficient contextual bandit algorithms.
This study clarifies the proper criteria to assess the modeling capacity of a general tensor model. The work analyze the problem based on the study of tensor ranks, which is not a well-defined quantity for higher order tensors. To process, the author introduces the separability issue to discuss the Cannikin's law of tensor modeling. Interestingly, a connection between entanglement studied in information theory and tensor analysis is established, shedding new light on the theoretical understanding for modeling capacity problems.
The adaptive processing of structured data is a long-standing research topic in machine learning that investigates how to automatically learn a mapping from a structured input to outputs of various nature. Recently, there has been an increasing interest in the adaptive processing of graphs, which led to the development of different neural network-based methodologies. In this thesis, we take a different route and develop a Bayesian Deep Learning framework for graph learning. The dissertation begins with a review of the principles over which most of the methods in the field are built, followed by a study on graph classification reproducibility issues. We then proceed to bridge the basic ideas of deep learning for graphs with the Bayesian world, by building our deep architectures in an incremental fashion. This framework allows us to consider graphs with discrete and continuous edge features, producing unsupervised embeddings rich enough to reach the state of the art on several classification tasks. Our approach is also amenable to a Bayesian nonparametric extension that automatizes the choice of almost all model's hyper-parameters. Two real-world applications demonstrate the efficacy of deep learning for graphs. The first concerns the prediction of information-theoretic quantities for molecular simulations with supervised neural models. After that, we exploit our Bayesian models to solve a malware-classification task while being robust to intra-procedural code obfuscation techniques. We conclude the dissertation with an attempt to blend the best of the neural and Bayesian worlds together. The resulting hybrid model is able to predict multimodal distributions conditioned on input graphs, with the consequent ability to model stochasticity and uncertainty better than most works. Overall, we aim to provide a Bayesian perspective into the articulated research field of deep learning for graphs.
In this paper, we propose a novel Feature Decomposition and Reconstruction Learning (FDRL) method for effective facial expression recognition. We view the expression information as the combination of the shared information (expression similarities) across different expressions and the unique information (expression-specific variations) for each expression. More specifically, FDRL mainly consists of two crucial networks: a Feature Decomposition Network (FDN) and a Feature Reconstruction Network (FRN). In particular, FDN first decomposes the basic features extracted from a backbone network into a set of facial action-aware latent features to model expression similarities. Then, FRN captures the intra-feature and inter-feature relationships for latent features to characterize expression-specific variations, and reconstructs the expression feature. To this end, two modules including an intra-feature relation modeling module and an inter-feature relation modeling module are developed in FRN. Experimental results on both the in-the-lab databases (including CK+, MMI, and Oulu-CASIA) and the in-the-wild databases (including RAF-DB and SFEW) show that the proposed FDRL method consistently achieves higher recognition accuracy than several state-of-the-art methods. This clearly highlights the benefit of feature decomposition and reconstruction for classifying expressions.
Graph Neural Networks (GNNs) are widely used for analyzing graph-structured data. Most GNN methods are highly sensitive to the quality of graph structures and usually require a perfect graph structure for learning informative embeddings. However, the pervasiveness of noise in graphs necessitates learning robust representations for real-world problems. To improve the robustness of GNN models, many studies have been proposed around the central concept of Graph Structure Learning (GSL), which aims to jointly learn an optimized graph structure and corresponding representations. Towards this end, in the presented survey, we broadly review recent progress of GSL methods for learning robust representations. Specifically, we first formulate a general paradigm of GSL, and then review state-of-the-art methods classified by how they model graph structures, followed by applications that incorporate the idea of GSL in other graph tasks. Finally, we point out some issues in current studies and discuss future directions.
Current deep learning research is dominated by benchmark evaluation. A method is regarded as favorable if it empirically performs well on the dedicated test set. This mentality is seamlessly reflected in the resurfacing area of continual learning, where consecutively arriving sets of benchmark data are investigated. The core challenge is framed as protecting previously acquired representations from being catastrophically forgotten due to the iterative parameter updates. However, comparison of individual methods is nevertheless treated in isolation from real world application and typically judged by monitoring accumulated test set performance. The closed world assumption remains predominant. It is assumed that during deployment a model is guaranteed to encounter data that stems from the same distribution as used for training. This poses a massive challenge as neural networks are well known to provide overconfident false predictions on unknown instances and break down in the face of corrupted data. In this work we argue that notable lessons from open set recognition, the identification of statistically deviating data outside of the observed dataset, and the adjacent field of active learning, where data is incrementally queried such that the expected performance gain is maximized, are frequently overlooked in the deep learning era. Based on these forgotten lessons, we propose a consolidated view to bridge continual learning, active learning and open set recognition in deep neural networks. Our results show that this not only benefits each individual paradigm, but highlights the natural synergies in a common framework. We empirically demonstrate improvements when alleviating catastrophic forgetting, querying data in active learning, selecting task orders, while exhibiting robust open world application where previously proposed methods fail.