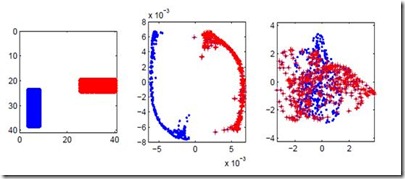
In this paper we study the statistical properties of Principal Components Regression with Laplacian Eigenmaps (PCR-LE), a method for nonparametric regression based on Laplacian Eigenmaps (LE). PCR-LE works by projecting a vector of observed responses ${\bf Y} = (Y_1,\ldots,Y_n)$ onto a subspace spanned by certain eigenvectors of a neighborhood graph Laplacian. We show that PCR-LE achieves minimax rates of convergence for random design regression over Sobolev spaces. Under sufficient smoothness conditions on the design density $p$, PCR-LE achieves the optimal rates for both estimation (where the optimal rate in squared $L^2$ norm is known to be $n^{-2s/(2s + d)}$) and goodness-of-fit testing ($n^{-4s/(4s + d)}$). We also show that PCR-LE is \emph{manifold adaptive}: that is, we consider the situation where the design is supported on a manifold of small intrinsic dimension $m$, and give upper bounds establishing that PCR-LE achieves the faster minimax estimation ($n^{-2s/(2s + m)}$) and testing ($n^{-4s/(4s + m)}$) rates of convergence. Interestingly, these rates are almost always much faster than the known rates of convergence of graph Laplacian eigenvectors to their population-level limits; in other words, for this problem regression with estimated features appears to be much easier, statistically speaking, than estimating the features itself. We support these theoretical results with empirical evidence.
相關內容
Random forests are a widely used machine learning algorithm, but their computational efficiency is undermined when applied to large-scale datasets with numerous instances and useless features. Herein, we propose a nonparametric feature selection algorithm that incorporates random forests and deep neural networks, and its theoretical properties are also investigated under regularity conditions. Using different synthetic models and a real-world example, we demonstrate the advantage of the proposed algorithm over other alternatives in terms of identifying useful features, avoiding useless ones, and the computation efficiency. Although the algorithm is proposed using standard random forests, it can be widely adapted to other machine learning algorithms, as long as features can be sorted accordingly.
In this paper, we study a non-local approximation of the time-dependent (local) Eikonal equation with Dirichlet-type boundary conditions, where the kernel in the non-local problem is properly scaled. Based on the theory of viscosity solutions, we prove existence and uniqueness of the viscosity solutions of both the local and non-local problems, as well as regularity properties of these solutions in time and space. We then derive error bounds between the solution to the non-local problem and that of the local one, both in continuous-time and Backward Euler time discretization. We then turn to studying continuum limits of non-local problems defined on random weighted graphs with $n$ vertices. In particular, we establish that if the kernel scale parameter decreases at an appropriate rate as $n$ grows, then almost surely, the solution of the problem on graphs converges uniformly to the viscosity solution of the local problem as the time step vanishes and the number vertices $n$ grows large.
A Regret Minimizing Set (RMS) is a useful concept in which a smaller subset of a database is selected while mostly preserving the best scores along every possible utility function. In this paper, we study the $k$-Regret Minimizing Sets ($k$-RMS) and Average Regret Minimizing Sets (ARMS) problems. $k$-RMS selects $r$ records from a database such that the maximum regret ratio between the $k$-th best score in the database and the best score in the selected records for any possible utility function is minimized. Meanwhile, ARMS minimizes the average of this ratio within a distribution of utility functions. Particularly, we study approximation algorithms for $k$-RMS and ARMS from the perspective of approximating the happiness ratio, which is equivalent to one minus the regret ratio. In this paper, we show that the problem of approximating the happiness of a $k$-RMS within any finite factor is NP-Hard when the dimensionality of the database is unconstrained and extend the result to an inapproximability proof for the regret. We then provide approximation algorithms for approximating the happiness of ARMS with better approximation ratios and time complexities than known algorithms for approximating the regret. We further provide dataset reduction schemes which can be used to reduce the runtime of existing heuristic based algorithms, as well as to derive polynomial-time approximation schemes for $k$-RMS when dimensionality is fixed. Finally, we provide experimental validation.
The commonly quoted error rates for QMC integration with an infinite low discrepancy sequence is $O(n^{-1}\log(n)^r)$ with $r=d$ for extensible sequences and $r=d-1$ otherwise. Such rates hold uniformly over all $d$ dimensional integrands of Hardy-Krause variation one when using $n$ evaluation points. Implicit in those bounds is that for any sequence of QMC points, the integrand can be chosen to depend on $n$. In this paper we show that rates with any $r<(d-1)/2$ can hold when $f$ is held fixed as $n\to\infty$. This is accomplished following a suggestion of Erich Novak to use some unpublished results of Trojan from the 1980s as given in the information based complexity monograph of Traub, Wasilkowski and Wo\'zniakowski. The proof is made by applying a technique of Roth with the theorem of Trojan. The proof is non constructive and we do not know of any integrand of bounded variation in the sense of Hardy and Krause for which the QMC error exceeds $(\log n)^{1+\epsilon}/n$ for infinitely many $n$ when using a digital sequence such as one of Sobol's. An empirical search when $d=2$ for integrands designed to exploit known weaknesses in certain point sets showed no evidence that $r>1$ is needed. An example with $d=3$ and $n$ up to $2^{100}$ might possibly require $r>1$.
A connected dominating set is a widely adopted model for the virtual backbone of a wireless sensor network. In this paper, we design an evolutionary algorithm for the minimum connected dominating set problem (MinCDS), whose performance is theoretically guaranteed in terms of both computation time and approximation ratio. Given a connected graph $G=(V,E)$, a connected dominating set (CDS) is a subset $C\subseteq V$ such that every vertex in $V\setminus C$ has a neighbor in $C$, and the subgraph of $G$ induced by $C$ is connected. The goal of MinCDS is to find a CDS of $G$ with the minimum cardinality. We show that our evolutionary algorithm can find a CDS in expected $O(n^3)$ time which approximates the optimal value within factor $(2+\ln\Delta)$, where $n$ and $\Delta$ are the number of vertices and the maximum degree of graph $G$, respectively.
The Gromov-Hausdorff distance $(d_{GH})$ proves to be a useful distance measure between shapes. In order to approximate $d_{GH}$ for compact subsets $X,Y\subset\mathbb{R}^d$, we look into its relationship with $d_{H,iso}$, the infimum Hausdorff distance under Euclidean isometries. As already known for dimension $d\geq 2$, the $d_{H,iso}$ cannot be bounded above by a constant factor times $d_{GH}$. For $d=1$, however, we prove that $d_{H,iso}\leq\frac{5}{4}d_{GH}$. We also show that the bound is tight. In effect, this gives rise to an $O(n\log{n})$-time algorithm to approximate $d_{GH}$ with an approximation factor of $\left(1+\frac{1}{4}\right)$.
We study the problem of learning in the stochastic shortest path (SSP) setting, where an agent seeks to minimize the expected cost accumulated before reaching a goal state. We design a novel model-based algorithm EB-SSP that carefully skews the empirical transitions and perturbs the empirical costs with an exploration bonus to guarantee both optimism and convergence of the associated value iteration scheme. We prove that EB-SSP achieves the minimax regret rate $\widetilde{O}(B_{\star} \sqrt{S A K})$, where $K$ is the number of episodes, $S$ is the number of states, $A$ is the number of actions and $B_{\star}$ bounds the expected cumulative cost of the optimal policy from any state, thus closing the gap with the lower bound. Interestingly, EB-SSP obtains this result while being parameter-free, i.e., it does not require any prior knowledge of $B_{\star}$, nor of $T_{\star}$ which bounds the expected time-to-goal of the optimal policy from any state. Furthermore, we illustrate various cases (e.g., positive costs, or general costs when an order-accurate estimate of $T_{\star}$ is available) where the regret only contains a logarithmic dependence on $T_{\star}$, thus yielding the first horizon-free regret bound beyond the finite-horizon MDP setting.
Sampling methods (e.g., node-wise, layer-wise, or subgraph) has become an indispensable strategy to speed up training large-scale Graph Neural Networks (GNNs). However, existing sampling methods are mostly based on the graph structural information and ignore the dynamicity of optimization, which leads to high variance in estimating the stochastic gradients. The high variance issue can be very pronounced in extremely large graphs, where it results in slow convergence and poor generalization. In this paper, we theoretically analyze the variance of sampling methods and show that, due to the composite structure of empirical risk, the variance of any sampling method can be decomposed into \textit{embedding approximation variance} in the forward stage and \textit{stochastic gradient variance} in the backward stage that necessities mitigating both types of variance to obtain faster convergence rate. We propose a decoupled variance reduction strategy that employs (approximate) gradient information to adaptively sample nodes with minimal variance, and explicitly reduces the variance introduced by embedding approximation. We show theoretically and empirically that the proposed method, even with smaller mini-batch sizes, enjoys a faster convergence rate and entails a better generalization compared to the existing methods.
In this work, we consider the distributed optimization of non-smooth convex functions using a network of computing units. We investigate this problem under two regularity assumptions: (1) the Lipschitz continuity of the global objective function, and (2) the Lipschitz continuity of local individual functions. Under the local regularity assumption, we provide the first optimal first-order decentralized algorithm called multi-step primal-dual (MSPD) and its corresponding optimal convergence rate. A notable aspect of this result is that, for non-smooth functions, while the dominant term of the error is in $O(1/\sqrt{t})$, the structure of the communication network only impacts a second-order term in $O(1/t)$, where $t$ is time. In other words, the error due to limits in communication resources decreases at a fast rate even in the case of non-strongly-convex objective functions. Under the global regularity assumption, we provide a simple yet efficient algorithm called distributed randomized smoothing (DRS) based on a local smoothing of the objective function, and show that DRS is within a $d^{1/4}$ multiplicative factor of the optimal convergence rate, where $d$ is the underlying dimension.
Topic models are one of the most frequently used models in machine learning due to its high interpretability and modular structure. However extending the model to include supervisory signal, incorporate pre-trained word embedding vectors and add nonlinear output function to the model is not an easy task because one has to resort to highly intricate approximate inference procedure. In this paper, we show that topic models could be viewed as performing a neighborhood aggregation algorithm where the messages are passed through a network defined over words. Under the network view of topic models, nodes corresponds to words in a document and edges correspond to either a relationship describing co-occurring words in a document or a relationship describing same word in the corpus. The network view allows us to extend the model to include supervisory signals, incorporate pre-trained word embedding vectors and add nonlinear output function to the model in a simple manner. Moreover, we describe a simple way to train the model that is well suited in a semi-supervised setting where we only have supervisory signals for some portion of the corpus and the goal is to improve prediction performance in the held-out data. Through careful experiments we show that our approach outperforms state-of-the-art supervised Latent Dirichlet Allocation implementation in both held-out document classification tasks and topic coherence.