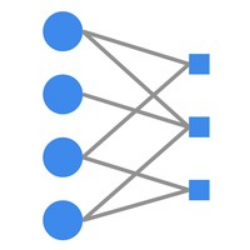
We present a new algorithm for amortized inference in sparse probabilistic graphical models (PGMs), which we call $\Delta$-amortized inference ($\Delta$-AI). Our approach is based on the observation that when the sampling of variables in a PGM is seen as a sequence of actions taken by an agent, sparsity of the PGM enables local credit assignment in the agent's policy learning objective. This yields a local constraint that can be turned into a local loss in the style of generative flow networks (GFlowNets) that enables off-policy training but avoids the need to instantiate all the random variables for each parameter update, thus speeding up training considerably. The $\Delta$-AI objective matches the conditional distribution of a variable given its Markov blanket in a tractable learned sampler, which has the structure of a Bayesian network, with the same conditional distribution under the target PGM. As such, the trained sampler recovers marginals and conditional distributions of interest and enables inference of partial subsets of variables. We illustrate $\Delta$-AI's effectiveness for sampling from synthetic PGMs and training latent variable models with sparse factor structure.
相關內容
Let $S$ be a set of $n$ points in general position in $\mathbb{R}^d$. The order-$k$ Voronoi diagram of $S$, $V_k(S)$, is a subdivision of $\mathbb{R}^d$ into cells whose points have the same $k$ nearest points of $S$. Sibson, in his seminal paper from 1980 (A vector identity for the Dirichlet tessellation), gives a formula to express a point $Q$ of $S$ as a convex combination of other points of $S$ by using ratios of volumes of the intersection of cells of $V_2(S)$ and the cell of $Q$ in $V_1(S)$. The natural neighbour interpolation method is based on Sibson's formula. We generalize his result to express $Q$ as a convex combination of other points of $S$ by using ratios of volumes from Voronoi diagrams of any given order.
Let $SGL_n(\mathbb{F}_2)$ be the set of all invertible $n\times n$ symmetric matrices over the binary field $\mathbb{F}_2$. Let $\Gamma_n$ be the graph with the vertex set $SGL_n(\mathbb{F}_2)$ where a pair of matrices $\{A,B\}$ form an edge if and only if $\textrm{rank}(A-B)=1$. In particular, $\Gamma_3$ is the well-known Coxeter graph. The distance function $d(A,B)$ in $\Gamma_n$ is described for all matrices $A,B\in SGL_n(\mathbb{F}_2)$. The diameter of $\Gamma_n$ is computed. For odd $n\geq 3$, it is shown that each matrix $A\in SGL_n(\mathbb{F}_2)$ such that $d(A,I)=\frac{n+5}{2}$ and $\textrm{rank}(A-I)=\frac{n+1}{2}$ where $I$ is the identity matrix induces a self-dual code in $\mathbb{F}_2^{n+1}$. Conversely, each self-dual code $C$ induces a family ${\cal F}_C$ of such matrices $A$. The families given by distinct self-dual codes are disjoint. The identification $C\leftrightarrow {\cal F}_C$ provides a graph theoretical description of self-dual codes. A result of Janusz (2007) is reproved and strengthened by showing that the orthogonal group ${\cal O}_n(\mathbb{F}_2)$ acts transitively on the set of all self-dual codes in $\mathbb{F}_2^{n+1}$.
We prove that the degree 4 sum-of-squares (SOS) relaxation of the clique number of the Paley graph on a prime number $p$ of vertices has value at least $\Omega(p^{1/3})$. This is in contrast to the widely believed conjecture that the actual clique number of the Paley graph is $O(\mathrm{polylog}(p))$. Our result may be viewed as a derandomization of that of Deshpande and Montanari (2015), who showed the same lower bound (up to $\mathrm{polylog}(p)$ terms) with high probability for the Erd\H{o}s-R\'{e}nyi random graph on $p$ vertices, whose clique number is with high probability $O(\log(p))$. We also show that our lower bound is optimal for the Feige-Krauthgamer construction of pseudomoments, derandomizing an argument of Kelner. Finally, we present numerical experiments indicating that the value of the degree 4 SOS relaxation of the Paley graph may scale as $O(p^{1/2 - \epsilon})$ for some $\epsilon > 0$, and give a matrix norm calculation indicating that the pseudocalibration proof strategy for SOS lower bounds for random graphs will not immediately transfer to the Paley graph. Taken together, our results suggest that degree 4 SOS may break the "$\sqrt{p}$ barrier" for upper bounds on the clique number of Paley graphs, but prove that it can at best improve the exponent from $1/2$ to $1/3$.
The covXtreme software provides functionality for estimation of marginal and conditional extreme value models, non-stationary with respect to covariates, and environmental design contours. Generalised Pareto (GP) marginal models of peaks over threshold are estimated, using a piecewise-constant representation for the variation of GP threshold and scale parameters on the (potentially multidimensional) covariate domain of interest. The conditional variation of one or more associated variates, given a large value of a single conditioning variate, is described using the conditional extremes model of Heffernan and Tawn (2004), the slope term of which is also assumed to vary in a piecewise constant manner with covariates. Optimal smoothness of marginal and conditional extreme value model parameters with respect to covariates is estimated using cross-validated roughness-penalised maximum likelihood estimation. Uncertainties in model parameter estimates due to marginal and conditional extreme value threshold choice, and sample size, are quantified using a bootstrap resampling scheme. Estimates of environmental contours using various schemes, including the direct sampling approach of Huseby et al. 2013, are calculated by simulation or numerical integration under fitted models. The software was developed in MATLAB for metocean applications, but is applicable generally to multivariate samples of peaks over threshold. The software and case study data can be downloaded from GitHub, with an accompanying user guide.
We present a generic algorithm for scoring pose estimation methods that rely on single image semantic analysis. The algorithm employs a lightweight putative shape representation using a combination of multiple Gaussian Processes. Each Gaussian Process (GP) yields distance normal distributions from multiple reference points in the object's coordinate system to its surface, thus providing a geometric evaluation framework for scoring predicted poses. Our confidence measure comprises the average mixture probability of pixel back-projections onto the shape template. In the reported experiments, we compare the accuracy of our GP based representation of objects versus the actual geometric models and demonstrate the ability of our method to capture the influence of outliers as opposed to the corresponding intrinsic measures that ship with the segmentation and pose estimation methods.
We investigate the proof theory of regular expressions with fixed points, construed as a notation for (omega-)context-free grammars. Starting with a hypersequential system for regular expressions due to Das and Pous, we define its extension by least fixed points and prove soundness and completeness of its non-wellfounded proofs for the standard language model. From here we apply proof-theoretic techniques to recover an infinitary axiomatisation of the resulting equational theory, complete for inclusions of context-free languages. Finally, we extend our syntax by greatest fixed points, now computing omega-context-free languages. We show the soundness and completeness of the corresponding system using a mixture of proof-theoretic and game-theoretic techniques.
High-dimensional linear models have been widely studied, but the developments in high-dimensional generalized linear models, or GLMs, have been slower. In this paper, we propose an empirical or data-driven prior leading to an empirical Bayes posterior distribution which can be used for estimation of and inference on the coefficient vector in a high-dimensional GLM, as well as for variable selection. We prove that our proposed posterior concentrates around the true/sparse coefficient vector at the optimal rate, provide conditions under which the posterior can achieve variable selection consistency, and prove a Bernstein--von Mises theorem that implies asymptotically valid uncertainty quantification. Computation of the proposed empirical Bayes posterior is simple and efficient, and is shown to perform well in simulations compared to existing Bayesian and non-Bayesian methods in terms of estimation and variable selection.
The implication problem for conditional independence (CI) asks whether the fact that a probability distribution obeys a given finite set of CI relations implies that a further CI statement also holds in this distribution. This problem has a long and fascinating history, cumulating in positive results about implications now known as the semigraphoid axioms as well as impossibility results about a general finite characterization of CI implications. Motivated by violation of faithfulness assumptions in causal discovery, we study the implication problem in the special setting where the CI relations are obtained from a directed acyclic graphical (DAG) model along with one additional CI statement. Focusing on the Gaussian case, we give a complete characterization of when such an implication is graphical by using algebraic techniques. Moreover, prompted by the relevance of strong faithfulness in statistical guarantees for causal discovery algorithms, we give a graphical solution for an approximate CI implication problem, in which we ask whether small values of one additional partial correlation entail small values for yet a further partial correlation.
This is a simplification of a previous version of this ArXiv note. We present an example of a function $f$ from $\{-1,1\}^n$ to the unit sphere in $\mathbb{C}$ with influence bounded by $1$ and entropy of $|\hat f|^2$ larger than $\frac12\log n$.
Consider the problem of predicting the next symbol given a sample path of length n, whose joint distribution belongs to a distribution class that may have long-term memory. The goal is to compete with the conditional predictor that knows the true model. For both hidden Markov models (HMMs) and renewal processes, we determine the optimal prediction risk in Kullback- Leibler divergence up to universal constant factors. Extending existing results in finite-order Markov models [HJW23] and drawing ideas from universal compression, the proposed estimator has a prediction risk bounded by redundancy of the distribution class and a memory term that accounts for the long-range dependency of the model. Notably, for HMMs with bounded state and observation spaces, a polynomial-time estimator based on dynamic programming is shown to achieve the optimal prediction risk {\Theta}(log n/n); prior to this work, the only known result of this type is O(1/log n) obtained using Markov approximation [Sha+18]. Matching minimax lower bounds are obtained by making connections to redundancy and mutual information via a reduction argument.