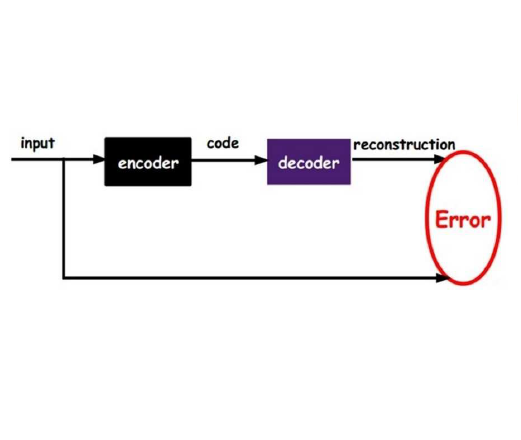
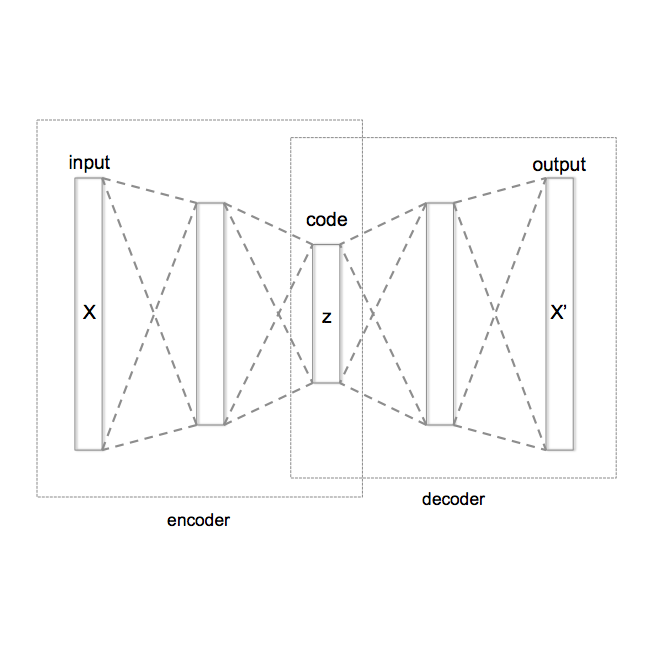
Many real-world processes have complex tail dependence structures that cannot be characterized using classical Gaussian processes. More flexible spatial extremes models exhibit appealing extremal dependence properties but are often exceedingly prohibitive to fit and simulate from in high dimensions. In this paper, we develop a new spatial extremes model that has flexible and non-stationary dependence properties, and we integrate it in the encoding-decoding structure of a variational autoencoder (XVAE), whose parameters are estimated via variational Bayes combined with deep learning. The XVAE can be used as a spatio-temporal emulator that characterizes the distribution of potential mechanistic model output states and produces outputs that have the same statistical properties as the inputs, especially in the tail. As an aside, our approach also provides a novel way of making fast inference with complex extreme-value processes. Through extensive simulation studies, we show that our XVAE is substantially more time-efficient than traditional Bayesian inference while also outperforming many spatial extremes models with a stationary dependence structure. To further demonstrate the computational power of the XVAE, we analyze a high-resolution satellite-derived dataset of sea surface temperature in the Red Sea, which includes 30 years of daily measurements at 16703 grid cells. We find that the extremal dependence strength is weaker in the interior of Red Sea and it has decreased slightly over time.
相關內容
To form precipitation datasets that are accurate and, at the same time, have high spatial densities, data from satellites and gauges are often merged in the literature. However, uncertainty estimates for the data acquired in this manner are scarcely provided, although the importance of uncertainty quantification in predictive modelling is widely recognized. Furthermore, the benefits that machine learning can bring to the task of providing such estimates have not been broadly realized and properly explored through benchmark experiments. The present study aims at filling in this specific gap by conducting the first benchmark tests on the topic. On a large dataset that comprises 15-year-long monthly data spanning across the contiguous United States, we extensively compared six learners that are, by their construction, appropriate for predictive uncertainty quantification. These are the quantile regression (QR), quantile regression forests (QRF), generalized random forests (GRF), gradient boosting machines (GBM), light gradient boosting machines (LightGBM) and quantile regression neural networks (QRNN). The comparison referred to the competence of the learners in issuing predictive quantiles at nine levels that facilitate a good approximation of the entire predictive probability distribution, and was primarily based on the quantile and continuous ranked probability skill scores. Three types of predictor variables (i.e., satellite precipitation variables, distances between a point of interest and satellite grid points, and elevation at a point of interest) were used in the comparison and were additionally compared with each other. This additional comparison was based on the explainable machine learning concept of feature importance. The results suggest that the order from the best to the worst of the learners for the task investigated is the following: LightGBM, QRF, GRF, GBM, QRNN and QR...
Electrodermal activity (EDA) is considered a standard marker of sympathetic activity. However, traditional EDA measurement requires electrodes in steady contact with the skin. Can sympathetic arousal be measured using only an optical sensor, such as an RGB camera? This paper presents a novel approach to infer sympathetic arousal by measuring the peripheral blood flow on the face or hand optically. We contribute a self-recorded dataset of 21 participants, comprising synchronized videos of participants' faces and palms and gold-standard EDA and photoplethysmography (PPG) signals. Our results show that we can measure peripheral sympathetic responses that closely correlate with the ground truth EDA. We obtain median correlations of 0.57 to 0.63 between our inferred signals and the ground truth EDA using only videos of the participants' palms or foreheads or PPG signals from the foreheads or fingers. We also show that sympathetic arousal is best inferred from the forehead, finger, or palm.
Topological signal processing (TSP) over simplicial complexes typically assumes observations associated with the simplicial complexes are real scalars. In this paper, we develop TSP theories for the case where observations belong to general abelian groups, including function spaces that are commonly used to represent time-varying signals. Our approach generalizes the Hodge decomposition and allows for signal processing tasks to be performed on these more complex observations. We propose a unified and flexible framework for TSP that expands its applicability to a wider range of signal processing applications. Numerical results demonstrate the effectiveness of this approach and provide a foundation for future research in this area.
Numerical simulations of kinetic problems can become prohibitively expensive due to their large memory footprint and computational costs. A method that has proven to successfully reduce these costs is the dynamical low-rank approximation (DLRA). One key question when using DLRA methods is the construction of robust time integrators that preserve the invariances and associated conservation laws of the original problem. In this work, we demonstrate that the augmented basis update & Galerkin integrator (BUG) preserves solution invariances and the associated conservation laws when using a conservative truncation step and an appropriate time and space discretization. We present numerical comparisons to existing conservative integrators and discuss advantages and disadvantages
This study compares the performance of (1) fine-tuned models and (2) extremely large language models on the task of check-worthy claim detection. For the purpose of the comparison we composed a multilingual and multi-topical dataset comprising texts of various sources and styles. Building on this, we performed a benchmark analysis to determine the most general multilingual and multi-topical claim detector. We chose three state-of-the-art models in the check-worthy claim detection task and fine-tuned them. Furthermore, we selected three state-of-the-art extremely large language models without any fine-tuning. We made modifications to the models to adapt them for multilingual settings and through extensive experimentation and evaluation. We assessed the performance of all the models in terms of accuracy, recall, and F1-score in in-domain and cross-domain scenarios. Our results demonstrate that despite the technological progress in the area of natural language processing, the models fine-tuned for the task of check-worthy claim detection still outperform the zero-shot approaches in a cross-domain settings.
The consistency of the maximum likelihood estimator for mixtures of elliptically-symmetric distributions for estimating its population version is shown, where the underlying distribution $P$ is nonparametric and does not necessarily belong to the class of mixtures on which the estimator is based. In a situation where $P$ is a mixture of well enough separated but nonparametric distributions it is shown that the components of the population version of the estimator correspond to the well separated components of $P$. This provides some theoretical justification for the use of such estimators for cluster analysis in case that $P$ has well separated subpopulations even if these subpopulations differ from what the mixture model assumes.
Solutions to many important partial differential equations satisfy bounds constraints, but approximations computed by finite element or finite difference methods typically fail to respect the same conditions. Chang and Nakshatrala enforce such bounds in finite element methods through the solution of variational inequalities rather than linear variational problems. Here, we provide a theoretical justification for this method, including higher-order discretizations. We prove an abstract best approximation result for the linear variational inequality and estimates showing that bounds-constrained polynomials provide comparable approximation power to standard spaces. For any unconstrained approximation to a function, there exists a constrained approximation which is comparable in the $W^{1,p}$ norm. In practice, one cannot efficiently represent and manipulate the entire family of bounds-constrained polynomials, but applying bounds constraints to the coefficients of a polynomial in the Bernstein basis guarantees those constraints on the polynomial. Although our theoretical results do not guaruntee high accuracy for this subset of bounds-constrained polynomials, numerical results indicate optimal orders of accuracy for smooth solutions and sharp resolution of features in convection-diffusion problems, all subject to bounds constraints.
Chaotic systems make long-horizon forecasts difficult because small perturbations in initial conditions cause trajectories to diverge at an exponential rate. In this setting, neural operators trained to minimize squared error losses, while capable of accurate short-term forecasts, often fail to reproduce statistical or structural properties of the dynamics over longer time horizons and can yield degenerate results. In this paper, we propose an alternative framework designed to preserve invariant measures of chaotic attractors that characterize the time-invariant statistical properties of the dynamics. Specifically, in the multi-environment setting (where each sample trajectory is governed by slightly different dynamics), we consider two novel approaches to training with noisy data. First, we propose a loss based on the optimal transport distance between the observed dynamics and the neural operator outputs. This approach requires expert knowledge of the underlying physics to determine what statistical features should be included in the optimal transport loss. Second, we show that a contrastive learning framework, which does not require any specialized prior knowledge, can preserve statistical properties of the dynamics nearly as well as the optimal transport approach. On a variety of chaotic systems, our method is shown empirically to preserve invariant measures of chaotic attractors.
Generalized linear models (GLMs) are routinely used for modeling relationships between a response variable and a set of covariates. The simple form of a GLM comes with easy interpretability, but also leads to concerns about model misspecification impacting inferential conclusions. A popular semi-parametric solution adopted in the frequentist literature is quasi-likelihood, which improves robustness by only requiring correct specification of the first two moments. We develop a robust approach to Bayesian inference in GLMs through quasi-posterior distributions. We show that quasi-posteriors provide a coherent generalized Bayes inference method, while also approximating so-called coarsened posteriors. In so doing, we obtain new insights into the choice of coarsening parameter. Asymptotically, the quasi-posterior converges in total variation to a normal distribution and has important connections with the loss-likelihood bootstrap posterior. We demonstrate that it is also well-calibrated in terms of frequentist coverage. Moreover, the loss-scale parameter has a clear interpretation as a dispersion, and this leads to a consolidated method of moments estimator.
The development of cubical type theory inspired the idea of "extension types" which has been found to have applications in other type theories that are unrelated to homotopy type theory or cubical type theory. This article describes these applications, including on records, metaprogramming, controlling unfolding, and some more exotic ones.