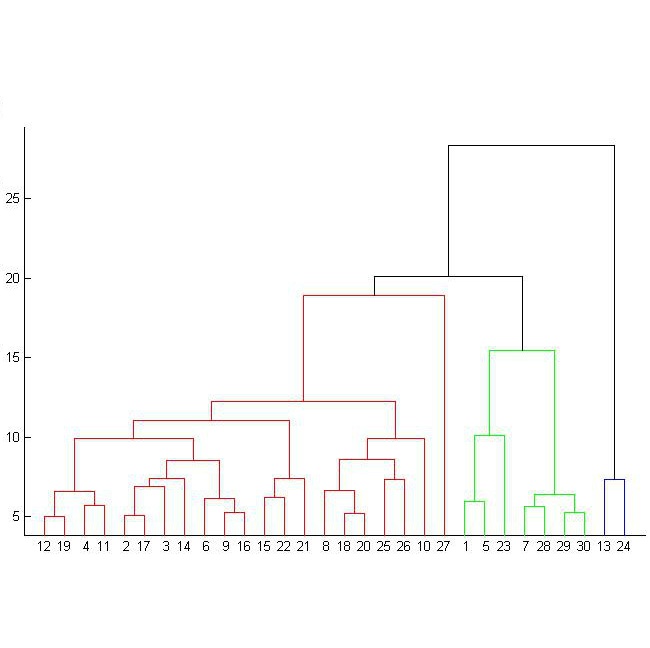
Partial orders and directed acyclic graphs are commonly recurring data structures that arise naturally in numerous domains and applications and are used to represent ordered relations between entities in the domains. Examples are task dependencies in a project plan, transaction order in distributed ledgers and execution sequences of tasks in computer programs, just to mention a few. We study the problem of order preserving hierarchical clustering of this kind of ordered data. That is, if we have $a < b$ in the original data and denote their respective clusters by $[a]$ and $[b]$, then we shall have $[a] < [b]$ in the produced clustering. The clustering is similarity based and uses standard linkage functions, such as single- and complete linkage, and is an extension of classical hierarchical clustering. To achieve this, we define the output from running classical hierarchical clustering on strictly ordered data to be partial dendrograms; sub-trees of classical dendrograms with several connected components. We then construct an embedding of partial dendrograms over a set into the family of ultrametrics over the same set. An optimal hierarchical clustering is defined as the partial dendrogram corresponding to the ultrametric closest to the original dissimilarity measure, measured in the p-norm. Thus, the method is a combination of classical hierarchical clustering and ultrametric fitting. A reference implementation is employed for experiments on both synthetic random data and real world data from a database of machine parts. When compared to existing methods, the experiments show that our method excels both in cluster quality and order preservation.
相關內容
Bayesian Optimization is a sample-efficient black-box optimization procedure that is typically applied to problems with a small number of independent objectives. However, in practice we often wish to optimize objectives defined over many correlated outcomes (or "tasks"). For example, scientists may want to optimize the coverage of a cell tower network across a dense grid of locations. Similarly, engineers may seek to balance the performance of a robot across dozens of different environments via constrained or robust optimization. However, the Gaussian Process (GP) models typically used as probabilistic surrogates for multi-task Bayesian Optimization scale poorly with the number of outcomes, greatly limiting applicability. We devise an efficient technique for exact multi-task GP sampling that combines exploiting Kronecker structure in the covariance matrices with Matheron's identity, allowing us to perform Bayesian Optimization using exact multi-task GP models with tens of thousands of correlated outputs. In doing so, we achieve substantial improvements in sample efficiency compared to existing approaches that only model aggregate functions of the outcomes. We demonstrate how this unlocks a new class of applications for Bayesian Optimization across a range of tasks in science and engineering, including optimizing interference patterns of an optical interferometer with more than 65,000 outputs.
Gathering training data is a key step of any supervised learning task, and it is both critical and expensive. Critical, because the quantity and quality of the training data has a high impact on the performance of the learned function. Expensive, because most practical cases rely on humans-in-the-loop to label the data. The process of determining the correct labels is much more expensive than comparing two items to see whether they belong to the same class. Thus motivated, we propose a setting for training data gathering where the human experts perform the comparatively cheap task of answering pairwise queries, and the computer groups the items into classes (which can be labeled cheaply at the very end of the process). Given the items, we consider two random models for the classes: one where the set partition they form is drawn uniformly, the other one where each item chooses its class independently following a fixed distribution. In the first model, we characterize the algorithms that minimize the average number of queries required to cluster the items and analyze their complexity. In the second model, we analyze a specific algorithm family, propose as a conjecture that they reach the minimum average number of queries and compare their performance to a random approach. We also propose solutions to handle errors or inconsistencies in the experts' answers.
Plotting is a tile-matching puzzle video game published by Taito in 1989. Its objective is to reduce a given grid of coloured blocks down to a goal number or fewer. This is achieved by the avatar character repeatedly shooting the block it holds into the grid. Plotting is an example of a planning problem: given a model of the environment, a planning problem asks us to find a sequence of actions that can lead from an initial state of the environment to a given goal state while respecting some constraints. The key difficulty in modelling Plotting is in capturing the way the puzzle state changes after each shot. A single shot can affect multiple tiles directly, and the grid is affected by gravity so numerous other tiles can be affected indirectly. We present and evaluate a constraint model of the Plotting problem that captures this complexity. We also discuss the difficulties and inefficiencies of modelling Plotting in PDDL, the standard language used for input to specialised AI planners. We conclude by arguing that AI planning could benefit from a richer modelling language.
Recent advances in center-based clustering continue to improve upon the drawbacks of Lloyd's celebrated $k$-means algorithm over $60$ years after its introduction. Various methods seek to address poor local minima, sensitivity to outliers, and data that are not well-suited to Euclidean measures of fit, but many are supported largely empirically. Moreover, combining such approaches in a piecemeal manner can result in ad hoc methods, and the limited theoretical results supporting each individual contribution may no longer hold. Toward addressing these issues in a principled way, this paper proposes a cohesive robust framework for center-based clustering under a general class of dissimilarity measures. In particular, we present a rigorous theoretical treatment within a Median-of-Means (MoM) estimation framework, showing that it subsumes several popular $k$-means variants. In addition to unifying existing methods, we derive uniform concentration bounds that complete their analyses, and bridge these results to the MoM framework via Dudley's chaining arguments. Importantly, we neither require any assumptions on the distribution of the outlying observations nor on the relative number of observations $n$ to features $p$. We establish strong consistency and an error rate of $O(n^{-1/2})$ under mild conditions, surpassing the best-known results in the literature. The methods are empirically validated thoroughly on real and synthetic datasets.
Clustering is one of the most fundamental and wide-spread techniques in exploratory data analysis. Yet, the basic approach to clustering has not really changed: a practitioner hand-picks a task-specific clustering loss to optimize and fit the given data to reveal the underlying cluster structure. Some types of losses---such as k-means, or its non-linear version: kernelized k-means (centroid based), and DBSCAN (density based)---are popular choices due to their good empirical performance on a range of applications. Although every so often the clustering output using these standard losses fails to reveal the underlying structure, and the practitioner has to custom-design their own variation. In this work we take an intrinsically different approach to clustering: rather than fitting a dataset to a specific clustering loss, we train a recurrent model that learns how to cluster. The model uses as training pairs examples of datasets (as input) and its corresponding cluster identities (as output). By providing multiple types of training datasets as inputs, our model has the ability to generalize well on unseen datasets (new clustering tasks). Our experiments reveal that by training on simple synthetically generated datasets or on existing real datasets, we can achieve better clustering performance on unseen real-world datasets when compared with standard benchmark clustering techniques. Our meta clustering model works well even for small datasets where the usual deep learning models tend to perform worse.
Graph convolutional networks (GCNs) have been successfully applied in node classification tasks of network mining. However, most of these models based on neighborhood aggregation are usually shallow and lack the "graph pooling" mechanism, which prevents the model from obtaining adequate global information. In order to increase the receptive field, we propose a novel deep Hierarchical Graph Convolutional Network (H-GCN) for semi-supervised node classification. H-GCN first repeatedly aggregates structurally similar nodes to hyper-nodes and then refines the coarsened graph to the original to restore the representation for each node. Instead of merely aggregating one- or two-hop neighborhood information, the proposed coarsening procedure enlarges the receptive field for each node, hence more global information can be captured. The proposed H-GCN model shows strong empirical performance on various public benchmark graph datasets, outperforming state-of-the-art methods and acquiring up to 5.9% performance improvement in terms of accuracy. In addition, when only a few labeled samples are provided, our model gains substantial improvements.
We present a new clustering method in the form of a single clustering equation that is able to directly discover groupings in the data. The main proposition is that the first neighbor of each sample is all one needs to discover large chains and finding the groups in the data. In contrast to most existing clustering algorithms our method does not require any hyper-parameters, distance thresholds and/or the need to specify the number of clusters. The proposed algorithm belongs to the family of hierarchical agglomerative methods. The technique has a very low computational overhead, is easily scalable and applicable to large practical problems. Evaluation on well known datasets from different domains ranging between 1077 and 8.1 million samples shows substantial performance gains when compared to the existing clustering techniques.
Recently, graph neural networks (GNNs) have revolutionized the field of graph representation learning through effectively learned node embeddings, and achieved state-of-the-art results in tasks such as node classification and link prediction. However, current GNN methods are inherently flat and do not learn hierarchical representations of graphs---a limitation that is especially problematic for the task of graph classification, where the goal is to predict the label associated with an entire graph. Here we propose DiffPool, a differentiable graph pooling module that can generate hierarchical representations of graphs and can be combined with various graph neural network architectures in an end-to-end fashion. DiffPool learns a differentiable soft cluster assignment for nodes at each layer of a deep GNN, mapping nodes to a set of clusters, which then form the coarsened input for the next GNN layer. Our experimental results show that combining existing GNN methods with DiffPool yields an average improvement of 5-10% accuracy on graph classification benchmarks, compared to all existing pooling approaches, achieving a new state-of-the-art on four out of five benchmark data sets.
Knowledge Graph Embedding methods aim at representing entities and relations in a knowledge base as points or vectors in a continuous vector space. Several approaches using embeddings have shown promising results on tasks such as link prediction, entity recommendation, question answering, and triplet classification. However, only a few methods can compute low-dimensional embeddings of very large knowledge bases. In this paper, we propose KG2Vec, a novel approach to Knowledge Graph Embedding based on the skip-gram model. Instead of using a predefined scoring function, we learn it relying on Long Short-Term Memories. We evaluated the goodness of our embeddings on knowledge graph completion and show that KG2Vec is comparable to the quality of the scalable state-of-the-art approaches and can process large graphs by parsing more than a hundred million triples in less than 6 hours on common hardware.