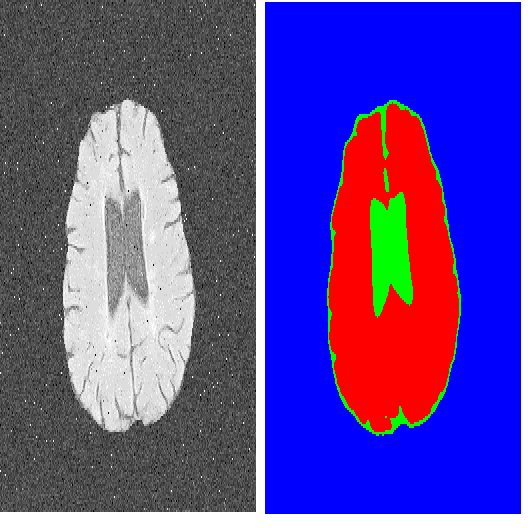
Minimum distance estimation methodology based on empirical distribution function has been popular due to its desirable properties including robustness. Even though the statistical literature is awash with the research on the minimum distance estimation, the most of it is confined to the theoretical findings: only few statisticians conducted research on the application of the method to real world problems. Through this paper, we extend the domain of application of this methodology to various applied fields by providing a solution to a rather challenging and complicated computational problem. The problem this paper tackles is an image segmentation which has been used in various fields. We propose a novel method based on the classical minimum distance estimation theory to solve the image segmentation problem. The performance of the proposed method is then further elevated by integrating it with the "segmenting-together" strategy.
相關內容
We study a fundamental model of online preference aggregation, where an algorithm maintains an ordered list of $n$ elements. An input is a stream of preferred sets $R_1, R_2, \dots, R_t, \dots$. Upon seeing $R_t$ and without knowledge of any future sets, an algorithm has to rerank elements (change the list ordering), so that at least one element of $R_t$ is found near the list front. The incurred cost is a sum of the list update costs (the number of swaps of neighboring list elements) and access costs (position of the first element of $R_t$ on the list). This scenario occurs naturally in applications such as ordering items in an online shop using aggregated preferences of shop customers. The theoretical underpinning of this problem is known as Min-Sum Set Cover. Unlike previous work (Fotakis et al., ICALP 2020, NIPS 2020) that mostly studied the performance of an online algorithm ALG against the static optimal solution (a single optimal list ordering), in this paper, we study an arguably harder variant where the benchmark is the provably stronger optimal dynamic solution OPT (that may also modify the list ordering). In terms of an online shop, this means that the aggregated preferences of its user base evolve with time. We construct a computationally efficient randomized algorithm whose competitive ratio (ALG-to-OPT cost ratio) is $O(r^2)$ and prove the existence of a deterministic $O(r^4)$-competitive algorithm. Here, $r$ is the maximum cardinality of sets $R_t$. This is the first algorithm whose ratio does not depend on $n$: the previously best algorithm for this problem was $O(r^{3/2} \cdot \sqrt{n})$-competitive and $\Omega(r)$ is a lower bound on the performance of any deterministic online algorithm.
Gaussian mixtures are commonly used for modeling heavy-tailed error distributions in robust linear regression. Combining the likelihood of a multivariate robust linear regression model with a standard improper prior distribution yields an analytically intractable posterior distribution that can be sampled using a data augmentation algorithm. When the response matrix has missing entries, there are unique challenges to the application and analysis of the convergence properties of the algorithm. Conditions for geometric ergodicity are provided when the incomplete data have a "monotone" structure. In the absence of a monotone structure, an intermediate imputation step is necessary for implementing the algorithm. In this case, we provide sufficient conditions for the algorithm to be Harris ergodic. Finally, we show that, when there is a monotone structure and intermediate imputation is unnecessary, intermediate imputation slows the convergence of the underlying Monte Carlo Markov chain, while post hoc imputation does not. An R package for the data augmentation algorithm is provided.
Image reconstruction using deep learning algorithms offers improved reconstruction quality and lower reconstruction time than classical compressed sensing and model-based algorithms. Unfortunately, clean and fully sampled ground-truth data to train the deep networks is often unavailable in several applications, restricting the applicability of the above methods. We introduce a novel metric termed the ENsemble Stein's Unbiased Risk Estimate (ENSURE) framework, which can be used to train deep image reconstruction algorithms without fully sampled and noise-free images. The proposed framework is the generalization of the classical SURE and GSURE formulation to the setting where the images are sampled by different measurement operators, chosen randomly from a set. We evaluate the expectation of the GSURE loss functions over the sampling patterns to obtain the ENSURE loss function. We show that this loss is an unbiased estimate for the true mean-square error, which offers a better alternative to GSURE, which only offers an unbiased estimate for the projected error. Our experiments show that the networks trained with this loss function can offer reconstructions comparable to the supervised setting. While we demonstrate this framework in the context of MR image recovery, the ENSURE framework is generally applicable to arbitrary inverse problems.
Significant progress has been made in learning image classification neural networks under long-tail data distribution using robust training algorithms such as data re-sampling, re-weighting, and margin adjustment. Those methods, however, ignore the impact of data imbalance on feature normalization. The dominance of majority classes (head classes) in estimating statistics and affine parameters causes internal covariate shifts within less-frequent categories to be overlooked. To alleviate this challenge, we propose a compound batch normalization method based on a Gaussian mixture. It can model the feature space more comprehensively and reduce the dominance of head classes. In addition, a moving average-based expectation maximization (EM) algorithm is employed to estimate the statistical parameters of multiple Gaussian distributions. However, the EM algorithm is sensitive to initialization and can easily become stuck in local minima where the multiple Gaussian components continue to focus on majority classes. To tackle this issue, we developed a dual-path learning framework that employs class-aware split feature normalization to diversify the estimated Gaussian distributions, allowing the Gaussian components to fit with training samples of less-frequent classes more comprehensively. Extensive experiments on commonly used datasets demonstrated that the proposed method outperforms existing methods on long-tailed image classification.
Multifidelity methods are widely used for estimating quantities of interest (QoI) in computational science by employing numerical simulations of differing costs and accuracies. Many methods approximate numerical-valued statistics that represent only limited information, e.g., scalar statistics, about the QoI. Further quantification of uncertainty, e.g., for risk assessment, failure probabilities, or confidence intervals, requires estimation of the full distributions. In this paper, we generalize the ideas in [Xu et al., SIAM J. Sci. Comput. 44.1 (2022), A150-A175] to develop a multifidelity method that approximates the full distribution of scalar-valued QoI. The main advantage of our approach compared to alternative methods is that we require no particular relationships among the high and lower-fidelity models (e.g. model hierarchy), and we do not assume any knowledge of model statistics including correlations and other cross-model statistics before the procedure starts. Under suitable assumptions in the framework above, we achieve provable 1-Wasserstein metric convergence of an algorithmically constructed distributional emulator via an exploration-exploitation strategy. We also prove that crucial policy actions taken by our algorithm are budget-asymptotically optimal. Numerical experiments are provided to support our theoretical analysis.
Some classical uncertainty quantification problems require the estimation of multiple expectations. Estimating all of them accurately is crucial and can have a major impact on the analysis to perform, and standard existing Monte Carlo methods can be costly to do so. We propose here a new procedure based on importance sampling and control variates for estimating more efficiently multiple expectations with the same sample. We first show that there exists a family of optimal estimators combining both importance sampling and control variates, which however cannot be used in practice because they require the knowledge of the values of the expectations to estimate. Motivated by the form of these optimal estimators and some interesting properties, we therefore propose an adaptive algorithm. The general idea is to adaptively update the parameters of the estimators for approaching the optimal ones. We suggest then a quantitative stopping criterion that exploits the trade-off between approaching these optimal parameters and having a sufficient budget left. This left budget is then used to draw a new independent sample from the final sampling distribution, allowing to get unbiased estimators of the expectations. We show how to apply our procedure to sensitivity analysis, by estimating Sobol' indices and quantifying the impact of the input distributions. Finally, realistic test cases show the practical interest of the proposed algorithm, and its significant improvement over estimating the expectations separately.
The adaptive processing of structured data is a long-standing research topic in machine learning that investigates how to automatically learn a mapping from a structured input to outputs of various nature. Recently, there has been an increasing interest in the adaptive processing of graphs, which led to the development of different neural network-based methodologies. In this thesis, we take a different route and develop a Bayesian Deep Learning framework for graph learning. The dissertation begins with a review of the principles over which most of the methods in the field are built, followed by a study on graph classification reproducibility issues. We then proceed to bridge the basic ideas of deep learning for graphs with the Bayesian world, by building our deep architectures in an incremental fashion. This framework allows us to consider graphs with discrete and continuous edge features, producing unsupervised embeddings rich enough to reach the state of the art on several classification tasks. Our approach is also amenable to a Bayesian nonparametric extension that automatizes the choice of almost all model's hyper-parameters. Two real-world applications demonstrate the efficacy of deep learning for graphs. The first concerns the prediction of information-theoretic quantities for molecular simulations with supervised neural models. After that, we exploit our Bayesian models to solve a malware-classification task while being robust to intra-procedural code obfuscation techniques. We conclude the dissertation with an attempt to blend the best of the neural and Bayesian worlds together. The resulting hybrid model is able to predict multimodal distributions conditioned on input graphs, with the consequent ability to model stochasticity and uncertainty better than most works. Overall, we aim to provide a Bayesian perspective into the articulated research field of deep learning for graphs.
Since deep neural networks were developed, they have made huge contributions to everyday lives. Machine learning provides more rational advice than humans are capable of in almost every aspect of daily life. However, despite this achievement, the design and training of neural networks are still challenging and unpredictable procedures. To lower the technical thresholds for common users, automated hyper-parameter optimization (HPO) has become a popular topic in both academic and industrial areas. This paper provides a review of the most essential topics on HPO. The first section introduces the key hyper-parameters related to model training and structure, and discusses their importance and methods to define the value range. Then, the research focuses on major optimization algorithms and their applicability, covering their efficiency and accuracy especially for deep learning networks. This study next reviews major services and toolkits for HPO, comparing their support for state-of-the-art searching algorithms, feasibility with major deep learning frameworks, and extensibility for new modules designed by users. The paper concludes with problems that exist when HPO is applied to deep learning, a comparison between optimization algorithms, and prominent approaches for model evaluation with limited computational resources.
Modern neural network training relies heavily on data augmentation for improved generalization. After the initial success of label-preserving augmentations, there has been a recent surge of interest in label-perturbing approaches, which combine features and labels across training samples to smooth the learned decision surface. In this paper, we propose a new augmentation method that leverages the first and second moments extracted and re-injected by feature normalization. We replace the moments of the learned features of one training image by those of another, and also interpolate the target labels. As our approach is fast, operates entirely in feature space, and mixes different signals than prior methods, one can effectively combine it with existing augmentation methods. We demonstrate its efficacy across benchmark data sets in computer vision, speech, and natural language processing, where it consistently improves the generalization performance of highly competitive baseline networks.
Image segmentation is an important component of many image understanding systems. It aims to group pixels in a spatially and perceptually coherent manner. Typically, these algorithms have a collection of parameters that control the degree of over-segmentation produced. It still remains a challenge to properly select such parameters for human-like perceptual grouping. In this work, we exploit the diversity of segments produced by different choices of parameters. We scan the segmentation parameter space and generate a collection of image segmentation hypotheses (from highly over-segmented to under-segmented). These are fed into a cost minimization framework that produces the final segmentation by selecting segments that: (1) better describe the natural contours of the image, and (2) are more stable and persistent among all the segmentation hypotheses. We compare our algorithm's performance with state-of-the-art algorithms, showing that we can achieve improved results. We also show that our framework is robust to the choice of segmentation kernel that produces the initial set of hypotheses.