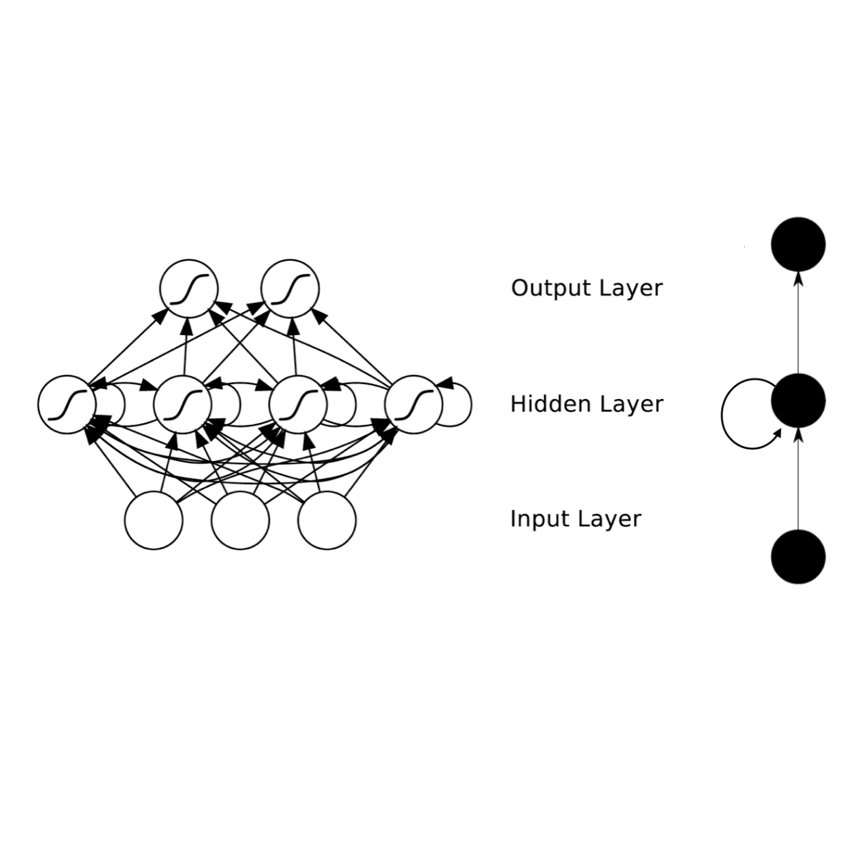
We provide a general framework for studying recurrent neural networks (RNNs) trained by injecting noise into hidden states. Specifically, we consider RNNs that can be viewed as discretizations of stochastic differential equations driven by input data. This framework allows us to study the implicit regularization effect of general noise injection schemes by deriving an approximate explicit regularizer in the small noise regime. We find that, under reasonable assumptions, this implicit regularization promotes flatter minima; it biases towards models with more stable dynamics; and, in classification tasks, it favors models with larger classification margin. Sufficient conditions for global stability are obtained, highlighting the phenomenon of stochastic stabilization, where noise injection can improve stability during training. Our theory is supported by empirical results which demonstrate that the RNNs have improved robustness with respect to various input perturbations.
相關內容
Recurrent neural networks (RNNs) are a popular choice for modeling sequential data. Modern RNN architectures assume constant time intervals between observations. However, in many datasets (e.g. medical records) observation times are irregular and can carry important information. To address this challenge, we propose continuous recurrent units (CRUs) -- a neural architecture that can naturally handle irregular intervals between observations. The CRU assumes a hidden state, which evolves according to a linear stochastic differential equation and is integrated into an encoder-decoder framework. The recursive computations of the CRU can be derived using the continuous-discrete Kalman filter and are in closed form. The resulting recurrent architecture has temporal continuity between hidden states and a gating mechanism that can optimally integrate noisy observations. We derive an efficient parameterization scheme for the CRU that leads to a fast implementation (f-CRU). We empirically study the CRU on a number of challenging datasets and find that it can interpolate irregular time-series better than methods based on neural ordinary differential equations.
Neural Tangent Kernel (NTK) theory is widely used to study the dynamics of infinitely-wide deep neural networks (DNNs) under gradient descent. But do the results for infinitely-wide networks give us hints about the behavior of real finite-width ones? In this paper, we study empirically when NTK theory is valid in practice for fully-connected ReLU and sigmoid DNNs. We find out that whether a network is in the NTK regime depends on the hyperparameters of random initialization and the network's depth. In particular, NTK theory does not explain the behavior of sufficiently deep networks initialized so that their gradients explode as they propagate through the network's layers: the kernel is random at initialization and changes significantly during training in this case, contrary to NTK theory. On the other hand, in the case of vanishing gradients, DNNs are in the the NTK regime but become untrainable rapidly with depth. We also describe a framework to study generalization properties of DNNs, in particular the variance of network's output function, by means of NTK theory and discuss its limits.
The essence of multivariate sequential learning is all about how to extract dependencies in data. These data sets, such as hourly medical records in intensive care units and multi-frequency phonetic time series, often time exhibit not only strong serial dependencies in the individual components (the "marginal" memory) but also non-negligible memories in the cross-sectional dependencies (the "joint" memory). Because of the multivariate complexity in the evolution of the joint distribution that underlies the data generating process, we take a data-driven approach and construct a novel recurrent network architecture, termed Memory-Gated Recurrent Networks (mGRN), with gates explicitly regulating two distinct types of memories: the marginal memory and the joint memory. Through a combination of comprehensive simulation studies and empirical experiments on a range of public datasets, we show that our proposed mGRN architecture consistently outperforms state-of-the-art architectures targeting multivariate time series.
Perturbations targeting the graph structure have proven to be extremely effective in reducing the performance of Graph Neural Networks (GNNs), and traditional defenses such as adversarial training do not seem to be able to improve robustness. This work is motivated by the observation that adversarially injected edges effectively can be viewed as additional samples to a node's neighborhood aggregation function, which results in distorted aggregations accumulating over the layers. Conventional GNN aggregation functions, such as a sum or mean, can be distorted arbitrarily by a single outlier. We propose a robust aggregation function motivated by the field of robust statistics. Our approach exhibits the largest possible breakdown point of 0.5, which means that the bias of the aggregation is bounded as long as the fraction of adversarial edges of a node is less than 50\%. Our novel aggregation function, Soft Medoid, is a fully differentiable generalization of the Medoid and therefore lends itself well for end-to-end deep learning. Equipping a GNN with our aggregation improves the robustness with respect to structure perturbations on Cora ML by a factor of 3 (and 5.5 on Citeseer) and by a factor of 8 for low-degree nodes.
Graph Neural Networks (GNNs) are based on repeated aggregations of information across nodes' neighbors in a graph. However, because common neighbors are shared between different nodes, this leads to repeated and inefficient computations. We propose Hierarchically Aggregated computation Graphs (HAGs), a new GNN graph representation that explicitly avoids redundancy by managing intermediate aggregation results hierarchically, eliminating repeated computations and unnecessary data transfers in GNN training and inference. We introduce an accurate cost function to quantitatively evaluate the runtime performance of different HAGs and use a novel HAG search algorithm to find optimized HAGs. Experiments show that the HAG representation significantly outperforms the standard GNN graph representation by increasing the end-to-end training throughput by up to 2.8x and reducing the aggregations and data transfers in GNN training by up to 6.3x and 5.6x, while maintaining the original model accuracy.
Graph neural networks (GNNs) are a popular class of machine learning models whose major advantage is their ability to incorporate a sparse and discrete dependency structure between data points. Unfortunately, GNNs can only be used when such a graph-structure is available. In practice, however, real-world graphs are often noisy and incomplete or might not be available at all. With this work, we propose to jointly learn the graph structure and the parameters of graph convolutional networks (GCNs) by approximately solving a bilevel program that learns a discrete probability distribution on the edges of the graph. This allows one to apply GCNs not only in scenarios where the given graph is incomplete or corrupted but also in those where a graph is not available. We conduct a series of experiments that analyze the behavior of the proposed method and demonstrate that it outperforms related methods by a significant margin.
Recurrent neural networks (RNNs) provide state-of-the-art performance in processing sequential data but are memory intensive to train, limiting the flexibility of RNN models which can be trained. Reversible RNNs---RNNs for which the hidden-to-hidden transition can be reversed---offer a path to reduce the memory requirements of training, as hidden states need not be stored and instead can be recomputed during backpropagation. We first show that perfectly reversible RNNs, which require no storage of the hidden activations, are fundamentally limited because they cannot forget information from their hidden state. We then provide a scheme for storing a small number of bits in order to allow perfect reversal with forgetting. Our method achieves comparable performance to traditional models while reducing the activation memory cost by a factor of 10--15. We extend our technique to attention-based sequence-to-sequence models, where it maintains performance while reducing activation memory cost by a factor of 5--10 in the encoder, and a factor of 10--15 in the decoder.
Memory-based neural networks model temporal data by leveraging an ability to remember information for long periods. It is unclear, however, whether they also have an ability to perform complex relational reasoning with the information they remember. Here, we first confirm our intuitions that standard memory architectures may struggle at tasks that heavily involve an understanding of the ways in which entities are connected -- i.e., tasks involving relational reasoning. We then improve upon these deficits by using a new memory module -- a \textit{Relational Memory Core} (RMC) -- which employs multi-head dot product attention to allow memories to interact. Finally, we test the RMC on a suite of tasks that may profit from more capable relational reasoning across sequential information, and show large gains in RL domains (e.g. Mini PacMan), program evaluation, and language modeling, achieving state-of-the-art results on the WikiText-103, Project Gutenberg, and GigaWord datasets.
Partially inspired by successful applications of variational recurrent neural networks, we propose a novel variational recurrent neural machine translation (VRNMT) model in this paper. Different from the variational NMT, VRNMT introduces a series of latent random variables to model the translation procedure of a sentence in a generative way, instead of a single latent variable. Specifically, the latent random variables are included into the hidden states of the NMT decoder with elements from the variational autoencoder. In this way, these variables are recurrently generated, which enables them to further capture strong and complex dependencies among the output translations at different timesteps. In order to deal with the challenges in performing efficient posterior inference and large-scale training during the incorporation of latent variables, we build a neural posterior approximator, and equip it with a reparameterization technique to estimate the variational lower bound. Experiments on Chinese-English and English-German translation tasks demonstrate that the proposed model achieves significant improvements over both the conventional and variational NMT models.
Recently, deep learning has achieved very promising results in visual object tracking. Deep neural networks in existing tracking methods require a lot of training data to learn a large number of parameters. However, training data is not sufficient for visual object tracking as annotations of a target object are only available in the first frame of a test sequence. In this paper, we propose to learn hierarchical features for visual object tracking by using tree structure based Recursive Neural Networks (RNN), which have fewer parameters than other deep neural networks, e.g. Convolutional Neural Networks (CNN). First, we learn RNN parameters to discriminate between the target object and background in the first frame of a test sequence. Tree structure over local patches of an exemplar region is randomly generated by using a bottom-up greedy search strategy. Given the learned RNN parameters, we create two dictionaries regarding target regions and corresponding local patches based on the learned hierarchical features from both top and leaf nodes of multiple random trees. In each of the subsequent frames, we conduct sparse dictionary coding on all candidates to select the best candidate as the new target location. In addition, we online update two dictionaries to handle appearance changes of target objects. Experimental results demonstrate that our feature learning algorithm can significantly improve tracking performance on benchmark datasets.