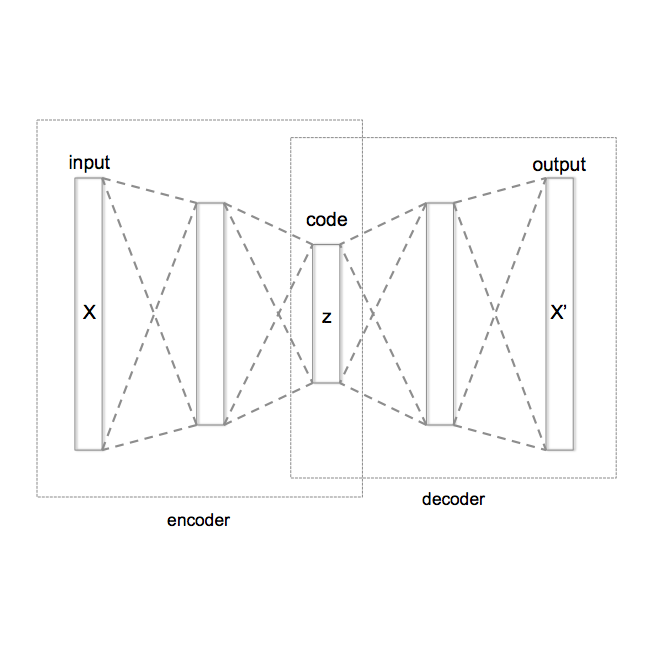
Constrained optimization problems can be difficult because their search spaces have properties not conducive to search, e.g., multimodality, discontinuities, or deception. To address such difficulties, considerable research has been performed on creating novel evolutionary algorithms or specialized genetic operators. However, if the representation that defined the search space could be altered such that it only permitted valid solutions that satisfied the constraints, the task of finding the optimal would be made more feasible without any need for specialized optimization algorithms. We propose the use of a Variational Autoencoder to learn such representations. We present Constrained Optimization in Latent Space (COIL), which uses a VAE to generate a learned latent representation from a dataset comprising samples from the valid region of the search space according to a constraint, thus enabling the optimizer to find the objective in the new space defined by the learned representation. We investigate the value of this approach on different constraint types and for different numbers of variables. We show that, compared to an identical GA using a standard representation, COIL with its learned latent representation can satisfy constraints and find solutions with distance to objective up to two orders of magnitude closer.
相關內容
We introduce a new constrained optimization method for policy gradient reinforcement learning, which uses two trust regions to regulate each policy update. In addition to using the proximity of one single old policy as the first trust region as done by prior works, we propose to form a second trust region through the construction of another virtual policy that represents a wide range of past policies. We then enforce the new policy to stay closer to the virtual policy, which is beneficial in case the old policy performs badly. More importantly, we propose a mechanism to automatically build the virtual policy from a memory buffer of past policies, providing a new capability for dynamically selecting appropriate trust regions during the optimization process. Our proposed method, dubbed as Memory-Constrained Policy Optimization (MCPO), is examined on a diverse suite of environments including robotic locomotion control, navigation with sparse rewards and Atari games, consistently demonstrating competitive performance against recent on-policy constrained policy gradient methods.
We consider the offline constrained reinforcement learning (RL) problem, in which the agent aims to compute a policy that maximizes expected return while satisfying given cost constraints, learning only from a pre-collected dataset. This problem setting is appealing in many real-world scenarios, where direct interaction with the environment is costly or risky, and where the resulting policy should comply with safety constraints. However, it is challenging to compute a policy that guarantees satisfying the cost constraints in the offline RL setting, since the off-policy evaluation inherently has an estimation error. In this paper, we present an offline constrained RL algorithm that optimizes the policy in the space of the stationary distribution. Our algorithm, COptiDICE, directly estimates the stationary distribution corrections of the optimal policy with respect to returns, while constraining the cost upper bound, with the goal of yielding a cost-conservative policy for actual constraint satisfaction. Experimental results show that COptiDICE attains better policies in terms of constraint satisfaction and return-maximization, outperforming baseline algorithms.
We propose an unsupervised method for 3D geometry-aware representation learning of articulated objects. Though photorealistic images of articulated objects can be rendered with explicit pose control through existing 3D neural representations, these methods require ground truth 3D pose and foreground masks for training, which are expensive to obtain. We obviate this need by learning the representations with GAN training. From random poses and latent vectors, the generator is trained to produce realistic images of articulated objects by adversarial training. To avoid a large computational cost for GAN training, we propose an efficient neural representation for articulated objects based on tri-planes and then present a GAN-based framework for its unsupervised training. Experiments demonstrate the efficiency of our method and show that GAN-based training enables learning of controllable 3D representations without supervision.
We give a fast algorithm for sampling uniform solutions of general constraint satisfaction problems (CSPs) in a local lemma regime. The expected running time of our algorithm is near-linear in $n$ and a fixed polynomial in $\Delta$, where $n$ is the number of variables and $\Delta$ is the max degree of constraints. Previously, up to similar conditions, sampling algorithms with running time polynomial in both $n$ and $\Delta$, only existed for the almost atomic case, where each constraint is violated by a small number of forbidden local configurations. Our sampling approach departs from all previous fast algorithms for sampling LLL, which were based on Markov chains. A crucial step of our algorithm is a recursive marginal sampler that is of independent interests. Within a local lemma regime, this marginal sampler can draw a random value for a variable according to its marginal distribution, at a local cost independent of the size of the CSP.
Numerical solution of heterogeneous Helmholtz problems presents various computational challenges, with descriptive theory remaining out of reach for many popular approaches. Robustness and scalability are key for practical and reliable solvers in large-scale applications, especially for large wave number problems. In this work we explore the use of a GenEO-type coarse space to build a two-level additive Schwarz method applicable to highly indefinite Helmholtz problems. Through a range of numerical tests on a 2D model problem, discretised by finite elements on pollution-free meshes, we observe robust convergence, iteration counts that do not increase with the wave number, and good scalability of our approach. We further provide results showing a favourable comparison with the DtN coarse space. Our numerical study shows promise that our solver methodology can be effective for challenging heterogeneous applications.
This paper studies the application of reconfigurable intelligent surface (RIS) to cooperative non-orthogonal multiple access (C-NOMA) networks with simultaneous wireless information and power transfer (SWIPT). We aim for maximizing the rate of the strong user with guaranteed weak user's quality of service (QoS) by jointly optimizing power splitting factors, beamforming coefficients, and RIS reflection coefficients in two transmission phases. The formulated problem is difficult to solve due to its complex and non-convex constraints. To tackle this challenging problem, we first use alternating optimization (AO) framework to transform it into three subproblems, and then use the penalty-based arithmetic-geometric mean approximation (PBAGM) algorithm and the successive convex approximation (SCA)-based method to solve them. Numerical results verify the superiority of the proposed algorithm over the baseline schemes.
Computing a maximum independent set (MaxIS) is a fundamental NP-hard problem in graph theory, which has important applications in a wide spectrum of fields. Since graphs in many applications are changing frequently over time, the problem of maintaining a MaxIS over dynamic graphs has attracted increasing attention over the past few years. Due to the intractability of maintaining an exact MaxIS, this paper aims to develop efficient algorithms that can maintain an approximate MaxIS with an accuracy guarantee theoretically. In particular, we propose a framework that maintains a $(\frac{\Delta}{2} + 1)$-approximate MaxIS over dynamic graphs and prove that it achieves a constant approximation ratio in many real-world networks. To the best of our knowledge, this is the first non-trivial approximability result for the dynamic MaxIS problem. Following the framework, we implement an efficient linear-time dynamic algorithm and a more effective dynamic algorithm with near-linear expected time complexity. Our thorough experiments over real and synthetic graphs demonstrate the effectiveness and efficiency of the proposed algorithms, especially when the graph is highly dynamic.
The numerical solution of singular eigenvalue problems is complicated by the fact that small perturbations of the coefficients may have an arbitrarily bad effect on eigenvalue accuracy. However, it has been known for a long time that such perturbations are exceptional and standard eigenvalue solvers, such as the QZ algorithm, tend to yield good accuracy despite the inevitable presence of roundoff error. Recently, Lotz and Noferini quantified this phenomenon by introducing the concept of $\delta$-weak eigenvalue condition numbers. In this work, we consider singular quadratic eigenvalue problems and two popular linearizations. Our results show that a correctly chosen linearization increases $\delta$-weak eigenvalue condition numbers only marginally, justifying the use of these linearizations in numerical solvers also in the singular case. We propose a very simple but often effective algorithm for computing well-conditioned eigenvalues of a singular quadratic eigenvalue problems by adding small random perturbations to the coefficients. We prove that the eigenvalue condition number is, with high probability, a reliable criterion for detecting and excluding spurious eigenvalues created from the singular part.
The adaptive processing of structured data is a long-standing research topic in machine learning that investigates how to automatically learn a mapping from a structured input to outputs of various nature. Recently, there has been an increasing interest in the adaptive processing of graphs, which led to the development of different neural network-based methodologies. In this thesis, we take a different route and develop a Bayesian Deep Learning framework for graph learning. The dissertation begins with a review of the principles over which most of the methods in the field are built, followed by a study on graph classification reproducibility issues. We then proceed to bridge the basic ideas of deep learning for graphs with the Bayesian world, by building our deep architectures in an incremental fashion. This framework allows us to consider graphs with discrete and continuous edge features, producing unsupervised embeddings rich enough to reach the state of the art on several classification tasks. Our approach is also amenable to a Bayesian nonparametric extension that automatizes the choice of almost all model's hyper-parameters. Two real-world applications demonstrate the efficacy of deep learning for graphs. The first concerns the prediction of information-theoretic quantities for molecular simulations with supervised neural models. After that, we exploit our Bayesian models to solve a malware-classification task while being robust to intra-procedural code obfuscation techniques. We conclude the dissertation with an attempt to blend the best of the neural and Bayesian worlds together. The resulting hybrid model is able to predict multimodal distributions conditioned on input graphs, with the consequent ability to model stochasticity and uncertainty better than most works. Overall, we aim to provide a Bayesian perspective into the articulated research field of deep learning for graphs.
Self-supervised learning has been widely used to obtain transferrable representations from unlabeled images. Especially, recent contrastive learning methods have shown impressive performances on downstream image classification tasks. While these contrastive methods mainly focus on generating invariant global representations at the image-level under semantic-preserving transformations, they are prone to overlook spatial consistency of local representations and therefore have a limitation in pretraining for localization tasks such as object detection and instance segmentation. Moreover, aggressively cropped views used in existing contrastive methods can minimize representation distances between the semantically different regions of a single image. In this paper, we propose a spatially consistent representation learning algorithm (SCRL) for multi-object and location-specific tasks. In particular, we devise a novel self-supervised objective that tries to produce coherent spatial representations of a randomly cropped local region according to geometric translations and zooming operations. On various downstream localization tasks with benchmark datasets, the proposed SCRL shows significant performance improvements over the image-level supervised pretraining as well as the state-of-the-art self-supervised learning methods.